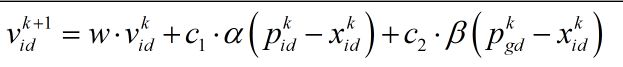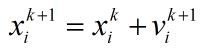PSO粒子群算法（python3.6实现与详解）

1、

学习代码源自：用python3实现粒子群优化算法（PSO）-by雨破尘

参考博文：[MATLAB] 经典智能算法1：粒子群优化算法PSO 

                  python粒子群算法的实现 by-winycg    此篇强推

                  粒子群优化算法(PSO) by森先生

2、算法思想

粒子运动思想（即鸟群捕食运动），同样是通过适应度来评价解好坏。区域里只有一块食物，每一只鸟并不知道食物在哪里，只知道距离食物有多远，最简单有效的就是搜寻离食物最近的鸟的周围区域。这里，每个优化问题的解都是搜索空间中的一只鸟（粒子），所有的粒子都有一个由被优化的函数决定的适应值，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

所有的粒子具有以下两个属性：速度、位置，其迭代公式为：

速度更新公式：

为第k+1时刻，第i个粒子的速度，为惯性权重， C1和C2分别为局部搜索和全局搜索的能力常量。

位置更新公式：

为第i个粒子k时刻的位置，分别为当前最优解和全局最优解。

a和b为0~1之间的随机值。

适应度公式：
适应度函数跟想要实现什么功能有关，把粒子对应成你问题的候选解，适应度函数用来评价给出的这个候选解（粒子）的好坏（好坏的评价标准需要一个量化指标，也就是，粒子的适应度值）。比如你想求出N维空间中离原点最近的点（答案当然是原点，现在假设不知道答案） 设定粒子维数为N，表示候选解。 那适应度函数值可以表示为 f = x1^2 + x2^2 +..................xN^2 只要选择适应度函数值最小的那组解救可以了。

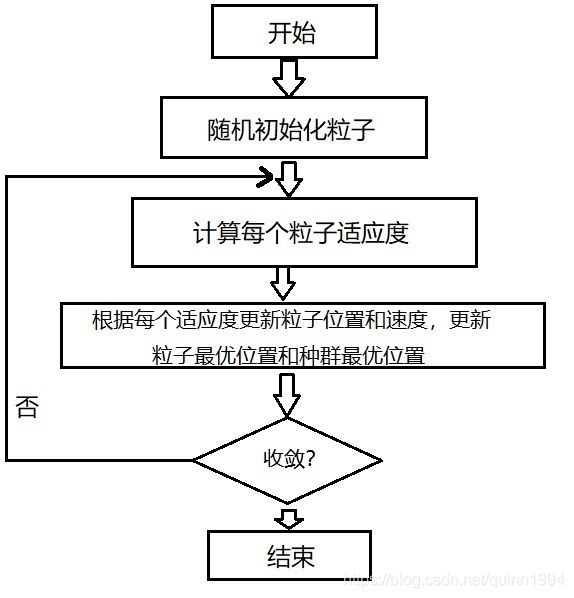
算法流程图如下：

 

PSO.py

import numpy as np
import random


def fit_fun(X):  # 适应函数
    return -np.abs(np.sin(X[0]) * np.cos(X[1]) * np.exp(np.abs(1 - np.sqrt(X[0] ** 2 + X[1] ** 2) / np.pi)))
   #构建适应度函数，求解函数为Holder函数：sin(x)*cos(y)*e(|1-sqrt(x**2+y**2)/2|)

class Particle:
    # 初始化
    def __init__(self, x_max, max_vel, dim):
        self.__pos = [random.uniform(-x_max, x_max) for i in range(dim)]  # 粒子在i维空间的位置
        # 粒子的位置，随机赋予在区间（-x_max, x_max）初值
        self.__vel = [random.uniform(-max_vel, max_vel) for i in range(dim)]  # 粒子在i维空间的速度
        # 粒子的速度，随机赋予在区间（-x_max, x_max）初值
        self.__bestPos = [0.0 for i in range(dim)]  
        # 粒子在i个维度上最好的位置，将每个方向的粒子都赋予0.0
        self.__fitnessValue = fit_fun(self.__pos)  # 适应度函数值

    def set_pos(self, i, value):
        self.__pos[i] = value #位置/解

    def get_pos(self):    #返回位置/解
        return self.__pos

    def set_best_pos(self, i, value):#粒子最优位置/解
        self.__bestPos[i] = value  

    def get_best_pos(self):
        return self.__bestPos#返回粒子位置/解

    def set_vel(self, i, value):#速度
        self.__vel[i] = value 

    def get_vel(self):
        return self.__vel#返回速度

    def set_fitness_value(self, value):
        self.__fitnessValue = value   #粒子适应度

    def get_fitness_value(self):
        return self.__fitnessValue   #返回粒子适应度


class PSO:
    def __init__(self, dim, size, iter_num, x_max, max_vel, best_fitness_value=float('Inf'), C1=2, C2=2, W=1, Gamma=1.4):
        self.C1 = C1
        self.C2 = C2
        self.Gamma= Gamma #调整迭代的速度
        self.W = W        #惯性权重
        self.dim = dim  # 粒子的维度
        self.size = size  # 粒子个数
        self.iter_num = iter_num  # 迭代次数
        self.x_max = x_max     #最大解/位置
        self.max_vel = max_vel  # 粒子最大速度
        self.best_fitness_value = best_fitness_value
        self.best_position = [0.0 for i in range(dim)]  # 种群最优位置
        self.fitness_val_list = []  # 每次迭代最优适应值

        # 对粒子群所有粒子参数进行初始化
        self.Particle_list = [Particle(self.x_max, self.max_vel, self.dim) for i in range(self.size)]

    def set_bestFitnessValue(self, value):
        self.best_fitness_value = value

    def get_bestFitnessValue(self):
        return self.best_fitness_value
    # 返回粒子群最优适应度，即本代最优粒子适应度


    def set_bestPosition(self, i, value):
        self.best_position[i] = value
      # 更新本代粒子群最优位置，令本代最优粒子的位置/解为本代粒子群最优位置


    def get_bestPosition(self):
        return self.best_position
    # 返回粒子群最优位置，即本代最优粒子的位置/解


    # 更新粒子速度
    def update_vel(self, part):
        for i in range(self.dim):#更新粒子第i维的速度
            vel_value = self.W * part.get_vel()[i] + self.C1 * random.random() * (part.get_best_pos()[i] - part.get_pos()[i]) \
                        + self.C2 * random.random() * (self.get_bestPosition()[i] - part.get_pos()[i])
            #权重*上代粒子第i维度的速度+c1*random*(粒子上代在i维度的最优位置-粒子当前在第i维度的最位置)
            #   +c2*random*(上代粒子群在i维的最优位置-粒子当前在第i维度的最位置)
            if vel_value > self.max_vel:
                vel_value = self.max_vel   #限速
            elif vel_value < -self.max_vel:
                vel_value = -self.max_vel
            part.set_vel(i, vel_value)  #在各个维度更新位置

    # 更新粒子的位置
    def update_pos(self, part):
        for i in range(self.dim):   #更新粒子第i维度的位置
            pos_value = part.get_pos()[i] + self.Gamma*part.get_vel()[i]
            part.set_pos(i, pos_value)#位置更新公式
        value = fit_fun(part.get_pos())#更新粒子解的适应度
        if value < part.get_fitness_value():#如果粒子的适应度小于上代粒子适应度
            part.set_fitness_value(value) #则保留
            for i in range(self.dim):    
                part.set_best_pos(i, part.get_pos()[i])#将i维中的最优位置作为粒子的最优位置
            #如果粒子的适应度大于上代粒子适应度则抛弃


        if value < self.get_bestFitnessValue():
            #如果粒子的适应度优于于粒子群全局适应度，则保留
            self.set_bestFitnessValue(value)
            for i in range(self.dim):
                self.set_bestPosition(i, part.get_pos()[i])#更新粒子群最优位置
         
    def update(self):    #更新粒子群
        for i in range(self.iter_num):
            for part in self.Particle_list:
                self.update_vel(part)  # 更新速度
                self.update_pos(part)  # 更新位置
            self.fitness_val_list.append(self.get_bestFitnessValue())  # 每次迭代完把当前的最优适应度存到列表/即，把最优函数极值保存
        return self.fitness_val_list, self.get_bestPosition()

test.py

 

import PSO
import matplotlib.pyplot as plt
import numpy as np


dim = 2
size = 20
iter_num = 1000
x_max = 10
max_vel = 0.5

pso = PSO.PSO(dim, size, iter_num, x_max, max_vel,)  #初始化
fit_var_list, best_pos = pso.update()   #执行PSO
print("最优解:" + str(best_pos))  
print("最优值:" + str(fit_var_list[-1])) 
plt.plot(np.linspace(0, iter_num, iter_num), fit_var_list, c="r", alpha=0.5)
plt.show()

程序中，我们采用维度这一概念。维度的本质其实就是模拟粒子的方向，即对当前粒子的多个方向进行多次计算。以多次重复计算方法实现对多个方向寻解的方法。

经过测试发现，比较容易陷入局部最优解：

f(8.0976253838002, 6.480369504941845)=-9.504673324949687;

f(-8.1004040728734, -6.47981022046396)=-9.504636698476002

f(8.09545161260645, -6.48036019465368)=-9.504651029513745

f(-8.09993902133437, 6.47538746374264)=-9.504568797304843

f(-1.62251583841027, -9.7292577958573)=-8.095120892624823

f(1.620608971827874, -9.7290992535129)=-8.095120892624823

等~~~