动态规划之最优二叉搜索树
我们在之前也讨论过动态规划的例子:
动态规划原理:http://blog.csdn.net/ii1245712564/article/details/45040037
钢条切割问题:http://blog.csdn.net/ii1245712564/article/details/44464689
矩阵链乘法问题:http://blog.csdn.net/ii1245712564/article/details/44464689
最长公共子序列:http://blog.csdn.net/ii1245712564/article/details/45056045
这次我们来讨论另外一个动态规划的例子,最优二叉搜索树。
在进入主题之前,我们先提一下动态规划的两大特征:
- 具有最优子结构
- 子问题重叠
问题背景
假设现在我们要做一个软件,需要将英文按照单词翻译成中文,每一个英文单词都有一个对应的中文解释。现在我们需要将这些英文单词单词进行排序,然后将这些英文单词无差别的加入到二叉搜索树里面!每一个单词都要进行搜索,我们要求所需的时间尽可能的少,我们可以通过红黑树或者其他平衡搜索结构使得每次搜索时间为 log(n) 。
但是这里有个问题,每一个单词出现的频率都不一样。比如the出现的概率就比其他单词出现的概率大得多,要是我们将the放在搜索树的叶子上,那么每次都要从搜索树的根一直搜查到叶子,那将是很费时间的。那么我们要尽量将概率大的单词放在靠近根部的位置,概率小的单词放在靠近叶子的位置。
问题描述
给定一个n个不同关键字已排序的序列 K=<k1,k2,k3,...kn>(k1<k2<k3<...<kn) .我们希望用这些不同的关键字构建一棵二叉搜索树。其中每一个 ki 都有一个对应的搜索概率 pi ,有些要搜索的值不在 K 中,于是我们还有 n+1 个伪关键字, D=<d0,d1,d2,...,dn> ,其中 di 表示比 ki−1 大且比 ki 小的伪关键字,对应的每一个伪关键字 di ,也有一个相应的搜索概率 qi ,这里的 di 也可以理解为在找不到关键字的情况。
于是我们得出:
假设我们有这样的关键字和伪关键字序列:
构建出下面两棵搜索树:
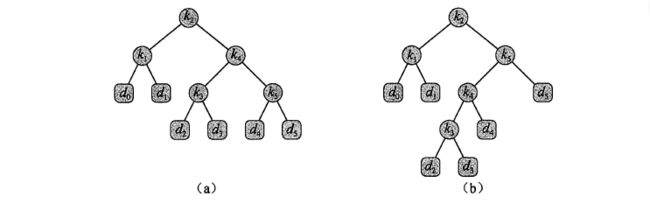
我们求一棵二叉搜索树的权重为:
用上面的公式,我们计算得
a 树的搜索代价为: E[Ta]=2.80
b 树的搜索代价为 : E[Tb]=2.75
对于一个给定的概率集合,我们希望构造出一棵搜索代价最小的二叉搜索树,那么构造出来的二叉搜索树就是最优二叉搜索树!
问题分析
我们先来尝试一下蛮力法:对于一个序列,每一个关键字都有成为根节点的可能性,于是在排除伪关键字的情况下问题的规模为 2∗2∗2∗...∗2=2n ,要是再加上伪关键字,那么问题的规模就更大了,所以这里问题的规模使我们最不想要的指数级的,那么来世老规矩,动态规划出场!没有动态规划还真不行啊
最优二叉搜索树的结构
我们在《动态规划原理》里面提到过,需找一个问题的最优子结构的步骤:
- 选择:我们在构建最优二叉搜索树的过程中,我们首先选出一个节点 kr .
- 假设:假设节点 kr 是最优二叉搜索树根节点.
- 子问题:这里我们就产生了两个子问题: K1<k1,...,kr−1> 和 K2<kr+1,...,n>
- 剪切粘贴:这里的子问题 K1 和 K2 也是最优二叉搜索树,假设 K1 不是最优二叉搜索树,那么我们将 K1 当前的搜索树剪掉,将 K1 的最优二叉搜索树粘贴进去,得到一棵更优的二叉搜索树,这与原问题矛盾,不成立!所以这里最优二叉搜索树具有最优子结构!
一个递归算法
我们首先假设问题的域为ki ki 到kj kj ,其中i>=1, j <=n且j>=n-1 i>=1,j<=n且j>=n−1 , e[i...j] 表示 i到j 的最小搜索代价!
于是我们有:
- 当 i=j−1 时,这时没有任何的关键字在二叉搜索树中,只包含了为关键字 di−1 ,即 e[i,i−1]=qi−1
- 当 i>j−1 时,我们需要在 i 到 j−1 之前选择一个节点 r ,使得搜索代价最小.即:
e[i,j]=pr+(e[i,r−1]+weight(i,r−1))+(e[r+1,j]+weight(r+1,j)).
因为:
pr+weight(i,r−1)+weight(r+1,j)=weight(i,j)
所以上式可以简化为:
e[i,j]=e[i,r−1]+e[r+1,j]+weight(i,j)
上面的第二种情况假定最优点是在r上面,如果选择代价最低者作为根节点,最终得到下面的递归式:
e[i,j]=⎧⎩⎨⎪⎪di−1,min { e[i,i−1]+e[i+1,j]+weight(i,j),e[i,i]+e[i+2,j]+weight(i,j),...,e[i,j]+e[j+1][j]+weight(i,j) } ,i=j−1i<=j
计算最优二叉树的期望搜索代价
下面采用自上而下和自下而上的代码实现:
/*************************************************
* @Filename: searchBinaryTree_v1.cc
* @Author: qeesung
* @Email: [email protected]
* @DateTime: 2015-04-19 09:48:21
* @Version: 1.0
* @Description: 最优二叉搜索树的算法实现,这里首先采用自上而下的求解方法
**************************************************/
#include string , double> > keyMap,\
std::vectorstring , double> > fKeyMap);
/**
* 保存i到j的最优解开
* 为了就算e[i][i-1] e[j+1][j]这种情况,所以将行设了比列多大一维
*/
double minWeightArray[MAX_KEY_COUNT+2][MAX_KEY_COUNT+1];
/**
* 为了保存weight i到j的权重之和,不用每次都计算
* 为了计算weigh[i][i-1]情况,行比列多了一维
*/
double weight[MAX_KEY_COUNT+2][MAX_KEY_COUNT+1];
/**
* 为了递归计算出weight[i][j]的值
* @param i 左边界,需要从1开始
* @param j 右边界
* @param keyMap 关键字序列
* @param fKeyMap 伪关键字序列
* @return i到j的权重
*/
double computeWeight(int i , int j , \
std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
if(i-1 == j)
weight[i][j] = fKeyMap[j].second;
else
weight[i][j]=computeWeight(i , j-1 , keyMap , fKeyMap)+keyMap[j].second+fKeyMap[j].second;
return weight[i][j];
}
/**
* 最优二叉搜索树的接口
* @param keyMap 关键字序列
* @param fKeyMap 伪关键字序列
* @return 返回最优二叉搜索树的权重
*/
double bestBSTree(std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
if(keyMap.size()-1 > MAX_KEY_COUNT)
{
cerr<<"key count should less than "<return 0.0;
}
/** 多次初始化i到j的权重 */
for (int k = 1 ; k <= keyMap.size()-1+1 ; ++k)
{
computeWeight(k , keyMap.size()-1 , keyMap , fKeyMap);
}
cout<<"weight array"<for (int i =1 ; i<= keyMap.size() ; ++i)
{
for (int j = 0 ; jcout<"\t";
}
cout<// 现在已经将权重数据全都保存到weight里面了
//
// 开始计算最优
dealBestBSTree(1,keyMap.size()-1,keyMap , fKeyMap);
cout<<"min weight array"<for (int i =1 ; i<= keyMap.size() ; ++i)
{
for (int j = 0 ; jcout<"\t";
}
cout<return minWeightArray[1][keyMap.size()-1];
}
/**
* 最优二叉搜索树的实际递归函数
* @param i 左边界
* @param j 右边界
* @param keyMap 关键字序列
* @param fKeyMap 伪关键字序列
* @return i到j的最优值
*/
double dealBestBSTree(int i , int j ,\
std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
if(i-1 == j)
{
minWeightArray[i][j] = weight[i][j];
return weight[i][j];
}
if(minWeightArray[i][j]!=0)
return minWeightArray[i][j];
// 表示没有被计算过,现在开始计算
double min= 10.0;
for(int k = i ; k <= j ; ++k)
{
double temp = dealBestBSTree(i , k-1 , keyMap , fKeyMap)+\
dealBestBSTree(k+1,j , keyMap , fKeyMap)+weight[i][j];
if(temp < min)
min = temp;
}
minWeightArray[i][j] = min;
return min;
}
int main(int argc, char const *argv[])
{
std::vectorstring , double> > keyMap;
std::vectorstring , double> > fKeyMap;
// keyMap[0]是用不到的,只是为了填充,因为关键字是从1开始的
keyMap.push_back(pair<string , double>("k1", 0.15));
keyMap.push_back(pair<string , double>("k1", 0.15));
keyMap.push_back(pair<string , double>("k2", 0.1));
keyMap.push_back(pair<string , double>("k3", 0.05));
keyMap.push_back(pair<string , double>("k4", 0.1));
keyMap.push_back(pair<string , double>("k5", 0.2));
fKeyMap.push_back(pair<string , double>("d0", 0.05));
fKeyMap.push_back(pair<string , double>("d1", 0.1));
fKeyMap.push_back(pair<string , double>("d2", 0.05));
fKeyMap.push_back(pair<string , double>("d3", 0.05));
fKeyMap.push_back(pair<string , double>("d4", 0.05));
fKeyMap.push_back(pair<string , double>("d5", 0.1));
cout<<"The binary search tree min weight is:"<while(1);
return 0;
}
/*************************************************
* @Filename: searchBinaryTree_v1.cc
* @Author: qeesung
* @Email: [email protected]
* @DateTime: 2015-04-19 09:48:21
* @Version: 1.0
* @Description: 最优二叉搜索树的算法实现,这里首先采用自下而上的方法求解
**************************************************/
#include string , double> > keyMap,\
std::vectorstring , double> > fKeyMap);
/**
* 保存i到j的最优解开
* 为了就算e[i][i-1] e[j+1][j]这种情况,所以将行设了比列多大一维
*/
double minWeightArray[MAX_KEY_COUNT+2][MAX_KEY_COUNT+1];
/**
* 为了保存weight i到j的权重之和,不用每次都计算
* 为了计算weigh[i][i-1]情况,行比列多了一维
*/
double weight[MAX_KEY_COUNT+2][MAX_KEY_COUNT+1];
/**
* 为了递归计算出weight[i][j]的值
* @param i 左边界,需要从1开始
* @param j 右边界
* @param keyMap 关键字序列
* @param fKeyMap 伪关键字序列
* @return i到j的权重
*/
double computeWeight(int i , int j , \
std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
if(i-1 == j)
weight[i][j] = fKeyMap[j].second;
else
weight[i][j]=computeWeight(i , j-1 , keyMap , fKeyMap)+keyMap[j].second+fKeyMap[j].second;
return weight[i][j];
}
/**
* 最优二叉搜索树的接口
* @param keyMap 关键字序列
* @param fKeyMap 伪关键字序列
* @return 返回最优二叉搜索树的权重
*/
double bestBSTree(std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
if(keyMap.size()-1 > MAX_KEY_COUNT)
{
cerr<<"key count should less than "<return 0.0;
}
/** 多次初始化i到j的权重 */
for (int k = 1 ; k <= keyMap.size()-1+1 ; ++k)
{
computeWeight(k , keyMap.size()-1 , keyMap , fKeyMap);
}
cout<<"weight array"<for (int i =1 ; i<= keyMap.size() ; ++i)
{
for (int j = 0 ; jcout<"\t";
}
cout<// 现在已经将权重数据全都保存到weight里面了
//
// 开始计算最优
dealBestBSTree(1,keyMap.size()-1,keyMap , fKeyMap);
cout<<"min weight array"<for (int i =1 ; i<= keyMap.size() ; ++i)
{
for (int j = 0 ; jcout<"\t";
}
cout<return minWeightArray[1][keyMap.size()-1];
}
/**
* 最优二叉搜索树的实际递归函数
* @param i 左边界
* @param j 右边界
* @param keyMap 关键字序列
* @param fKeyMap 伪关键字序列
* @return i到j的最优值
*/
void dealBestBSTree(int i , int j ,\
std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
// 初始化minWeightArray数组,将 i-1 == j的情况全都赋值
for(int k = i ; k <= j+1 ; ++k)
{
minWeightArray[k][k-1] = weight[k][k-1];
}
// 下面自下而上的来求解
for(int k = 0 ; k < j-i+1 ; ++k)
{
for(int m = i ; m <= j ; ++m)
{
double min = 10.0;
for(int w = m ; w <= m+k ; ++w )
{
double temp = minWeightArray[m][w-1]+minWeightArray[w+1][m+k]+weight[m][m+k];
if(temp < min)
min = temp;
}
minWeightArray[m][m+k] = min;
}
}
}
int main(int argc, char const *argv[])
{
std::vectorstring , double> > keyMap;
std::vectorstring , double> > fKeyMap;
// keyMap[0]是用不到的,只是为了填充,因为关键字是从1开始的
keyMap.push_back(pair<string , double>("k1", 0.15));
keyMap.push_back(pair<string , double>("k1", 0.15));
keyMap.push_back(pair<string , double>("k2", 0.1));
keyMap.push_back(pair<string , double>("k3", 0.05));
keyMap.push_back(pair<string , double>("k4", 0.1));
keyMap.push_back(pair<string , double>("k5", 0.2));
fKeyMap.push_back(pair<string , double>("d0", 0.05));
fKeyMap.push_back(pair<string , double>("d1", 0.1));
fKeyMap.push_back(pair<string , double>("d2", 0.05));
fKeyMap.push_back(pair<string , double>("d3", 0.05));
fKeyMap.push_back(pair<string , double>("d4", 0.05));
fKeyMap.push_back(pair<string , double>("d5", 0.1));
cout<<"The binary search tree min weight is:"<while(1);
return 0;
}
下面两个是带有求解决方案的代码,也是自上而下和自下而上的:
/*************************************************
* @Filename: searchBinaryTree_v1.cc
* @Author: qeesung
* @Email: [email protected]
* @DateTime: 2015-04-19 09:48:21
* @Version: 1.0
* @Description: 最优二叉搜索树的算法实现,这里首先采用自上而下的求解方法,这里需要求出最优解
**************************************************/
#include string , double> > keyMap,\
std::vectorstring , double> > fKeyMap);
/**
* 保存i到j的最优解开
* 为了就算e[i][i-1] e[j+1][j]这种情况,所以将行设了比列多大一维
*/
double minWeightArray[MAX_KEY_COUNT+2][MAX_KEY_COUNT+1];
/**
* 为了保存weight i到j的权重之和,不用每次都计算
* 为了计算weigh[i][i-1]情况,行比列多了一维
*/
double weight[MAX_KEY_COUNT+2][MAX_KEY_COUNT+1];
/**
* 保存在i到j的切分点
*/
double rootPoint[MAX_KEY_COUNT][MAX_KEY_COUNT];
void printSolution(int i , int j , std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
if( i == j)
{
cout<<"from "<" to "<" root is "<return;
}
cout<<"from "<" to "<" root is "<1 , keyMap , fKeyMap);
printSolution(rootPoint[i][j]+1 , j , keyMap , fKeyMap);
return;
}
/**
* 为了递归计算出weight[i][j]的值
* @param i 左边界,需要从1开始
* @param j 右边界
* @param keyMap 关键字序列
* @param fKeyMap 伪关键字序列
* @return i到j的权重
*/
double computeWeight(int i , int j , \
std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
if(i-1 == j)
weight[i][j] = fKeyMap[j].second;
else
weight[i][j]=computeWeight(i , j-1 , keyMap , fKeyMap)+keyMap[j].second+fKeyMap[j].second;
return weight[i][j];
}
/**
* 最优二叉搜索树的接口
* @param keyMap 关键字序列
* @param fKeyMap 伪关键字序列
* @return 返回最优二叉搜索树的权重
*/
double bestBSTree(std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
if(keyMap.size()-1 > MAX_KEY_COUNT)
{
cerr<<"key count should less than "<return 0.0;
}
/** 多次初始化i到j的权重 */
for (int k = 1 ; k <= keyMap.size()-1+1 ; ++k)
{
computeWeight(k , keyMap.size()-1 , keyMap , fKeyMap);
}
cout<<"weight array"<for (int i =1 ; i<= keyMap.size() ; ++i)
{
for (int j = 0 ; jcout<"\t";
}
cout<// 现在已经将权重数据全都保存到weight里面了
//
// 开始计算最优
dealBestBSTree(1,keyMap.size()-1,keyMap , fKeyMap);
cout<<"min weight array"<for (int i =1 ; i<= keyMap.size() ; ++i)
{
for (int j = 0 ; jcout<"\t";
}
cout<return minWeightArray[1][keyMap.size()-1];
}
/**
* 最优二叉搜索树的实际递归函数
* @param i 左边界
* @param j 右边界
* @param keyMap 关键字序列
* @param fKeyMap 伪关键字序列
* @return i到j的最优值
*/
double dealBestBSTree(int i , int j ,\
std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
if(i-1 == j)
{
minWeightArray[i][j] = weight[i][j];
return weight[i][j];
}
if(minWeightArray[i][j]!=0)
return minWeightArray[i][j];
// 表示没有被计算过,现在开始计算
double min = 10.0;
int rootPos = i;
for(int k = i ; k <= j ; ++k)
{
double temp = dealBestBSTree(i , k-1 , keyMap , fKeyMap)+\
dealBestBSTree(k+1,j , keyMap , fKeyMap)+weight[i][j];
if(temp < min)
{
min = temp;
rootPos = k;
}
}
minWeightArray[i][j] = min;
rootPoint[i][j] = rootPos;
return min;
}
int main(int argc, char const *argv[])
{
std::vectorstring , double> > keyMap;
std::vectorstring , double> > fKeyMap;
// keyMap[0]是用不到的,只是为了填充,因为关键字是从1开始的
keyMap.push_back(pair<string , double>("k1", 0.15));
keyMap.push_back(pair<string , double>("k1", 0.15));
keyMap.push_back(pair<string , double>("k2", 0.1));
keyMap.push_back(pair<string , double>("k3", 0.05));
keyMap.push_back(pair<string , double>("k4", 0.1));
keyMap.push_back(pair<string , double>("k5", 0.2));
fKeyMap.push_back(pair<string , double>("d0", 0.05));
fKeyMap.push_back(pair<string , double>("d1", 0.1));
fKeyMap.push_back(pair<string , double>("d2", 0.05));
fKeyMap.push_back(pair<string , double>("d3", 0.05));
fKeyMap.push_back(pair<string , double>("d4", 0.05));
fKeyMap.push_back(pair<string , double>("d5", 0.1));
cout<<"The binary search tree min weight is:"<1,keyMap.size()-1,keyMap , fKeyMap);
while(1);
return 0;
}
/*************************************************
* @Filename: searchBinaryTree_v1.cc
* @Author: qeesung
* @Email: [email protected]
* @DateTime: 2015-04-19 09:48:21
* @Version: 1.0
* @Description: 最优二叉搜索树的算法实现,这里首先采用自下而上的方法求解,带有解决方案
**************************************************/
#include string , double> > keyMap,\
std::vectorstring , double> > fKeyMap);
/**
* 保存i到j的最优解开
* 为了就算e[i][i-1] e[j+1][j]这种情况,所以将行设了比列多大一维
*/
double minWeightArray[MAX_KEY_COUNT+2][MAX_KEY_COUNT+1];
/**
* 为了保存weight i到j的权重之和,不用每次都计算
* 为了计算weigh[i][i-1]情况,行比列多了一维
*/
double weight[MAX_KEY_COUNT+2][MAX_KEY_COUNT+1];
/**
* 保存在i到j的切分点
*/
double rootPoint[MAX_KEY_COUNT][MAX_KEY_COUNT];
void printSolution(int i , int j , std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
if( i == j)
{
cout<<"from "<" to "<" root is "<return;
}
cout<<"from "<" to "<" root is "<1 , keyMap , fKeyMap);
printSolution(rootPoint[i][j]+1 , j , keyMap , fKeyMap);
return;
}
/**
* 为了递归计算出weight[i][j]的值
* @param i 左边界,需要从1开始
* @param j 右边界
* @param keyMap 关键字序列
* @param fKeyMap 伪关键字序列
* @return i到j的权重
*/
double computeWeight(int i , int j , \
std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
if(i-1 == j)
weight[i][j] = fKeyMap[j].second;
else
weight[i][j]=computeWeight(i , j-1 , keyMap , fKeyMap)+keyMap[j].second+fKeyMap[j].second;
return weight[i][j];
}
/**
* 最优二叉搜索树的接口
* @param keyMap 关键字序列
* @param fKeyMap 伪关键字序列
* @return 返回最优二叉搜索树的权重
*/
double bestBSTree(std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
if(keyMap.size()-1 > MAX_KEY_COUNT)
{
cerr<<"key count should less than "<return 0.0;
}
/** 多次初始化i到j的权重 */
for (int k = 1 ; k <= keyMap.size()-1+1 ; ++k)
{
computeWeight(k , keyMap.size()-1 , keyMap , fKeyMap);
}
cout<<"weight array"<for (int i =1 ; i<= keyMap.size() ; ++i)
{
for (int j = 0 ; jcout<"\t";
}
cout<// 现在已经将权重数据全都保存到weight里面了
//
// 开始计算最优
dealBestBSTree(1,keyMap.size()-1,keyMap , fKeyMap);
cout<<"min weight array"<for (int i =1 ; i<= keyMap.size() ; ++i)
{
for (int j = 0 ; jcout<"\t";
}
cout<return minWeightArray[1][keyMap.size()-1];
}
/**
* 最优二叉搜索树的实际递归函数
* @param i 左边界
* @param j 右边界
* @param keyMap 关键字序列
* @param fKeyMap 伪关键字序列
* @return i到j的最优值
*/
void dealBestBSTree(int i , int j ,\
std::vectorstring , double> > keyMap,\
std::vectorstring , double> > fKeyMap)
{
// 初始化minWeightArray数组,将 i-1 == j的情况全都赋值
for(int k = i ; k <= j+1 ; ++k)
{
minWeightArray[k][k-1] = weight[k][k-1];
}
// 下面自下而上的来求解
for(int k = 0 ; k < j-i+1 ; ++k)
{
for(int m = i ; m <= j ; ++m)
{
double min = 10.0;
int rootPos = i;
for(int w = m ; w <= m+k ; ++w )
{
double temp = minWeightArray[m][w-1]+minWeightArray[w+1][m+k]+weight[m][m+k];
if(temp < min)
{
min = temp;
rootPos = w;
}
}
rootPoint[m][m+k] = rootPos;
minWeightArray[m][m+k] = min;
}
}
}
int main(int argc, char const *argv[])
{
std::vectorstring , double> > keyMap;
std::vectorstring , double> > fKeyMap;
// keyMap[0]是用不到的,只是为了填充,因为关键字是从1开始的
keyMap.push_back(pair<string , double>("k1", 0.15));
keyMap.push_back(pair<string , double>("k1", 0.15));
keyMap.push_back(pair<string , double>("k2", 0.1));
keyMap.push_back(pair<string , double>("k3", 0.05));
keyMap.push_back(pair<string , double>("k4", 0.1));
keyMap.push_back(pair<string , double>("k5", 0.2));
fKeyMap.push_back(pair<string , double>("d0", 0.05));
fKeyMap.push_back(pair<string , double>("d1", 0.1));
fKeyMap.push_back(pair<string , double>("d2", 0.05));
fKeyMap.push_back(pair<string , double>("d3", 0.05));
fKeyMap.push_back(pair<string , double>("d4", 0.05));
fKeyMap.push_back(pair<string , double>("d5", 0.1));
cout<<"The binary search tree min weight is:"<1,keyMap.size()-1,keyMap , fKeyMap);
while(1);
return 0;
}