python numpy 傅里叶变换与频域图

python numpy 傅里叶变换与频域图

"""
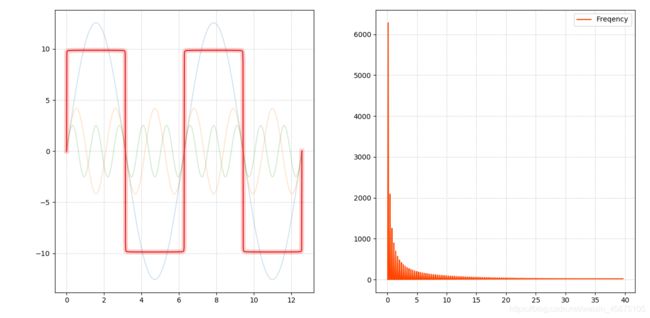
    三角函数 合成方波
    傅里叶变换与逆傅里叶变换
	绘制频域图
"""
import numpy as np
import matplotlib.pyplot as mp
import numpy.fft as nf

# 准备x值与y值
x = np.linspace(0, np.pi * 4, 1000)
y1 = 4 * np.pi * np.sin(x)
y2 = 4 / 3 * np.pi * np.sin(3 * x)
y3 = 4 / 5 * np.pi * np.sin(5 * x)

# 叠加1000条曲线 组成方波
n = 1000
y = np.zeros(n)
for i in range(1, n + 1):
    y += 4 / (2 * i - 1) * np.pi * np.sin((2 * i - 1) * x)

# 绘制方波图片
mp.subplot(121)
mp.grid(linestyle=":")
mp.plot(x, y1, label="y1", alpha=0.2)
mp.plot(x, y2, label="y2", alpha=0.2)
mp.plot(x, y3, label="y3", alpha=0.2)
mp.plot(x, y, label="y")

# 傅里叶变换 对Y执行
# 结果是复数
complex_ary = nf.fft(y)
print(complex_ary.shape, complex_ary.dtype)

# 逆傅里叶变换
y_ = nf.ifft(complex_ary).real

# 绘制逆傅里叶变换值
mp.plot(x, y_, label="y_", color="red", linewidth=7, alpha=0.2)
mp.tight_layout()

# 绘制频域图像
# 计算频域 参数：采样数量  采样周期  X 轴
fft_freq = nf.fftfreq(y_.size, x[1] - x[0])
fft_pow = np.abs(complex_ary)  # 复数的摸-->能量  Y轴

mp.subplot(122)
mp.grid(linestyle=":")
mp.plot(fft_freq[fft_freq > 0], fft_pow[fft_freq > 0], color="orangered", label="Freqency")
mp.legend()
mp.tight_layout()

mp.show()