凉脾的题解

D - Keeping On Track

Acmar and Ibmar are at war! You are in charge of a rail network that transports important supplies throughout the great state of Acmar during this delicate time. The rail system is made up of a set of rail lines which meet at various junction points. While there is no limit to the number of rail lines that can meet at a junction, the network is set up so that there is only one path between any two junctions. You’ve tried to argue for some redundancy in the system, i.e., extra rail lines so that there are two or more paths connecting some junctions, but it’s wartime and budgets are tight.

However, this may soon change as you’ve just been given some terrible news from double agents working in Ibmar: within the next month enemy spies plan to blow up one of the junctions! Unfortunately, the exact junction is not known, but knowing your enemy well you are certain that they will undoubtedly strike the critical junction, specifically the junction whose removal disconnects the most pairs of other remaining junctions in the system. You don’t have much time to act, so the most you can do is add one new line connecting two currently unconnected junctions, thereby reducing the number of disconnected pairs after the critical junction has been destroyed. Your job is to determine how to make the number of disconnected pairs as small as possible by adding in the best possible rail line.

Input

Input starts with a line containing an integer n (2≤n≤10000) indicating the number of rail lines in the system. Following that are n lines of the form i1 i2 indicating that a rail line connects junctions i1 and i2. Junctions are numbered consecutively starting at 0. All rail lines are two-way and no rail line appears more than once in the input. There is exactly one path between any two junction points given in the input.

Output

Display two values n1 and n2, where n1 is the number of pairs of junctions which will be disconnected when the enemy destroys the critical junction, and n2 is the number of pairs of junctions still disconnected after you add in the best possible rail line. There will never be more than one critical junction.

Sample Input 1
6
0 1
1 2
2 3
2 4
4 5
4 6
Sample Output 1
11 5
Sample Input 2
2
2 1
0 1
Sample Output 2
1 0

题解

假设一个图里有两个联通块,那么不连接的点对数便是这两个联通块内节点个数的乘积
那么,对于一颗树,我们删去其中一个节点
结果为,原树剩余节点$\times$它的每个子树的节点
如下图

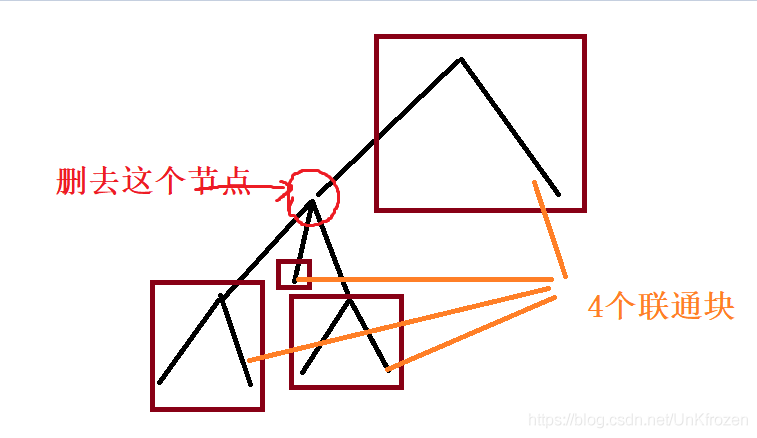
那么,对于每个节点,我们只要分别求得相应联通块的节点数即可
显然,统计一个点的子树大小,只需要dfs进行回溯即可

#pragma comment(linker, "/STACK:102400000,102400000")
#include 
#include 
using namespace std;
using namespace __gnu_pbds;
const double pi = acos(-1.0);
const double eps = 1e-12;
const int MAXN = 1e5 + 10;
const int inf = __LONG_MAX__;
const int enf = LONG_MIN;
const long long INF = LLONG_MAX;
const long long ENF = LLONG_MIN;

vector<int> e[MAXN];
int sum[MAXN], n, ans, cnt;
void dfs(int cur, int fa)
{
     
    sum[cur] = 1;
    vector<int> v;
    for (auto it : e[cur]) {
     
        if (it == fa)
            continue;
        dfs(it, cur);
        sum[cur] += sum[it];
        v.push_back(sum[it]);
    }
    if (v.empty())
        return;
    v.push_back(n - sum[cur]);
    sort(v.begin(), v.end());
    int tmp = 0;
    for (auto it : v)
        tmp += it * (n - it - 1);
    if (ans < tmp / 2) //cnt=两个最大联通块乘积
        ans = tmp / 2, cnt = ans - v.back() * v[v.size() - 2];
}
int main()
{
     
    cin >> n;
    for (int i = 1; i <= n; i++) {
     
        int u, v;
        cin >> u >> v;
        e[u].push_back(v);
        e[v].push_back(u);
    }
    n++;    //边数
    dfs(1, -1);
    cout<<ans<<' '<<cnt<<endl;
    return 0;
}

E - A Question of Ingestion

Stan Ford is a typical college graduate student, meaning that one of the most important things on his mind is where his next meal will be. Fortune has smiled on him as he’s been invited to a multi-course barbecue put on by some of the corporate sponsors of his research team, where each course lasts exactly one hour. Stan is a bit of an analytical type and has determined that his eating pattern over a set of consecutive hours is always very consistent. In the first hour, he can eat up to m calories (where m depends on factors such as stress, bio-rhythms, position of the planets, etc.), but that amount goes down by a factor of two-thirds each consecutive hour afterwards (always truncating in cases of fractions of a calorie). However, if he stops eating for one hour, the next hour he can eat at the same rate as he did before he stopped. So, for example, if m=900 and he ate for five consecutive hours, the most he could eat each of those hours would be 900, 600, 400, 266 and 177 calories, respectively. If, however, he didn’t eat in the third hour, he could then eat 900, 600, 0, 600 and 400 calories in each of those hours. Furthermore, if Stan can refrain from eating for two hours, then the hour after that he’s capable of eating m calories again. In the example above, if Stan didn’t eat during the third and fourth hours, then he could consume 900, 600, 0, 0 and 900 calories.

Stan is waiting to hear what will be served each hour of the barbecue as he realizes that the menu will determine when and how often he should refrain from eating. For example, if the barbecue lasts 5 hours and the courses served each hour have calories 800, 700, 400, 300, 200 then the best strategy when m=900 is to eat every hour for a total consumption of 800+600+400+266+177=2243 calories. If however, the third course is reduced from 400 calories to 40 calories (some low-calorie celery dish), then the best strategy is to not eat during the third hour — this results in a total consumption of 1900 calories.

The prospect of all this upcoming food has got Stan so frazzled he can’t think straight. Given the number of courses and the number of calories for each course, can you determine the maximum amount of calories Stan can eat?

Input

Input starts with a line containing two positive integers n m (n≤100,m≤20000) indicating the number of courses and the number of calories Stan can eat in the first hour, respectively. The next line contains n positive integers indicating the number of calories for each course.

Output

Display the maximum number of calories Stan can consume.

Sample Input 1
5 900
800 700 400 300 200
Sample Output 1
2243
Sample Input 2
5 900
800 700 40 300 200
Sample Output 2
1900

题解

详情看注释

#pragma comment(linker, "/STACK:102400000,102400000")
#include 
#include 
using namespace std;
using namespace __gnu_pbds;
const double pi = acos(-1.0);
const double eps = 1e-12;
const int MAXN = 1e3 + 10;
const int inf = __LONG_MAX__;
const int enf = LONG_MIN;
const long long INF = LLONG_MAX;
const long long ENF = LLONG_MIN;

int a[MAXN], dp[MAXN][MAXN], mul[MAXN];

int main()
{
     
    int n, m;
    cin >> n >> m;
    mul[1] = m;
    for (int i = 2; i <= 100; i++)
        mul[i] = mul[i - 1] * 2 / 3;
    memset(dp, -1, sizeof(dp));
    for (int i = 1; i <= n; i++) {
     
        cin >> a[i];
        dp[i][1] = 0;
    }
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) {
     
            if (dp[i][j] < 0)
                continue;
            int tmp = dp[i][j] + min(mul[j], a[i]); //如果今天吃饭,那么今天的值为之前的值加min()
            dp[i + 1][j + 1] = max(dp[i + 1][j + 1], tmp);  //今天吃了,明天也吃,那么明天的饭量要乘j+1,取最值是因为还要求和
            dp[i + 2][j] = max(dp[i + 2][j], tmp);  //后天也吃,那么饭量不变,到了该天的时候,只需要再判断是否吃饭
            dp[i + 3][1] = max(dp[i + 3][1], tmp);  //大后天饭量恢复为最开始的时候
        }
    int ans = 0;
    for (int i = 1; i <= n+1; i++)
        ans = max(ans, dp[n+1][i]);
    cout << ans << endl;
    return 0;
}