Piece of Cake Contest1872 - 2019年我能变强组队训练赛第十七场（UPC）

Piece of Cake

Alice received a cake for her birthday! Her cake can be described by a convex polygon with n vertices. No three vertices are collinear.

Alice will now choose exactly k random vertices (k≥3) from her cake and cut a piece, the shape of which is the convex polygon defined by those vertices. Compute the expected area of this piece of cake.

Input
Each test case will begin with a line with two space-separated integers n and k (3≤k≤n≤2500), where n is the number of vertices of the cake, and k is the number of vertices of the piece that Alice cuts.

Each of the next n lines will contain two space-separated real numbers x and y (−10.0≤x,y≤10.0), where (x,y) is a vertex of the cake. The vertices will be listed in clockwise order. No three vertices will be collinear. All real numbers have at most 6 digits after the decimal point.

Output
Output a single real number, which is the expected area of the piece of cake that Alice cuts out. Your answer will be accepted if it is within an absolute error of 10−6.
Sample Input1

4 3
0 0
1 1
2 1
1 0

Sample Output1
0.5000000

题意：
按照顺时针的顺序，给出n个多边形的顶点，那么问，从这n个点钟取k个点组成的多边形的面积的平均值是多少呢？？

分析：
直接暴力是会时间超限的，那么怎么处理呢？？？

给你一个二维平面的点，而且还是按照一定的顺序给出的，那么肯定会想到是用到向量的叉乘去求得面积（对于向量的叉乘求面积的方法，大家最好可以好好理解一下，要不然这题目的代码思路还是不太好理解的）；
举个栗子：

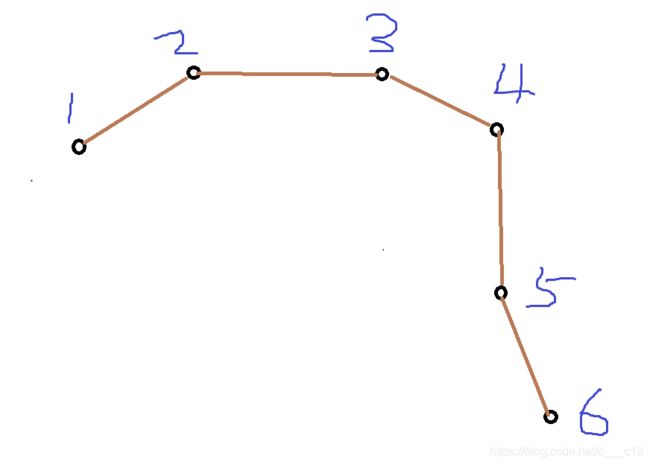
如上图所示，给出5个点，假设k为3，那么由向量的叉乘可知（有一种求面积的方法，是以原点为一个起点求出面积的），由两个点，通过叉乘就可以得出一个三角形的面积，那么假设当前取得的点是2,3，那么剩下的就是从4–6之间选择一个点的情况了，因为k=3嘛；

为啥第三个点不考虑1号点呢，因为1号点与2,3的组合情况在枚举1号点的时候就已经求出了，所以就不用了重复计算了；

由于叉乘是具有方向性，记得要加上反向的情况；
还有这题一定要用long double 否则会wa

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define rep(i,a,b) for(int i=a;i<=b;i++)
typedef long long ll;
using namespace std;
const int N=1e5+10;
const int INF=0x3f3f3f3f;
int n,k;
long double c[2510][2510];
struct node{
     
    long double x,y;
}num[N];
long double area(node a,node b){
     
    return (a.x*b.y-b.x*a.y);
}
void init(){
     
    c[0][0]=1.0;
    for(int i=1;i<=2500;i++){
     
        c[i][0]=1.0;
        for(int j=1;j<i;j++)
            c[i][j]=c[i-1][j]+c[i-1][j-1];
        c[i][i]=1.0;
    }
}
int main()
{
     
//    #ifndef ONLINE_JUDGE
//    freopen("in.txt","r",stdin);
//    #endif // ONLINE_JUDGE
    ios::sync_with_stdio(0);
    init();
    cin>>n>>k;
    for(int i=n;i>=1;i--)
        cin>>num[i].x>>num[i].y;

    long double sum=0.0;

    for(int i=1;i<=n;i++){
     
        for(int j=i+1;j<=n;j++){
     
            sum+=area(num[i],num[j])*c[n-(j-i+1)][k-2];//剩下的点n-(j-i+1)个点中取k-2个组合数，然后乘以当前两个点组成的面积，就是这个情况能组成的所有面积的情况
            sum+=area(num[j],num[i])*c[j-i-1][k-2];//反向
        }
    }
    sum/=2.0;
    cout<< setprecision(8) <<fixed<<sum/c[n][k]<<endl;
    return 0;
}