减治法（三） 生成子集的减治算法及二进制码法

子集问题是指生成一个集合的全部子集（2^n个，包括空集和全集），今年实验室一个去高盛的同学在技术面中被问到了这个问题，另外记得还有一个快排的时间复杂度证明（这个更难，就算了，有时间去看看算法导论怎么证明的）



算法1：减一治策略

有了减治生成排列的经验，相信对于子集来说，用减治法来思考就更加简单了。

如果有了n-1个元素的全部子集项{ 2^(n-1) 项}，那么n个元素的全部子集首先包含这已经有的n-1个元素的全部子集，另外还包括把第n个元素加到每一个子集项里面去生成的子集项{ 也是2^(n-1) 项  }，所以，正好这就有了2^(n-1) + 2^(n-1)  =   2^n项，正是我们要的结果。

为什么说它比排列还简单点呢？因为你只需要把第n个元素加到之前的子集项去就行了，而排列要把它加到一个排列项的不同位置（也就是说原来一个排列项会发展出多个不同的排列项）。

public static String[] getSubSet( char [] aaa){
// 从aaa生成子集，放在String数组返回
int Mi = mi2(aaa.length);
String[] result = new String[Mi];

if (aaa.length == 1 )
{
result[ 0 ] = " 空集 " ;
result[ 1 ] = aaa[ 0 ] + "" ;
}
else // 减一治递归的生成子集
{
int tempMi = mi2(aaa.length - 1 );
String[] tempResult = new String[tempMi];
char [] tempaaa = new char [aaa.length - 1 ];
for ( int i = 0 ;i < aaa.length - 1 ;i ++ )
tempaaa[i] = aaa[i];
tempResult = getSubSet(tempaaa); // 递归产生前n-1项的子集
char an = aaa[aaa.length - 1 ];

// 从前n-1项的子集产生第n项的子集
for ( int i = 0 ;i < tempResult.length;i ++ )
result[i] = tempResult[i];
for ( int i = tempResult.length;i < result.length;i ++ )
{
if (tempResult[i - tempResult.length].equals( " 空集 " ))
result[i] = an + "" ;
else
result[i] = tempResult[i - tempResult.length] + an;
}
}
return result;
}

算法2：二进制的方法来生成子集


减一治的策略虽然已经相当简洁明了，但巧妙的是，却又更加巧合的事情：

一个集合元素对应的自己恰是二进制码从0到最大时的每个二进制串可以表示的：

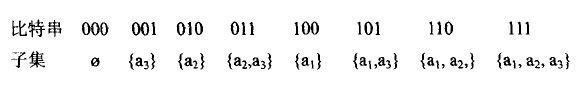
public static String[] binarySubSet( char [] aaa){
// 用二进制的方法产生子集
int Mi = mi2(aaa.length);
String[] result = new String[Mi];
// String binary = "";

for ( int i = 0 ;i < Mi;i ++ )
{
// 将i转换为二进制的一个字符串，串长为aaa.length
String binary = "" ;
int temp = i;
for ( int j = 0 ;j < aaa.length;j ++ )
{
int yushu = temp % 2 ;
temp = temp / 2 ;
binary = yushu + binary;
}

// 每个二进制字符串对应一个子集
result[i] = binaryToString(aaa,binary);
}

return result;
}

完整代码及支持方法：

SubSet

package Section5;

import java.util.Scanner;


/* 第5章 减治法 生成子集 */

public class SubSet {

/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner scan = new Scanner(System.in);
int n = scan.nextInt(); // 输入要生成排列的元素的个数

char [] aaa = new char [n]; // n个要生成子集的元素
String s = scan.next();
for ( int i = 0 ;i < s.length();i ++ )
aaa[i] = s.charAt(i);

System.out.println( " \n减一治递归的构造子集： " );
String[] result1 = getSubSet(aaa); // 结果数组
for ( int i = 0 ;i < result1.length;i ++ )
System.out.print(result1[i] + " " );

System.out.println( " \n\n二进制码方法构造子集： " );
String[] result2 = binarySubSet(aaa);
for ( int i = 0 ;i < result2.length;i ++ )
System.out.print(result2[i] + " " );
}

public static String[] getSubSet( char [] aaa){
// 从aaa生成子集，放在String数组返回
int Mi = mi2(aaa.length);
String[] result = new String[Mi];

if (aaa.length == 1 )
{
result[ 0 ] = " 空集 " ;
result[ 1 ] = aaa[ 0 ] + "" ;
}
else // 减一治递归的生成子集
{
int tempMi = mi2(aaa.length - 1 );
String[] tempResult = new String[tempMi];
char [] tempaaa = new char [aaa.length - 1 ];
for ( int i = 0 ;i < aaa.length - 1 ;i ++ )
tempaaa[i] = aaa[i];
tempResult = getSubSet(tempaaa); // 递归产生前n-1项的子集
char an = aaa[aaa.length - 1 ];

// 从前n-1项的子集产生第n项的子集
for ( int i = 0 ;i < tempResult.length;i ++ )
result[i] = tempResult[i];
for ( int i = tempResult.length;i < result.length;i ++ )
{
if (tempResult[i - tempResult.length].equals( " 空集 " ))
result[i] = an + "" ;
else
result[i] = tempResult[i - tempResult.length] + an;
}
}
return result;
}


public static String[] binarySubSet( char [] aaa){
// 用二进制的方法产生子集
int Mi = mi2(aaa.length);
String[] result = new String[Mi];
// String binary = "";

for ( int i = 0 ;i < Mi;i ++ )
{
// 将i转换为二进制的一个字符串，串长为aaa.length
String binary = "" ;
int temp = i;
for ( int j = 0 ;j < aaa.length;j ++ )
{
int yushu = temp % 2 ;
temp = temp / 2 ;
binary = yushu + binary;
}

// 每个二进制字符串对应一个子集
result[i] = binaryToString(aaa,binary);
}

return result;
}

private static String binaryToString( char [] aaa,String binary){
// 二进制串binary在aaa中对应的字符串
String result = "" ;
for ( int i = 0 ;i < binary.length();i ++ )
if (binary.charAt(i) == ' 1 ' )
result = result + aaa[i];

if (result.equals( "" ))
result = " 空集 " ;

return result;
}

private static int mi2( int n){
// 求n个元素的集合的子集个数--2^n
int result = 1 ;
while (n != 0 )
{
result = result * 2 ;
n -- ;
}
return result;
}
}

运行结果：

4
abcd

减一治递归的构造子集：
空集   a   b   ab   c   ac   bc   abc   d   ad   bd   abd   cd   acd   bcd   abcd  

二进制码方法构造子集：
空集   d   c   cd   b   bd   bc   bcd   a   ad   ac   acd   ab   abd   abc   abcd 


----------------------------------------------------------------------------------------------------------------------------------------------


总结：

思路都比较清晰，但写了好久了，应该再看看具体实现

转载于:https://www.cnblogs.com/jmzz/archive/2011/06/17/2084019.html