算法导论-字符串匹配
编辑文本时,我们经常需要在文本中找到某串模式字符在整个文本中出现的位置,这个模式字符串即为用户查找输入的关键字,解决这个问题的算法为字符串匹配算法。

当我们遇到这个问题,如何查找在文本中出现的模式呢?
一:朴素字符串匹配
我们假设存在两个游标i,j分别指向文本串与模式串的位置,那么有
1:当匹配到T[i]==P[j],则i++,j++;
2:当在匹配到某一位置时出现T[i]!=P[j]时,即匹配失败,此时i回溯到本次开始匹配的位置,j=0
咱们从代码与匹配图解理解朴素算法思路:
int native_string_matcher(char* T,char* P)
{
//获取原始串和模式串字符长度
int n=strlen(T);
int m=strlen(P);
int s=0,i=0;
//原串开始从0至n-m偏移,以匹配模式串
for(s=0;s<=n-m;s++)
{
//模式串从0-m开始分别匹配模式串中字符是否与原串相等
for(i=0;iif(P[i]!=T[s+i]) //如果在匹配过程中有字符不相等,则跳出该循环,偏移S向下移位,继续重新匹配
{
break;
}
if(i==m-1)//当i=m-1,且P最后字符与T最后字符相等,则表示字符串匹配成功,此时返回原串中与模式串相匹配的起始位置。
printf("has match");
return s;
}
}
} OK,现在我们举个栗子,
假设有一个文本字符串和模式字符串如下图

(a) 字符串开始匹配,此时T[0]=P[0],i++为1,此时s+i=1,T[1]!=P[1],匹配失败,s自加1,变为1,开始图(b)的匹配过程;
(b) 此时T[s=1]=c!=P[0],匹配失败,s自加1,变为图c的匹配过程
(c) 此刻T[s=2]=P[0],i自加1,T[s+i=3]=P[i=1],字符相等,继续下一匹配,i自加1为2,T[s+i=4]=P[i=2],且此刻i=length(P),匹配结束。此刻,s继续自加,进行余下字符串的匹配。
朴素字符串匹配过程较简单,但是最坏情况下时间复杂度为O((n-m+1)*m),字符串的匹配时间开销较大,并不能很好的解决字符串的匹配。
补充:
在朴素字符串匹配中存在一种特殊情况,即模式串P中的所有字符都不相同,其匹配时间可以达到O(n),具体的实现代码如下:
int native_string_matcher(char* T,char* P)
{
//获取原始串和模式串字符长度
int n=strlen(T);
int m=strlen(P);
int j=0,i;
for(i=0,j=0;iif(T[i]==P[j]&&jelse{
if(j!=0)
{
j=0;
--i;
}
}
printf("%d\n",i);
if(j==m)
return i-m+1;
}
return -1;//若为-1,代表原始串中不包含模式串
} 这个实现过程很好理解,下面图示匹配过程:
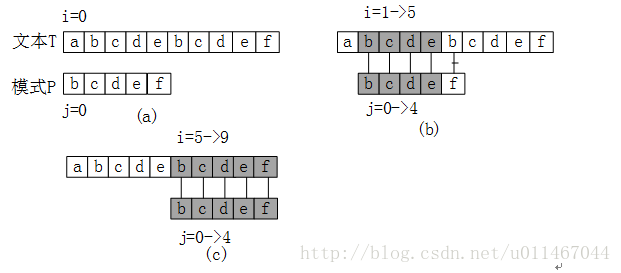
整个匹配流程如下:
(1) 文本串i=0,模式串j=0,此时T[i]!=P[j],匹配失败,i自加1;
(2) 开始匹配,T[1-4]=P[0-3],但T[5]!=P[4],匹配失败,由于P中所有字符互不相同,所以i不必回溯到T[i=2],只需开始匹配T[i-1=4]与P[0]并开始新一轮的匹配过程。
至此,朴素字符串匹配算法结束,整个过程很好理解。
二Rabin-Karp算法
在实际应用中,Rabin-Karp算法的预处理时间为O(m),并且在最坏的情况下的时间复杂度为O((n-m+1)m),相对于朴素字符串,它的运行时是比较好的。整个算法思想介绍如下:
以10进制数来表示字符,例如笔者用0表示a,t同理1表示b,以此类推,那么字符串dbebf可以表示为31415,将字符串看做数字,在算法匹配中更加方便。
给定一个模式串P[1-m],同理在文本串T[s+1..s+m]表示文本串中某段与模式串长度相等的一串字符,那么分别用数字p,t表示这两个字符串,通过比较数字p和t的大小,就可确定字符串是否匹配而无需用模式串中字符依次匹配文本串。示例图如下:

算法的思想理解之后,我们需要思考如何计算p和t.
数学中有霍纳法则,我们运用霍纳法则在O(m)内计算p:
p=P[m]+10(P[m-1]+10(P[m-2]+…+10(P[2]+10P1)…)))
霍纳法则的解释如下:
运用霍纳法则,类似的我们也可以根据T[s+1…s+m]计算出t.
但为了节约时间,我们可以利用一下方法在常数时间内根据ts,计算出ts+1.具体过程如下图解:
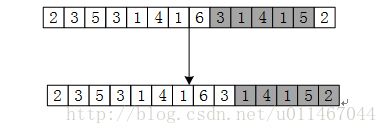
如图所示,ts=31415,ts+1=14152,则
ts+1=(ts-(T[s+1]=3)*10^(m=4))*10+(T[s+m+1]=2)
注:(ts-(T[s+1]=3)*10^(m=4))=31415-30000=1415
即 ts+1=10(ts-10^(m-1)T[s+1])+T[s+m+1]
在计算过程中,可能会出现p与t的值过大,可以取模运算。
下面的代码实现了上述的思想:
#include"stdio.h"
#include"string.h"
#include"math.h"
char* substr(char* p,int start,int end)
{
char *q=malloc(sizeof(char)*(end-start+1));
int i;
for(i=0;i1;i++)
*(q+i)=*(p+start+i);
// *(q+end-start+1)='\0';
return q;
}//取T中T[s+1,s+m]子字符串
void RABIN_KARP_MATCHER(char T[],char P[],int d,int q)
{
int n,m,h,p,t,i,t0=0;
n=strlen(T);
m=strlen(P);
h=((int)pow(d,m-1));
// h=((int)pow(d,m-1))%q;//取模运算
p=0;
t=0;
for(i=0;i<m;i++)
{
p=(d*p+P[i]-'a')%q;//求p
t =(d*t +T[i]-'a')%q;
t0=(d*t0 +T[i]-'a');//求初始t0=num(T[1,m])
}
int s;
for(s=0;s<=n-m;s++)
{
if(p==t&&(strcmp(P,substr(T,s,s+m-1))==0))
// if(p==t)
{
printf("%d\n",s);
}
printf("%d %d %c \n",t,p,T[s]);
int tem=t0;
t0=(d*(tem-(T[s]-'a')*h)+T[s+m]-'a');//求ts+1;
t=t0%q;
// int tem=t;
// t=(d*(tem-(T[s]-'a')*h)+T[s+m]-'a')%q;
}
}
int main()
{
char T[100], P[100];
scanf("%s",T);
scanf("%s",P);
RABIN_KARP_MATCHER(T,P,10,13);
return 0;
} 三:有限自动机
有限自动机:每读入字符串的一个字符,则其状态从当前q0转变为q(a)。
对于给定的的模式P=ababaca,首先定义一个函数f()为P的后缀函数,满足f(x)是x的后缀是P的最长前缀,
举个栗子:
f(ccaca)=1 x=ccaca,是x的后缀同时是P的最长前缀的是字符a,所以
f(ccaca)=1
同理f(ccab)=2
定义转移函数g(q,a):q为任意状态和字符a,则定义如下
g(q,a)=f(Pqa);记录当前状态q与当前字符a时已得到的与模式P匹配的文本字符串T的最长前缀。
原理:
自动机处于状态q并且读入下一个字符T[i+1]=a,那么此时这个状态转换是Tia的后缀,同时是P的最长前缀,记为f(Tia)。
T=abababacaba,P=ababaca
此时T中的字符为a,b,c这三种,那么对于状态从0开始,加入从T中读入a,则f(T1a)=1,T1a=a,T1a的后缀为P的最长前缀=a;假如读取字符为b/c,
则T1b/c的后缀为b/c,同时又是P的最长前缀的字符没有,状态为0
所以state 0=1,0,0
对于state=1,从T2中读取a,则T2a=aa,是T2a的后缀同时又是P的最长前缀=a,f(T2a)=1;假如读取字符为b,则T2a=ab,是T2a的后缀同时又是P的最长前缀=ab,所以f(T2a=b)=2,同理假如读取字符为c,则ac后缀与P的最长前缀为空,f(T2a=c)=0
依次推算,可以理解状态转移表中内容。
由上可知有两种情况:
第一种情况 a=P[q+1],使字符a可以继续匹配,那么可以沿着自动机主线(图中灰色部分)继续进行
第二种情况:a!=P[q+1],此时我们需要找到一个更小的子串,满足它是Tia的后缀同时是P的最长前缀。如f(5,b)=4,是因为状态q=5时读取字符b
此时T5a=ababab,P=ababaca,是T5a的后缀同时又是P的最长前缀=abab,所以f(5,b)=4.
对于Tia的后缀,同时是P的最长前缀下图可以理解
设Tia=ababcab P=abaca

即Tia从后往前与P的最大交集(这样解释虽然不科学)
理解了这个过程,则程序如下:
#include
#define MAX_LEN 100
#define MAX_CHAR 4
int state[MAX_LEN][MAX_CHAR];
int Prefix_cmp(char *P,int k,int q, char a) //求后缀
{
if(k==0)
return 1;
if(k==1)
{
return P[k-1]==a;
}
return P[k-1]==a&&(strncmp(P,P+q-k+1,k-1)==0);
}
void COMPUTE_TRANSITION_FUNCTION(char *P,char *A)//计算转移函数
{
int m,q,k,i;
m = strlen(P);
k = 0;
printf("%d \n",m);
for(q=0;q<=m;++q)
{
for(i=0;i1 ;++i)
{
k=min(m+1,q+2);
do
{
k=k-1;
}while(!Prefix_cmp(P,k,q,A[i]));//循环直至找出k,使Pk是(Pq+a)的最大后缀
state[q][i]=k;
printf("%d|%d ",k,q);
printf("%s\n",P);
}
}
printf("\n");
for(i=0;i<=m;++i)
{
for(q=0;q1;q++)
printf("(%d)%d ",i,state[i][q]);
printf("\n");
}
}
void FINITE_AUTOMATON_MATCHER(char *T,char *P,char *A) //根据转移函数匹配字符串
{
int n,m,i,q;
n=strlen(T);
m=strlen(P);
q=0;
COMPUTE_TRANSITION_FUNCTION(P,A);
for(i=0;i'a'];
if(q==m)
printf("%d\n",i-m);
}
}
int main() {
char T[MAX_LEN],P[MAX_LEN],A[MAX_CHAR];
scanf("%s",A);
scanf("%s",P);
scanf("%s",T);
FINITE_AUTOMATON_MATCHER(T,P,A);
return 0;
} 四:KMP算法
理解KMP算法,首先得理解PI数组的作用。
以朴素字符串的匹配过程为例:

如图所示:在模式P匹配文本T时,当匹配到最后一位不匹配时,朴素字符串匹配的做法是P往前移动一位继续匹配:

可是根据我们的观察发现更有效的做法是P可以直接往前移动两位,如下
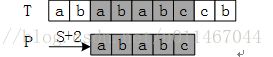
如上个人理解PI数组主要记录当前匹配无效时下次的有效偏移位数,避免无效的偏移。
KMP算法充分利用已匹配的信息,避免重复的匹配过程。
计算PI数组需要有效自动机中前缀与后缀的概念。
对于字符串abcd,则d,cd,bcd为其后缀,a,ab,abc为其前缀。
KMP的理解点一在于 PI 数组的求解,二在于利用PI数组进行匹配
PI数组的求解:

算法导论中伪代码如上:
对于PI数组的值可以理解为前后缀的匹配,在上述伪代码中,对于PI[1]=0,是因为一个字符,既无后缀,又无前缀。
从5-10行for循环的迭代开始,while循环搜索k(PI数组)的值,直至找到一个k的值,使得P[k+1]=P[q]。
(由算法导论引理32.5与引理32.6可知,k必定在转移函数PI数组中)
8-9行代码实现了PI值得调整,取得前缀是其最大后缀。(引理32.7)。
KMP算法的精髓如下:

KMP的伪代码如下:


这两段代码思想完全相同,如果和前缀不同就比较前缀的前缀
基于C语言实现如下:
#includewhile((k>0)&&P[k]!=P[q])
{
//q=PI[q];
k=PI[k];
}
if(P[k]==P[q])
k=k+1;
PI[q]=k;
}
}
void KMP_matcher(char T[],char P[])
{
int n,m,q,i;
n=strlen(T);
m=strlen(P);
Compute_prefix_fun(P);
q=0;
for(i=0;iwhile((q>0)&&P[q]!=T[i])
{
q=PI[q-1];
}
if(P[q]==T[i])
q=q+1;
if(q==m)
{
printf("%d\n",i-m+1);
q=PI[q-1];
}
}
}
int main()
{
char T[20],P[20];
scanf("%s",T);
scanf("%s",P);
KMP_matcher(T,P);
return 0;
} 