快排算法
最近在看算法导论，第七章讲的是快排算法。
本篇文章使用c++来实现：
常规算法
书中的伪代码如下：
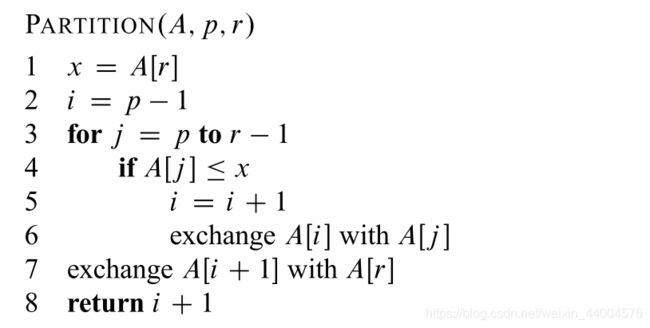快排的核心思想是找出一个分割数组的元素，在小于该元素的数组索引对应的元素值小于该值，在大于该元素的索引的数组元素大于该值。当然等于也是可以的。本文是跟书中一致，选择数组中最后一个元素作为对比对象。
代码如下：
template<typename T>
void exchange(T& l, T& r)
{
T tmp = l;
l = r;
r = tmp;
}
template <typename T>
size_t partition(vector<T>& input, int p, int r)
{
T x = input[r];
int i = p - 1;
for (int j = p; j < r ; j++)
{
if (input[j] <= x)
{
i++;
exchange<T>(input[i], input[j]);
}
}
exchange<T>(input[i+1], input[r]);
return i + 1;
}
template <typename T>
void quick_sort(vector<T> &input, int p, int r)
{
if (p < r)
{
if (r == (p + 1))
{
if (input[p] > input[r])
exchange(input[p], input[r]);
}
else
{
int q = partition(input, p, r);
quick_sort<T>(input, p, q - 1);
quick_sort<T>(input, q + 1, r);
}
}
}
代码说明：
快排算法中的partition函数，主要的目的在于确定数组中，最后一个元素的最终索引位置。边界条件的选择很重要，我使用的方法是元素分别为1,2,3,4个，测试边界条件来调制出来的，所以跟伪代码不完全相同。
加入随机化采样的快排算法
随机化算法的思想就是常规算法将序列的最后一个元素作为分界，但是分析快排算法发现其实快排对大多数的情况都能满足平均的时间复杂度，这就意味着增加随机性，可以让排序渐进满足平均的时间复杂度！
所以这个算法选择就是在序列的区间中，等概率的选择一个与最后一个元素交换，然后就是常规的计算过程。
实现的代码如下：
template <typename T>
int random_partition(vector<T>& input, int p, int r)
{
std::random_device rd;
std::mt19937 gen(rd());
std::uniform_int_distribution<> dis(p, r);
int i = dis(gen);
exchange(input[i], input[r]);
return partition<T>(input, p, r);
}
template <typename T>
void random_quick_sort(vector<T> &input, int p, int r)
{
if (p < r)
{
if (r == (p + 1))
{
if (input[p] > input[r])
exchange(input[p], input[r]);
}
else
{
int q = random_partition(input, p, r);
quick_sort<T>(input, p, q - 1);
quick_sort<T>(input, q + 1, r);
}
}
}
就加了一个随机选择交换的部分。
测试代码：
void test_random_quick_sort()
{
vector<int> v = {
2,2,7,1,3,5,6,4 };
//quick_sort(v, 0, 7);
random_quick_sort<int>(v, 0, 7);
for (auto x : v)
{
cout << x << endl;
}
}
在课后题7.5中提出一种median_3算法，基本思想是在随机化的时候，为了更能反映更广泛的意义的抽样，随机抽样三次，选择元素的中位数作为划分基准，跟数组最后面的元素交换
代码如下（里面使用了标准库的容器）：
template <typename T>
int random_median_partition(vector<T>& input, int p, int r)
{
std::random_device rd;
std::mt19937 gen(rd());
std::uniform_int_distribution<> dis(p, r);
vector<int> tmp_index;
vector<T> tmp_data;
for (int i = 0; i < 3; i++)
{
tmp_index.push_back(dis(gen));
tmp_data.push_back(input[tmp_index[i]]);
}
int index;
if (tmp_data[0] >= tmp_data[1] && tmp_data[1] >= tmp_data[2])
index = tmp_index[0];
else if (tmp_data[1] >= tmp_data[0] && tmp_data[1] >= tmp_data[2])
index = tmp_index[1];
else
index = tmp_index[2];
exchange(input[index], input[r]);
return partition<T>(input, p, r);
}
template <typename T>
void random_median_quick_sort(vector<T> &input, int p, int r)
{
if (p < r)
{
if (r == (p + 1))
{
if (input[p] > input[r])
exchange(input[p], input[r]);
}
else
{
int q = random_median_partition(input, p, r);
quick_sort<T>(input, p, q - 1);
quick_sort<T>(input, q + 1, r);
}
}
}
测试代码如下：
void test_random_median_quick_sort()
{
vector<int> v = {
2,2,7,1,3,5,6,4 };
//quick_sort(v, 0, 7);
random_median_quick_sort<int>(v, 0, 7);
for (auto x : v)
{
cout << x << endl;
}
}