（十三）从零开始学人工智能-强化学习:值函数近似和策略梯度

强化学习–值函数近似和策略梯度

前两节内容都是强化学习的一些基础理论 ，只能解决一些中小规模的问题，实际情况下很多价值函数需要一张大表来存储，获取某一状态或动作价值的时候通常需要一个查表操作，这对于某些状态或动作空间很大的问题几乎无法求解，而许多实际问题拥有大量状态或动作，甚至是连续的状态和动作。那么，如何解决实际问题呢？主要有两种方法：值函数近似和策略梯度。

1. 值函数近似

强化学习可以用来解决大规模问题，例如西洋双陆棋（Backgammon）有$10^{20}$个状态空间，围棋AlphaGo有$10^{170}$状态空间，机器人控制以及无人机控制需要的是一个连续状态空间。如何才能将强化学习应用到这类大规模的问题中，进而进行预测和控制呢？

（1）使用值函数近似的解决思路可以是这样的：

①、通过函数近似来估计实际的价值函数：
$$\hat{v}(s,\omega )\approx v_{\pi }(s)$$

$$\hat{q}(s,a,\omega )\approx q_{\pi }(s,a)$$

其中，$\omega$表示函数的参数，如神经网络的参数；

②、把从已知状态学到的函数通用化推广到那些未碰到的状态中；

③、使用蒙特卡洛算法或时序差分学习来更新函数参数。

（2）值函数近似的类型：

①、针对状态，输出这个状态的近似状态价值；

②、针对状态动作对，输出状态动作对的近似动态价值；

③、针对状态，输出一个向量，向量中每一个元素是该状态下采取一种可能动作的动作价值；注：此时不能用于连续的动作。

（3）有哪些函数近似器？

所有和机器学习相关的算法都可以应用到强化学习中来，其中线性回归和神经网络在强化学习里应用比较广泛，主要是因为这两类方法针对状态可导。

强化学习应用的场景其数据通常是非静态的（non-stationary）和非独立同分布（non-iid）的，因为一个状态数据是可能是持续流入的，而且下一个状态通常与前一个状态是高度相关的。因此，函数近似器也需要适用于非静态、非独立同分布的数据。

注：iid: independent and identically distributed 独立和均匀分布

独立：每次抽样之间是没有关系的，不会相互影响；就像抛骰子每次抛到几就是几这就是独立的，但如果要两次抛的和大于8，其余的不算，那么第一次抛和第二次抛就不独立了，因为第二次抛的时候结果是和第一次相关的。

同分布：每次抽样，样本都服从同样一个分布；抛骰子每次得到任意点数的概率都是1/6，这就是同分布的。但如果第一次抛一个6面的色子，第二次抛一个正12面体的色子，就不再是同分布了。

（4）值函数近似的目标：

寻找参数向量$\omega$，从而最小化近似值函数$\hat{v}(s,\omega )$和真实的值函数$v_{\pi }(s)$的均方误差（mean squared error，MSE）:
$$J(\omega )=E_{\pi }[(v_{\pi }(S)-\hat{v}(S,\omega ){)}^2]$$
然后使用随机梯度下降对梯度进行更新。每一步，参数朝着实际的价值函数进行一度程度地逼近。

1.1 线性函数近似

1.1.1 状态价值函数近似

用一个特征向量表示一个状态：
$$x(S)=\left(\begin{array}{l}{x}_1(S)\\ ⋮\\ x_n(S)\end{array}\right)$$
通过对特征的线性求和来近似状态价值函数：
$$\hat{v}(S,\omega )=x(S{)}^T\omega =\sum _{j=1}^n{x}_j(S){\omega }_j$$
这样，目标函数可以表示为：
$$J(\omega )=E_{\pi }[(v_{\pi }(S)-x(S{)}^{\top }\omega {)}^2]$$
使用随机梯度下降可以收敛至全局最优解。

参数更新规则比较简单：
$${\nabla }_{\omega }\hat{v}(S,\omega )=x(S)$$

$$\Delta \omega =\alpha (v_{\pi }(S)-\hat{v}(S,\omega ))x(S)$$

即：参数更新量=步长*预测误差*特征值；

“查表”方法是一个特殊的线性价值函数近似方法：每一个状态看成一个特征，个体具体处在某一个状态时，该状态特征取1，其余取0。参数的数目就是状态数，也就是每一个状态特征有一个参数。

事实上，之前所列的公式都不能直接用于强化学习，因为公式里都有一个实际价值函数$v_{\pi }(S)$，但在强化学习环境中，只有即时奖励，没有真实的价值函数，因此不能直接使用上述公式，需要找到能代替$v_{\pi }(S)$的目标值。

①、对于蒙特卡洛算法，目标值就是回报：
$$\Delta \omega =\alpha (G_t-\hat{v}(S_t,\omega )){\nabla }_{\omega }\hat{v}(S_t,\omega )$$
其中，回报$G_t$是真实状态价值的无偏估计，可以把它看成是监督学习的标签数据，这时，训练数据集可以是：$<S_1,G_1>,<S_2,G_2>,...,<S_T,G_T>$；

②、对于时序差分学习，目标值就是TD目标：
$$\Delta \omega =\alpha (R_{t+1}+\gamma \hat{v}(S_{t+1},\omega )-\hat{v}(S_t,\omega )){\nabla }_{\omega }\hat{v}(S_t,\omega )$$
其中，TD目标值是真实状态价值的有偏估计；这时，训练集是：$<S_1,R_2+\gamma \hat{v}(S_2,\omega )>,<S_2,R_3+\gamma \hat{v}(S_3,\omega )>...,<S_{T-1},R_T>$；

1.1.2 动作价值函数近似

动作价值函数近似和上述状态价值函数近似类似。

动作价值函数近似表示为：
$$\hat{q}(S,A,\omega )\approx q_{\pi }(S,A)$$
用一个特征向量表示一个状态动作对：
$$x(S,A)=\left(\begin{array}{l}{x}_1(S,A)\\ ⋮\\ x_n(S,A)\end{array}\right)$$
通过对特征的线性求和来近似动作价值函数：
$$\hat{q}(S,A,\omega )=x(S,A{)}^T\omega =\sum _{j=1}^n{x}_j(S,A){\omega }_j$$
这样，目标函数可以表示为：
$$J(\omega )=E_{\pi }[(q_{\pi }(S,A)-x(S,A{)}^{\top }\omega {)}^2]$$
使用随机梯度下降可以收敛至全局最优解。

参数更新规则比较简单：
$${\nabla }_{\omega }\hat{q}(S,A,\omega )=x(S,A)$$

$$\Delta \omega =\alpha (q_{\pi }(S,A)-\hat{q}(S,A,\omega ))x(S,A)$$

同样，需要找到能代替$q_{\pi }(S,A)$的目标值。

①、对于蒙特卡洛算法，目标值就是回报：
$$\Delta \omega =\alpha (G_t-\hat{q}(S_t,A_t,\omega )){\nabla }_{\omega }\hat{q}(S_t,A_t,\omega )$$
其中，回报$G_t$是真实动作价值的无偏估计；

②、对于时序差分学习，目标值就是TD目标：
$$\Delta \omega =\alpha (R_{t+1}+\gamma \hat{q}(S_{t+1},A_{t+1},\omega )-\hat{q}(S_t,A_t,\omega )){\nabla }_{\omega }\hat{q}(S_t,A_t,\omega )$$
其中，TD目标值是真实动作价值的有偏估计；

在上一讲中，我们讲到，在无模型情况下，对策略评估时，使用状态动作对下的动作价值函数对策略进行评估。

从一系列参数开始，得到一个在状态动作对下近似的动作价值函数，在$ϵ-greedy$策略下产生一个动作，执行该动作得到一个即时奖励，以此数据计算目标值，进行近似函数参数的更新，再利用这个策略得到后续的状态和对应的目标值，每经历一次状态就更新一次次数，如此反复进行策略的优化，同时逼近最优价值函数。

策略评估：使用动作价值函数近似方法来进行近似策略评估，特别是早期误差会较大，而且这种近似无法最终收敛于最优策略对应的行为价值函数，只能在其周围震荡；

策略改善：使用$ϵ-greedy$策略。

1.2 深度神经网络近似

在计算机视觉、语音识别领域，深度神经网络可以直接从场景数据（如图像，声音）中提取出高层特征，实现端到端的学习，无需再人工设计特征。一个自然的想法时能否用深度学习来为强化学习的原始输入数据进行建模。

深度强化学习的基本思想是用神经网络拟合强化学习中的价值函数和策略函数，是深度学习与强化学习相结合的产物。在这里，讲到的使用深度神经网络对价值函数进行近似的方法称为基于价值函数的深度强化学习。

用深度神经网络来近似动作价值函数$Q$时，网络的输入为状态数据，如原始的游戏画面，输出值为在当前状态下执行各种动作所得到的最大$Q$函数值。但是深度学习用于强化学习将面临以下挑战：

①、有监督学习一般要求训练样本之间是相互独立的，在强化学习中，经常遇到的是前后高度相关的状态序列。在某个状态下执行一个动作后进入下一个状态，前后两个状态存在着明显的概率关系，不是独立的；

②、在强化学习中，随着学习到新的动作，样本数据的概率分布会发生变化，而在深度学习中，要求训练样本的概率分布是固定的；

即深度学习中一般要求样本满足独立同分布，而强化学习不满足。

2013年，DeepMind公司提出了一种用深度神经网络打Atari游戏的方法，仅通过观察游戏画面和得分，就可以学会打这种游戏。该方法使用深度卷积神经网络拟合动作价值函数，即$Q$函数，成为深度$Q$网络（DQN），它是第一个成功具有通用性的深度强化学习算法。

早在1995年，人们就开始尝试将神经网络与强化学习进行结合，比如当时Gerald Tesauro提出的TD-gammon方法，用多层感知器模型逼近状态价值函数，然而，此时只对西洋双陆棋有较好的效果，对于国际象棋等效果非常差，不具有通用性。

关于Atari游戏示例：

接下来主要讲一下DQN。

网络的输入为经过处理后的若干帧游戏图像画面，输出为在这种状态下执行各种动作的动作价值函数，即$Q$函数。

输入输出有两种形式：

①、将状态和动作当成神经网络的输入，然后输出状态动作对对应的$Q$值；

②、只输入状态值，输出所有动作值对应的$Q$值；

这里，采用的是第②种方法，因为如果按第①种方法输入状态动作对的话，神经网络的每一次前向传播只是来计算一个动作的$Q$值，导致成本会随动作数量而线性增加。而采用第②种方法，能够计算给定状态下所有可能动作的$Q$值且只需要通过网络进行一次前向传播，提高了计算效率。

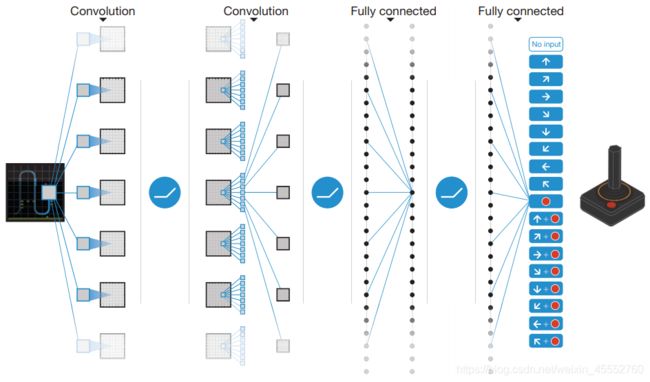
DQN的网络架构如下所示：

在图中，输入的是经过处理的84*84的游戏图像画面，然后经过2个卷积层，2个全连接层，最后网络的输出是在输入状态下执行每个动作的$Q$函数值。

卷积神经网络用于近似最优$Q$函数：
$$Q(S,A,\omega )\approx Q_{\pi }(S,A)$$
其中，$\omega$是网络参数。

对于网络结构，针对不同的问题可以有不同的设置。

总之，用神经网络来表示$Q$值非常简单，$Q$值也就是变成$Q$网络来表示。

那么，怎么训练$Q$网络呢？

神经网络的训练是一个最优化问题，最优化一个损失函数，也就是标签和网络输出的偏差，目标是让损失函数最小化。因此，需要有样本，即大量有标签的数据，然后通过反向传播使用梯度下降的方法来更新网络参数。

所以，要训练$Q$网络，要能够为$Q$网络提供有标签的样本。

那么，问题变为：如何为$Q$网络提供有标签的样本？

答案是利用$Q-learning$算法，依靠的是目标$Q$值，即即时奖励和其后继状态执行动作的最大$Q$值：
$$R_{t+1}+\lambda \underset{a}{\max }Q(S_{t+1},a)$$
所以，可以目标$Q$值当作标签。那么，损失函数是：
$$L(\omega )=E[(R+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime },\omega )-Q(s,a,\omega ){)}^2]$$
其中，$s^{\prime },a^{\prime }$分别是下一个状态和动作。

DQN的一个创新是使用了经验回放（Experience Replay）机制。

①、动机：深度神经网络作为有监督学习模型，要求数据满足独立同分布，而Atari游戏得到的训练样本是一个时间序列，样本之间存在相关性，而且训练样本的概率分布不固定，为了解决上述问题，提出了经验回放机制。

②、具体做法：在每个时间点存储智能体的经验$e_t=(s_t,a_t,r_{t+1},s_{t+1})$形成回放记忆序列$D=e_1,...,e_N$，将这些数据存储起来，训练神经网络时从$D$中随机采样得到每次迭代所用的训练样本，并使用随机梯度下降算法更新网络参数。

③、作用：经验回放机制通过重复采样历史数据增加了数据的使用效率，同时打破按照动作序列执行时前后两个时间步样本之间的依赖关系，即减少了数据之间的相关性。

DQN算法伪代码：

在上述DQN中，每次迭代时$Q$值与$Q-learning$的目标值（目标$Q$值）之间存在相关性，因为它们由同一个$Q$网络预测产生。因此，在2015年，2013年提出DQN的Volodymyr Mnih等人为消除上述的相关性，对DQN进行了改进，提出了固定$Q$函数的策略，即使用另外一个$Q$网络（称为目标$Q$网络）来计算训练时的目标函数值，目标$Q$网络周期性地与$Q$网络进行同步。

DQN方法的其他改进：

在这里就不对这些改进方法进行一一介绍了，有兴趣的可以查看相关论文。

2. 策略梯度

上面见了对价值函数进行近似的参数化表达，包括状态价值函数和动作价值函数，随后一个策略可以直接从价值函数中产生，比如使用$ϵ-greedy$探索方法。但是，如果动作集合是连续的或维数很高，这种方法将面临问题。

这时，可以直接参数化策略本身，同时参数化的策略将不再是一个概率集合而是一个函数：
$${\pi }_{\theta }=P[a|s,\theta ]$$
策略函数确定了在给定的状态和一定的参数设置下，执行任何可能动作的概率，事实上它是一个概率密度函数。在实际应用策略产生动作时，是按照这个概率分布进行动作采样的。策略函数里的参数决定了概率分布的形态。

目的是利用参数化的策略函数，通过调整这些参数来得到一个较优策略，遵循这个策略产生的行为将得到较多的奖励。具体的机制是设计一个目标函数，对其使用梯度上升（Gradient Ascent）算法优化参数以最大化奖励。

（1）目标函数

目标：用一个参数$\theta$建模策略${\pi }_{\theta }(s,a)$，寻找最优的参数$\theta$。

但是，如何寻找呢？

值函数近似时，优化的目标是使值函数的输出接近目标值。

策略梯度算法是通过最大化回报逼近最优策略。

因此，我们需要设计一个目标函数来评估策略的好坏。

针对不同的问题类型，有3种典型的目标函数：

①、Start Value

要有起始状态，并且能够得到完整的episode，即在有限步之后能到达终止状态。根据当前的策略函数执行动作可以得到的一个完整的episode，然后计算这个episode的累计回报值：
$$J_1(\theta )=V^{{\pi }_{\theta }}(s_1)=E_{{\pi }_{\theta }}[v_1]$$
②、Average Value

对于连续环境条件，不存在一个起始状态，，此时计算状态价值的数学期望：即考虑智能体在某时刻处在某状态下的概率，也就是智能体在该时刻的状态分布，针对每个可能的状态计算从该时刻开始一直持续与环境交互下去能够得到的奖励，按该时刻各状态的概率分布求和：
$$J_{av}v(\theta )=\sum _s{d}^{{\pi }_{\theta }}(s)V^{{\pi }_{\theta }}(s)$$
其中，$d^{{\pi }_{\theta }}$是在当前策略下，马尔可夫链关于状态的一个静态分布（stationary distribution），可以理解为状态$s$出现的概率。

③、Average Reward Per Time-Step（单步平均回报）

每执行一个动作的立即回报的均值，即在各种状态时，执行各种动作的回报的概率求和。

也就是说：在某一时刻，首先得到智能体处于所有状态的可能性;

然后每一种状态下执行所有动作能够得到的即时奖励

最后所有奖励按概率求和。

$$J_{av}R(\theta )=\sum _s{d}^{{\pi }_{\theta }}(s)\sum _a{\pi }_{\theta }(s,a)R_s^a$$

其实上述三个式子的目标都是同一个目标，都是试图描述（衡量）智能体在某一时刻的价值。

（2）目标函数优化

确定了目标函数之后，接下来就是优化策略参数使得目标函数值最大化；也就是得到一组参数向量$\theta$，使得目标函数最大。如果策略函数可到，则可以根据样本计算目标函数的梯度值，用梯度上升法（因为要求目标函数的极大值，因此，要将梯度下降改为梯度上升）更新策略函数的参数。此时，问题的关键就变成了如何计算目标函数对策略参数的梯度值。

策略梯度定理：

对于一个可导的策略函数${\pi }_{\theta }$，无论采用上述三种定义的哪种目标函数，策略的梯度都可以写为：
$${\nabla }_{\theta }J(\theta )=E_{{\pi }_{\theta }}[{\nabla }_{\theta }log{\pi }_{\theta }(s,a)Q^{{\pi }_{\theta }}(s,a)]$$
其中，定义${\nabla }_{\theta }log{\pi }_{\theta }(s,a)$为score函数。

（3）策略函数的构造

策略函数的构造对离散动作和连续动作有不同的处理。

①、对于离散型动作，策略函数给出的是执行每个动作的概率，所有动作的概率之和为1。这可以看成是多分类问题，根据输入的状态确定要执行的动作的类型。通常采用Softmax策略。

使用Softmax策略时，可以把动作看成是多个特征在一定权重下的线性代数和：$\varphi (s,a{)}^{\top }\theta$；

然后执行某一具体动作的概率为：
$${\pi }_{\theta }(s,a)=\frac{{e^{\varphi (s,a)}}^{\top }\theta }{\sum _b{e}^{\varphi (s,b{)}^{\top }\theta }}$$
②、对于连续型动作，无法将所有的动作都列举出来，输出执行每个动作的概率值，只能得到动作的概率密度函数。在运行时，动作参数根据概率分布采样得到，即生成服从此分布的一个随机数作为最后的动作参数。通常采用高斯策略。

使用高斯策略时，通常对于均值有一个参数化表示，可以是一些状态特征的线性代数求和：
$$\mu (s)=\varphi (s{)}^{\top }\theta$$
方差可以是固定值${\sigma }^2$，也可以参数化表示。

动作对应于某一个具体的数值，该数值从以均值为$\mu (s)$，标准差为$\sigma$的高斯分布中随机采样产生：
$$a\sim N(\mu (s),{\sigma }^2)$$
（4）蒙特卡洛策略梯度

针对具有完整episode的情况，应用策略梯度定理，使用随机梯度上升来更新参数，然后通过采用的方式，使用$t$时刻的回报作为当前策略下动作价值的无偏估计。

算法过程是这样的：

①、随机初始化策略函数的参数$\theta$；

②、对当前策略下的一个episode：
$$\{s_1,a_1,r_2,...,s_{T-1},a_{T-1},r_T\}\sim {\pi }_{\theta }$$
从$t=1$到$t=T-1$间的每一个时刻，计算智能体获得的回报；

③、使用随机梯度上升更新参数$\theta$；

④、重复每一个episode，直到结束。

伪代码如下所示：

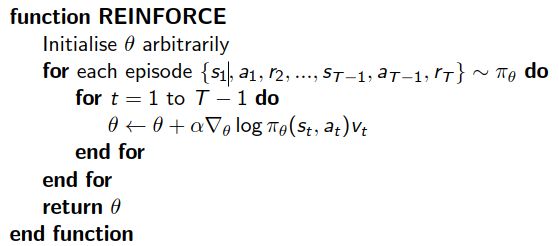
（5） Actor-Critic算法

虽然Actor-Critic算法里用到了价值函数的近似，但是，其核心还是策略梯度，所以直接在该策略梯度章节里讲。

Actor-Critic的字面意思是“演员-评论”，相当于演员在演戏的同时有评论家指点继而演员演得越来越好。

Actor-Critic包含两部分：

①、Actor：策略函数，负责产生动作；以Critic所指导的方向更新策略参数$\theta$；

②、Critic：价值函数，负责评价Actor产生的动作的好坏；更新动作价值函数参数$\omega$；

Actor-Critic的网络结构图如下：

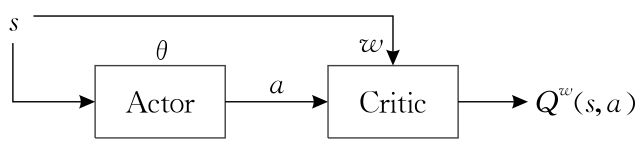
大致流程是：

①、Actor根据目前的状态，输出一个动作，

②、Actor输出的状态和动作一起输入到Critic中，Critic如时序差分学习的策略评价方法，通过估计动作价值函数来对Actor输出的动作进行评价，并更新参数$\omega$；

③、Actor根据Critic输出的动作价值函数，来更新自己的策略${\pi }_{\theta }(s)$的参数$\theta$；

这里给一个Actor-Critic的算法流程总结，Critic使用神经网络计算TD误差并更新网络参数，Actor也使用神经网络来更新网络参数。

算法输入：迭代轮数$T$，状态特征维度$n$，动作集$A$, 步长$\alpha ,\beta$，衰减因子$\gamma$，探索率$ϵ$，Critic网络结构和Actor网络结构；

输出：Actor 网络参数$\theta$，Critic网络参数$\omega$；

1、随机初始化所有的状态和动作对应的价值$Q$， 随机初始化Critic网络的所有参数$w$。随机初始化Actor网络的所有参数$\theta$。

2、for $i$ from 1 to $T$，进行迭代。

​ a) 初始化$S$为当前状态序列的第一个状态，得到其特征向量$\varphi (S)$；

b) 在Actor网络中使用$\varphi (S)$作为输入,输出动作$A$，基于动作$A$得到新的状态$S\prime$，即时奖励$R$；

c) 在Critic网络中分别使用$\varphi (S),\varphi (S^{\prime })$作为输入，得到$Q$值输出$V(S),V(S^{\prime })$；

​ d) 计算TD误差$\delta =R+\gamma V(S^{\prime })-V(S)$；

e) 使用均方差损失函数$\sum {(R+\gamma V(S^{\prime })-V(S,\omega ))}^2$作Critic网络参数$\omega$的梯度更新；

​ f) 更新Actor网络参数$\theta$ :
$$\theta =\theta +\alpha {\nabla }_{\theta }log{\pi }_{\theta }(S_t,A)\delta$$
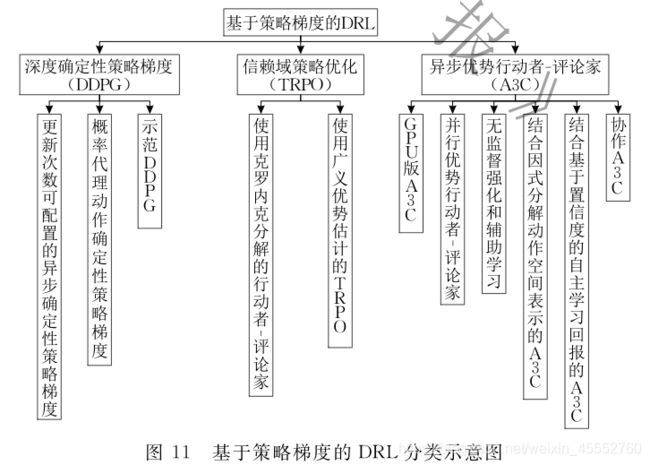
（6）基于梯度策略的DRL分类

基于梯度策略的DRL分类如下：

在这里就不对各个方法进行一一介绍了，有兴趣的可以查看相关论文。

声明

本博客所有内容仅供学习，不为商用，如有侵权，请联系博主，谢谢。

参考资料

[1] David Silver强化学习公开课

[2] David Silver强化学习公开课中文讲解

[3] 机器学习原理、算法与应用，雷明

[4] 人工智能：一种现代的方法（第3版）

[5] An Introduction to Reinforcement Learning

[6] Algorithms for Reinforcement Learning

[7] 经验回放（Experience replay）

[8] 基于值函数和策略梯度的深度强化学习综述，计算机学报，刘建伟、高峰、罗雄麟

[9] Playing Atari with Deep Reinforcement Learning，2013

[10] Human-level control through deep reinforcement learning，2015

[11] Actor-Critic

] 人工智能：一种现代的方法（第3版）

[5] An Introduction to Reinforcement Learning

[6] Algorithms for Reinforcement Learning

[7] 经验回放（Experience replay）

[8] 基于值函数和策略梯度的深度强化学习综述，计算机学报，刘建伟、高峰、罗雄麟

[9] Playing Atari with Deep Reinforcement Learning，2013

[10] Human-level control through deep reinforcement learning，2015

[11] Actor-Critic