【C语言->数据结构与算法】->巨大数的加减乘->万进制的运用及神奇的微易码补码
巨大数
-
- Ⅰ 巨大数的概念
- Ⅱ 巨大数的意义
- Ⅲ 分析
- Ⅳ *** 万进制的介绍和分析
- Ⅴ 巨大数的构建
- Ⅵ 初始化 及 输出
- Ⅶ 销毁
- Ⅷ 倒置
- Ⅸ *** 微易码补码
- Ⅹ 将数据编码 及 解码
- ⅩⅠ *** 微易码补码实现加法和减法
- ⅩⅡ *** 用多项式思想实现乘法
- ⅩⅢ 完整代码
Ⅰ 巨大数的概念
所谓巨大数,就是字面意思所指的非常大的数,大到C语言中无法表示出来,更不能计算。
Ⅱ 巨大数的意义
IT界有一个著名的问题,千年虫问题。
计算机2000年问题,又叫做“千年虫”、“电脑千禧年千年虫问题”或“千年危机”。缩写为“Y2K”。是指在某些使用了计算机程序的智能系统(包括计算机系统、自动控制芯片等)中,由于其中的年份只使用两位十进制数来表示,因此当系统进行(或涉及到)跨世纪的日期处理运 算时(如多个日期之间的计算或比较等),就会出现错误的结果,进而引发各种各样的系统功 能紊乱甚至崩溃。因此从根本上说千年虫是一种程序处理日期上的bug(计算机程序故障),而非病毒。
同样情况,C语言中能表示的数字也是有限的,比如int型,只能表示-2147483648 ~ 2147483647,因为int型常量的本质是4字节补码,也就是32位补码,当数值超过了2^31 - 1 时(补码的首位为符号位),该值就会变成负数。我们在此做一下验证。
我们先将值设为极限值。
#include 
可以看到,是可以正常输出2147483647的。
当num大于这个值时
#include 我们只将num加了个1,结果如下:

这就是int型的本质,是一个32位的补码。感兴趣或者不相信的同学可以自行验证。
所以同int类型一样,C语言中最大的类型是8字节,但也至此为止了。因此若要计算更大的数值,我们需要使用巨大数。
Ⅲ 分析
我们首先要考虑的是,如何接收一个巨大数?
我们已经论证过了,各种整形量是不行的,所以只有一个方法,即字符串。所以现在我们只需要考虑的是,如何将字符串变成数字,然后进行运算。
在老师没有提示之前,我用的是最笨的方法,即将两个字符串一位一位比较然后运算,但这个方法如果数字足够多,比如一个几百位的巨大数,再一位一位进行运算,效率是很低的,所以在此我引入一个概念——万进制
Ⅳ *** 万进制的介绍和分析
万进制,即以0-9999为基本单位,当数值变成10000时,向下一位进1。就和我们熟悉的2进制,8进制一样,万进制是个更大的数字变化规则,但本质都是一样的。以此存储接收的字符串,即四个数字为一组,存储到数组中。这样,我们不必进行一位一位的运算,而是可以直接进行四位四位的运算,运算效率获得了极大的提高。
但既然要提高效率,为什么不能五个数字八个数字一起计算,用十万进制甚至百万进制呢?原因就是乘法。万进制不只是要为我们的加减法服务,我们还要做乘法,当五位相乘的时候,结果是可以超过21亿的,也就是超过了int型能表示的最大值,我们本来就是要计算巨大数,结果却制造了更多的巨大数,南辕北辙。
因此万进制是在保证稳定可以运算的情况的基础下,能有的最方便的进制单位。
Ⅴ 巨大数的构建
根据之前的分析,巨大数需要用数组储存,我们肯定不能用静态数组,因为在用户输入之前,我们并不知道会需要多少空间来储存。因此使用动态存储类。根据用户输入的字符串,我们需要得到字符串的位数,以此来判断动态数组所需要的空间大小,以及该数的符号。因此最合适的数据结构是结构体。
typedef struct HUGE_NUMBER {
boolean sign; //符号
int count; //有效数字位数
int *number; //万进制数组
}HUGE_NUMBER;
boolean是我在常用的自己的头文件中定义的一个数据类型,本质是unsigned char,数据的正负我们遵从补码的模式,1为负,0为正。
Ⅵ 初始化 及 输出
初始化
在接收一个字符串后,首要任务便是要初始化这个结构体,因此我们先构建一个初始化的函数,将接收的字符串的有效数字位数和符号保存,并将其转换成万进制。代码如下:
boolean init(char *item, HUGE_NUMBER *hugeNumber) {
boolean sign;
char temp[4] = {
0};
int i;
int j;
int numberIndex = 0;
int count;
int figure;
int headFigure;
if ('-' == item[0]) {
sign = 1;
count = strlen(item) - 1;
} else {
sign = 0;
count = strlen(item);
}
figure = (count + 3) / 4;
headFigure = count - (figure - 1) * 4;
hugeNumber->sign = sign;
hugeNumber->count = count;
hugeNumber->number = (int *) calloc(sizeof(int), figure);
if (NULL == hugeNumber->number) {
return FALSE;
}
for (i = 0; i < headFigure; i++) {
if (1 == sign) {
temp[i] = item[i + 1];
} else {
temp[i] = item[i];
}
}
hugeNumber->number[numberIndex] = atoi(temp);
numberIndex++;
if (1 == sign) {
i = headFigure + 1;
} else {
i = headFigure;
}
while (i < count) {
for (j = 0; j < 4; j++) {
temp[j] = item[i];
i++;
}
hugeNumber->number[numberIndex] = atoi(temp);
numberIndex++;
}
return TRUE;
}
我们输入一串数字,比如32767, 要将其变成万进制就是 3 2767,由此可见,首位万进制并不一定就是四位数字,所以我将首位于其他位分开,计算出四位四位分开后,还余几位,余下来的位数便是首位万进制需要储存的数字位数,需要单独从字符串抓取,其余的四位四位从字符串中抓取。
在此函数中有一个需要注意的运算以及一个函数。
figure = (count + 3) / 4;
count为有效数字的位数,如果用户输入了一个负数,则count = strlen(字符串) - 1,figure为数组的元素个数,即万进制的位数,四个数字一位,根据这个式子就可以计算出所需要的位数,这种公式需要自己多加计算然后得出规律。
hugeNumber->number[numberIndex] = atoi(temp);
atoi()是一个将字符转成数字的函数,即ASCII to int,同样的还有itoa(),作用是反过来的,通过这个函数,我们将有效数字从字符串中抓取。
输出
完成初始化,我建议先做一个输出的函数,将数据输出,这样可以随时验证自己程序的正确与否,是否有正确的初始化。
代码如下:
void output(HUGE_NUMBER hugeNumber) {
int i;
int figure = (hugeNumber.count + 3) / 4;
if (NULL == hugeNumber.number) {
printf("输出错误\n");
return;
}
if (hugeNumber.sign == 1) {
printf("%c", '-');
}
printf("%d", hugeNumber.number[0]);
for (i = 1; i < figure; i++) {
printf("%04d", hugeNumber.number[i]);
}
}
Ⅶ 销毁
有了初始化,申请了空间,就一定要考虑释放空间,这个要构成编程的基本意识,释放的代码也很简单,在此不再赘述。代码如下:
void destory(HUGE_NUMBER *hugeNumber) {
if (NULL == hugeNumber->number) {
return;
}
free(hugeNumber->number);
}
Ⅷ 倒置
按之前的例子, 32767经过了初始化,变成了 3 2767,但是这样进行运算会很麻烦,因为无论是加减还是乘,我们都是从低位运算到高位,这样进位也很方便,退位也很方便,所以为了之后的运算,我们先完成一个倒置的函数,即将 3 2767变成 2767 3。代码如下:
void reverse(HUGE_NUMBER *hugeNumber) {
int i;
int figure = (hugeNumber->count + 3) / 4;
HUGE_NUMBER tempHugeNumber;
tempHugeNumber.count = hugeNumber->count;
tempHugeNumber.sign = hugeNumber->sign;
tempHugeNumber.number = (int *) calloc(sizeof(int), figure);
for (i = 0; i < figure; i++) {
tempHugeNumber.number[i] = hugeNumber->number[figure-i-1];
}
for (i = 0; i < figure; i++) {
hugeNumber->number[i] = tempHugeNumber.number[i];
}
free(tempHugeNumber.number);
}
这个函数也很简单,就是建立一个新的结构体作为中间站,从而将数组的元素倒置,只是不要忘记,我们需要将暂时申请的空间释放掉。
Ⅸ *** 微易码补码
接下来就到最玄妙的地方了,就是由我的老师朱洪先生独创的补码方式,由于本人能力不足,在此不做数学证明,只给定义以及使用方法。
我们先回顾补码和原码,比如(1001 0110)原,将其除符号位(1)外,按位取反,末位加1,得到补码,(1110 1010)补,这便是二进制的补码,引入其的原因是要用加法实现减法,原码补码的机制就很像钟表,钟表是不能逆行的,只能通过加来实现减。加法实现减法,这就是补码的意义。
所以微易码补码在此是为万进制服务的,其定义为:
如果一个数是正数,则编码为这个数的本身;
如果一个数是负数,则编码为其补码,即9999-|x|。
举个例子,如32767,其编码为 0003 2767; -4251,其编码为5738
加法是很好实现的,我们在此用微易码补码,就是要实现减法,因为减法要借位,在编程上是不容易实现的。
我们通过几个例子来看微易码补码的使用。
先举几个没有进位的例子。

所谓逻辑进位,就是两个数最后一位万进制相加,若大于10000,则进位为1,否则为0。在此有一个规则:除了两个正数相加以外,其他情况若逻辑进位即最后一位相加后进位为1,则最后结果要加1。除此之外,两个数相加之后的和的符号也需要通过异或运算判断,即 ^ ,规则是和的符号是: (第一个数的符号) 异或 (第二个数的符号) 异或 (逻辑进位)


可以看到,有无进位是不一样的,所以为了方便编程,我们需要给每个运算数编码的时候都多加一位万进制,若是正数,则在前面加0000,若是负数,则在前面加9999。
以上即为微易码补码的定义即运算规则。
Ⅹ 将数据编码 及 解码
编码和解码都是比较简单,没有复杂的逻辑,只需要根据分析将其变成编码即可,代码如下:
void mecComplement(HUGE_NUMBER *firstHugeNumber, HUGE_NUMBER *secondHugeNumber,
HUGE_NUMBER *firstComplement, HUGE_NUMBER *secondComplement) {
int i;
int j;
int figure;
int firstSorceCount = firstHugeNumber->count;
int secondSorceCount = secondHugeNumber->count;
int firstSroceFigure = (firstSorceCount + 3) / 4;
int secondSorceFigure = (secondSorceCount + 3) / 4;
if (firstSorceCount >= secondSorceCount) {
firstComplement->count = secondComplement->count = firstSorceCount + 4;
} else {
firstComplement->count = secondComplement->count = secondSorceCount + 4;
}
figure = (firstComplement->count + 3) / 4;
firstComplement->sign = firstHugeNumber->sign;
secondComplement->sign = secondHugeNumber->sign;
firstComplement->number = (int *) calloc(sizeof(int), figure);
secondComplement->number = (int *) calloc(sizeof(int), figure);
if (0 == firstComplement->sign) {
for (i = 0; i < figure - firstSroceFigure; i++) {
firstComplement->number[i] = 0;
}
for (i = figure - firstSroceFigure, j = 0; j < firstSroceFigure; i++, j++) {
firstComplement->number[i] = firstHugeNumber->number[j];
}
} else {
for (i = 0; i < figure - firstSroceFigure; i++) {
firstComplement->number[i] = 9999;
}
for (i = figure - firstSroceFigure, j = 0; j < firstSroceFigure; i++, j++) {
firstComplement->number[i] = 9999 - firstHugeNumber->number[j];
}
}
if (0 == secondComplement->sign) {
for (i = 0; i < figure - secondSorceFigure; i++) {
secondComplement->number[i] = 0;
}
for (i = figure - secondSorceFigure, j = 0; j < secondSorceFigure; i++, j++) {
secondComplement->number[i] = secondHugeNumber->number[j];
}
} else {
for (i = 0; i < figure - secondSorceFigure; i++) {
secondComplement->number[i] = 9999;
}
for (i = figure - secondSorceFigure, j = 0; j < secondSorceFigure; i++, j++) {
secondComplement->number[i] = 9999 - secondHugeNumber->number[j];
}
}
reverse(firstComplement);
reverse(secondComplement);
}
同样,根据解码规则,也可以轻松完成解码部分,在此不再赘述。代码如下:
void decode(HUGE_NUMBER *result) {
int i;
int figure = (result->count + 3) / 4;
if (1 == result->sign) {
for (i = 0; i < figure; i++) {
result->number[i] = 9999 - result->number[i];
}
}
reverse(result);
}
ⅩⅠ *** 微易码补码实现加法和减法
完成了种种准备,终于可以开始写运算的函数了。
我们先手工过程,总结自己做加法的过程。其实这个过程是很容易对应到程序中的,在此注意的是我们的进位,到10000进1。
对应例子 32767 + 4251 = 37018。 将两个数初始化并且倒置后,得到 2767 3 和 4251,先将两个低位相加,即2767 + 4251,得到7018,此时7018 / 10000 = 0,即进位carry为0,7018 % 10000 = 7018,此时退位abdicate = 7018, 所以我们在结果的第一位保存7018。接下来再计算3 + 0 + carry = 3,则在第二位保存3,此时变完成了加法。我们只需要将这个简单的过程写出来就完成了。代码如下:
void plusAndMinus(HUGE_NUMBER *firstHugeNumber, HUGE_NUMBER *secondHugeNumber, HUGE_NUMBER *result) {
int i;
int temp;
int figure;
int abdicate;
int tempCarry;
int carry = 0;
int pointFigure = 0;
HUGE_NUMBER firstComplement;
HUGE_NUMBER secondComplement;
mecComplement(firstHugeNumber, secondHugeNumber,
&firstComplement, &secondComplement);
figure = (firstComplement.count + 3) / 4;
result->number = (int *) calloc(sizeof(int), figure);
for (i = 0; i < figure; i++) {
temp = firstComplement.number[i] + secondComplement.number[i] + carry;
abdicate = temp % 10000;
carry = temp / 10000;
result->number[i] = abdicate;
}
tempCarry = carry;
if (1 == firstComplement.sign || 1 == secondComplement.sign) {
for (i = 0; i < figure; i++) {
temp = result->number[i] + tempCarry;
abdicate = temp % 10000;
tempCarry = temp / 10000;
result->number[i] = abdicate;
}
}
result->sign = firstComplement.sign ^ secondComplement.sign ^ carry;
for (i = figure; 0 == result->number[i - 1] || 9999 == result->number[i - 1]; i--) {
pointFigure++;
}
result->count = (figure - pointFigure) * 4 - 3;
decode(result);
destory(&firstComplement);
destory(&secondComplement);
}
有几行代码需要注意
result->sign = firstComplement.sign ^ secondComplement.sign ^ carry;
for (i = figure; 0 == result->number[i - 1] || 9999 == result->number[i - 1]; i--) {
pointFigure++;
}
result->count = (figure - pointFigure) * 4 - 3;
因为输出函数是需要根据count数来决定的,因为我们之前将数字转成编码的时候,为了防止进位,是多加了一位的,即如果就这样输出最后会输出00022565诸如此类的数字,所以在输出前我们需要找到无效数字的位数,并通过改变count的数量,不将其输出。
ⅩⅡ *** 用多项式思想实现乘法
乘法如果想通了,其实是比加法要容易的。它的逻辑更加简单。我举一个例子,32767 * 4251 = 139 292 517
还是先将两个数初始化并倒置,得到2767 3,和4251,根据数学推演,可以化成
32767 * 4251 = 2767 * 4251 + 30000 * 4251。从这里我们发现,其实这个式子可以变成
(2767 * 10000 ^ 0 )* (4251 * 10000 ^ 0) + (3 * 10000 ^ 1) * (4251 * 10000 ^ 0)
一万的几次方实际上就是它们的下标。所以如果把一万的次方看成是一个未知量,乘法实际上就相当于多项式的乘法。
比如(3x + 4y + 3z)*(2x + 3y) = 6x^2 + 9xy + 8xy + 12y^2 + 6xz + 9yz 。
其中x,y,z就相当于10000的0,1,2次方,与其下标对应。并且,如果未知量如果相同,还可以两两合并。
按照这个思路,我们就可以开始编程了。其进制还是和加法一样,对应位相乘后还是要考虑进位和退位问题。代码如下:
void multiply(HUGE_NUMBER *firstHugeNumber, HUGE_NUMBER *secondHugeNumber, HUGE_NUMBER *accumulate) {
int i;
int j;
int temp;
int abdicate;
int carry = 0;
int firstSorceCount = firstHugeNumber->count;
int secondSorceCount = secondHugeNumber->count;
int accumulateCount = firstSorceCount + secondSorceCount;
int firstSroceFigure = (firstSorceCount + 3) / 4;
int secondSorceFigure = (secondSorceCount + 3) / 4;
int accumulateFigure = (accumulateCount + 3) / 4;
accumulate->sign = firstHugeNumber->sign ^ secondHugeNumber->sign;
accumulate->number = (int *) calloc(sizeof(int), accumulateFigure);
accumulate->count = accumulateCount;
reverse(firstHugeNumber);
reverse(secondHugeNumber);
for (i = 0; i < firstSroceFigure; i++) {
for (j = 0; j < secondSorceFigure; j++) {
temp = firstHugeNumber->number[i] * secondHugeNumber->number[j] + accumulate->number[i+j];
abdicate = temp % 10000;
carry = temp / 10000;
accumulate->number[i+j] = abdicate;
accumulate->number[i+j+1] += carry;
}
}
reverse(accumulate);
}
需要注意的是,由于x,y相当于下标,所以一定要注意对应,将下标为i的位数和下标为j的位数对应的乘积放入下标为[i + j]的积的数组中。
ⅩⅢ 完整代码
完整代码如下:
#include 运行结果如下:
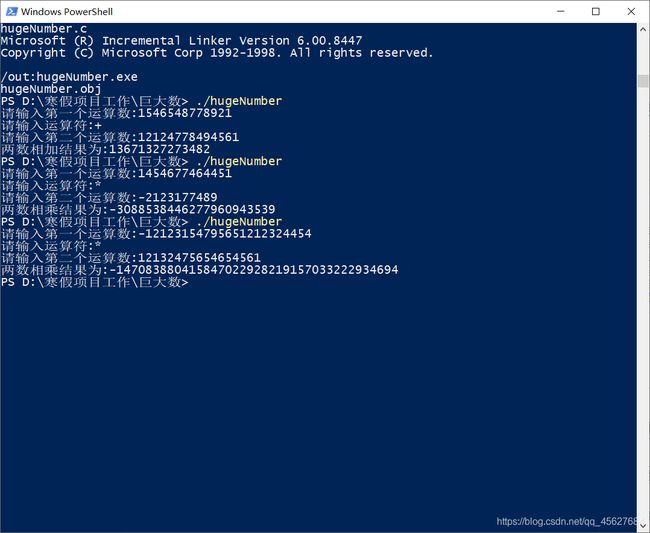
再次声明,boolean的实质类型为unsigned char。
以上即为巨大数的分析即实现,感谢朱洪先生的指导。