【数据结构与算法】-＞算法-＞贪心算法

Ⅰ 前言

贪心算法（Greed Algorithm）的思想其实是生活中一个很常用的思想，贪心算法本身也有很多经典的应用，比如哈夫曼编码（Huffman Coding）、Prim 和 Kruskal 最小生成树算法、Dijkstra 单源最短路径算法。最小生成树和最短路径在我后面的文章中会介绍，哈夫曼编码在我之前的文章中也讲过了，今天我们再从贪心算法的角度来看看。

【数据结构与算法】-＞数据结构-＞哈夫曼树-＞哈夫曼编码&解码

Ⅱ 贪心算法的理解

关于贪心算法，我们先看一个例子。

假设我们有个可以容纳 100kg 物品的背包，可以装各种物品。我们有以下 5 种豆子，每种豆子的总量和总价值都各不相同，为了让背包中所装物品的价值最大，我们要如何选择在背包中装哪些豆子，每种豆子又该装多少呢？

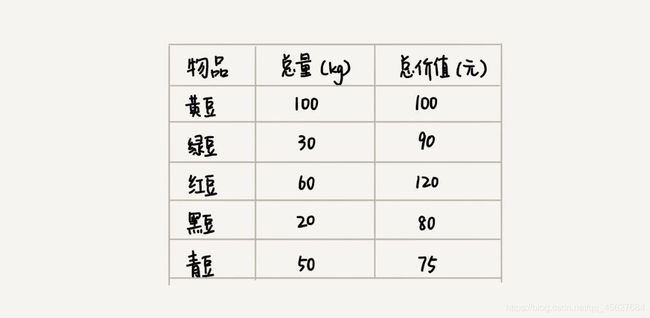
实际上，这个问题不是很复杂，我们只要先计算一下每个物品的单价，按照单价由高到低来排序，然后就按这个顺序装就好了。单价从高到低排列为：黑豆、绿豆、红豆、青豆、黄豆。所以，我们可以往背包里装 20kg 黑豆，30kg 绿豆，50kg 红豆。

这个问题解决思路还是比较容易想到的，它本质借助的就是贪心算法。结合这个例子，我总结一下贪心算法解决问题的步骤。

第一步，当我们看到这类问题的时候，首先要联想到贪心算法：针对一组数据，我们定义了限制值和期望值，希望从中选出几个数据，在满足限制值的情况下，期望值最大。

对应到我们举的例子中，限制值就是重量不能超过 100kg，期望值就是物品的总价值。这组数据就是 5 种豆子，我们从中选出一部分，满足重量不超过 100kg，并且总价值最大。

第二步，我们尝试看下这个问题是否可以用贪心算法解决：每次选择当前情况下，在对限制值同等贡献量的情况下，对期望值贡献最大的数据。

对应刚才的例子，我们每次都从剩下的豆子里面，选择单价最高的，也就是重量相同的情况下，对价值贡献最大的豆子。

第三步，我们举几个例子看贪心算法产生的结果是否是最优的。大部分情况下，举几个例子验证一下就可以了。严格地证明贪心算法的正确性，是非常复杂的，需要涉及比较多的数学推理。而且，从实践的角度来说，大部分能用贪心算法解决的问题，贪心算法的正确性都是显而易见的，也不需要严格的数学推导证明。

实际上，用贪心算法解决问题的思路，并不总能给出最优解。我举一个例子。

在一个有权图中，我们从顶点 S 开始，找一条到顶点 T 的最短路径（路径中边的权值和最小）。贪心算法的解决思路是，每次都选择一条跟当前顶点相连的权最小的边，直到找到顶点 T。按照这种思路，我们求出的最短路径是 S->A->E->T，路径长度是 1 + 4 + 4 = 9。

但是，这种贪心的选择方式，最终求的路径并不是最短路径，因为路径 S->B->D->T 才是最短路径，因为这条路径的长度是 2 + 2 + 2 = 6。那为什么在这个问题上贪心算法不工作了呢？

原因就是，前面的选择，会影响后面的选择，如果我们第一步从顶点 S 走到顶点 A，那接下来面对的顶点和边，跟第一步从顶点 S 走到顶点 B，是完全不同的。所以，即便我们第一步选择最优的走法（边最短），但有可能因为这一步选择，导致后面每一步的选择都很糟糕，最终也无缘最优解了。

Ⅲ 贪心算法实战分析

对于贪心算法，你可能还是很懵。如果死抠理论的话，确实很难透彻理解。掌握贪心算法的关键就是多练习。那么，我们就来分析几个具体的例子，帮助你更深地理解贪心算法。

1. 分糖果

我们有 m 个糖果和 n 个孩子。我们现在要把糖果分给这些孩子，但是糖果少，孩子多（m < n），所以糖果只能分配给一部分孩子。

每个糖果的大小不等，这 m 个糖果的大小分别是 s1，s2，s3，……，sm。除此之外，每个孩子对糖果大小的需求也是不一样的，只有糖果的大小对糖果的需求也是不一样的，只有糖果的大小大于等于孩子对糖果大小的需求的时候，孩子才得到满足。假设这 n 个孩子对糖果大小的需求分别是 g1，g2，g3，……，gn。

那么，要怎么分配糖果，能尽可能满足最多数量的孩子？

我们可以把这个问题抽象成，从 n 个孩子中，抽取一部分孩子分配糖果，让满足的孩子的个数（期望值）是最大的。这个问题的限制值就是糖果个数 m。

我们现在来看看如何用贪心算法来解决。对于一个孩子来说，如果小的糖果可以满足，我们就没必要用更大的糖果，这样更大的就可以留给其他对糖果大小需求更大的孩子。另一方面，对糖果大小需求小的孩子更容易被满足，所以，我们可以从需求小的孩子开始分配糖果，因为满足一个需求大的孩子和满足一个需求小的孩子，对我们的期望值的贡献都是一样的。

我们从每次剩下的孩子中，找出对糖果大小需求量最小的，然后发给他剩下的糖果中能满足他的最小的糖果，这样得到的分配方案，也就是满足的孩子个数最多的方案。

2. 钱币找零

这个问题在我们的日常生活中更加普遍，假设我们有 1 元，2 元，5 元，10 元，20 元，50 元，100 元这些面额的纸币，它们的张数分别是 c1, c2, c5, c10, c50, c100。我们现在要用这些钱来支付 K 元，最少要用多少张纸币呢？

在生活中，我们肯定是先用面值最大的来支付，如果不够，就继续用更小一点面值的，以此类推，最后剩下的用 1 元来补齐。

在贡献值相同期望值（纸币数目）的情况下，我们希望多贡献点金额，这样就可以让纸币数更少，这就是一种贪心算法的解决思路。

3. 区间覆盖

假设我们有 n 个区间，区间的起始端点和结束端点分别是 [l1, r1]， [l2, r2]， [l3, r3]，…， [ln, rn]。我们从这 n 个区间中选出一部分区间，这部分区间满足两两不相交（端点相交的情况不算相交），最多能选出多少个区间呢？

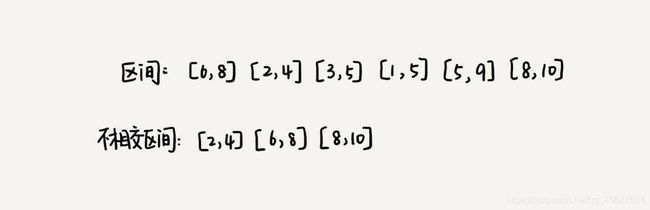
这个问题的处理思路稍微不是那么好懂，但是这个处理思路在很多贪心算法问题中都有用到，比如任务调度、教师排课等等问题，所以还是挺重要的，希望大家能理解。

这个问题的解决思路是这样的：我们假设这 n 个区间中最左端点是 lmin，最右端点是 rmax。这个问题就在于，我们选择几个不相交的区间，从左到右将 [lmin, rmax] 覆盖上。我们按照起始端点从小到大的顺序对这 n 个区间排序。

我们每次选择的时候，左端点跟前面的已经覆盖的区间不重合，右端点尽量小的，这样就可以让剩下的未覆盖区间尽可能的大，就可以放置更多的区间。这实际上就是一种贪心的选择方法。

Ⅳ 生活中的贪心算法

我们上面提到了哈夫曼编码，其实在我的下面这篇文章中，已经把哈夫曼编码讲得很详细了，我不再赘述。

【数据结构与算法】-＞数据结构-＞哈夫曼树-＞哈夫曼编码&解码

事实上哈夫曼编码，还有著名的莫尔斯密码，都是贪心算法的体现，它们都是希望能将出现频度最高的字符用最短的编码替代，可以节省很多空间。

我们看日常生活，无论是国家的宏观决策，还是金融市场上的投资理论，其实都体现了贪心算法的思想，在资源一定的情况下，达到最优配置，使得社会福祉最大化。经济学中著名的科斯定理，帕累托改进，本质上都是这个道理，有限值，有期望，然后进行资源配置。

我们写程序，一定不要局限在一个点上，要看到生活，看到实际，时不时将自己跳脱出来，才能有一个更全面和清晰的视角。这是我的一点额外的小看法。

关于哈夫曼编码，我还实现了一个不小的小项目，其实就是哈夫曼编码的实际应用，我写出了一个切实可以压缩文件的程序，压缩率也在 70% 到 80%之间，大家有兴趣可以看看。

【C语言-＞数据结构与算法】-＞哈夫曼压缩&解压缩-＞第一阶段-＞哈夫曼编码&解码的实现

【C语言->数据结构与算法】->哈夫曼压缩&解压缩->终局->如何做一个自己独有的压缩软件

另，本文的内容主要来源于极客时间王争的《数据结构与算法之美》。