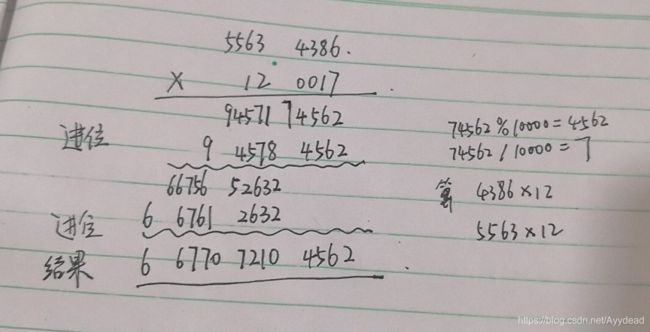巨大数的实现
巨大数的实现
-
- 一、巨大数
-
- 1.基本概念
- 2.计算机中巨大数
- 二、万进制
-
- 1.基本概念
- 2.万进制的优势
- 三、巨大数录入与输出
-
- 1.录入
- 2.输出
- 四、巨大数加减法--微易码补码实现法
-
- 1.微易码补码：
- 2.加法E
- 3.减法
- 五、巨大数的乘法（除法暂时没写）
-
- 1.乘法
- 除法暂时没有，没写出想要的感觉。
- 六、总结
锲子：还记得第一次面对星空浩瀚的震撼吗？还记得一颗颗数星星吗？那么星星到底有多少颗呢？
可惜我们从来没有数清过，只知道星星好多，好多，好美。
其实，肉眼可以观察到的星星接近7000颗，而且根据亮度分为1到6等。
当然，星空的浩瀚自然不只这么点。宇宙中大约有7乘10的22次方颗星星。 这是个多大的数字？全球人的手指头和脚指头加起来都不够数。符合人们心里的无限大。
可惜，我不太喜欢定义模糊的数字，所以我想用计算机存储起来。
一、巨大数
1.基本概念
抱歉，我没有百度到。╥﹏╥。说一下个人理解吧。
本质是数，1也可以称之为巨大数，不过巨大数的更指大于千亿（小学只学到千亿( • ̀ω•́ )✧）的数吧。
巨大数要满足有效精确位数起码达到百位。
2.计算机中巨大数
C语言中，常用int 类型只能表示-2147483648~2147483648（2的31次方）。其数据范围在正负21亿内。但是远远不够，而比它范围大的double类型，其有效精确位数只有15位。不满足我们想要实现具体的百位数，千位数。所以尝试用其他方式来表示巨大数。具体得做到，存储巨大数，输出巨大数，实现巨大数的四则运算
简单思路：
存储巨大数： 数组。（一个数字一个位）
输出巨大数： 字符串 形式输出。
实现运算： 加减可以同位加减，但要注意进位和借位。乘法就有点麻烦了。
上述想法挺好的，也便于理解。尤其是存储和输出特别轻松。有因必有果。运算上就出现速度过慢。
那么，还有更好的想法？有的٩(๑❛ᴗ❛๑)۶。
进阶思路：使用万进制。 一个下标，对应着一个0~9999的数。
二、万进制
曾有老师笑称，人有10个手指，所以10进制早于2进制出现。如果我们更习惯2进制，那么计算机发展应该更加快。那如果我们最早使用万进制呢？世界会是咋样？哈哈，估计10000元只相当于现在1元的购买力！(～￣▽￣)～
1.基本概念
简单来说，就是10进制中的时变成了10000。以前0~ 9中，满10进一位，如今，0~9999中满一万进一位。
2.万进制的优势
1）计算速度加快。10111 2222 时，10进制需要相加4次，万进制只加一次。
2）能保护数据。 10000 * 10000最大是1亿，int可以存储。而使用10万进制时，相乘最大是100亿，int无法保护其准确性。
思路已经有了，需要实现了。
万进制存储地方：
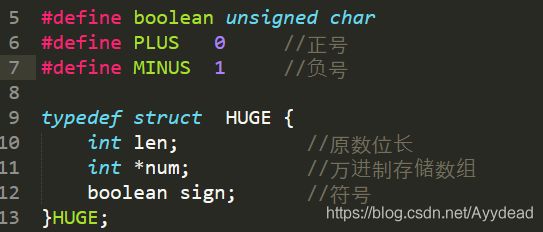
三、巨大数录入与输出
1.录入
基本步骤：
1.得到用户键盘输入的巨大数。
2.获得位长，数的正负。
3.给巨大数分组，4个为一组，不足4个时视为一组。
PS:不足4个的为一组时，是最大位的数。
// 解决符号问题
void dealSign(HUGE *hn, char *num) {
int ch = num[0];
if (ch == '-') {
hn->sign = MINUS;
}else if (ch == ' ' ) {
hn->sign = PLUS;
hn->len -= 1; //减去正号长度
}else if(ch >= '0' && ch <= '9') {
hn->sign = PLUS;
}else {
printf("errror!!!\n");
}
hn->len -= hn->sign; // 减去可能存在的符号位的影响
}
//录入巨大数
void getHugeNum(HUGE *hn) {
char num[128] = {
0}; //储存输入的字符串
char a[5] = {
0}; //摘取4个长度的字符串
int start; //用来将跳过符号位
int j;
int hnIndex = 0; //万进制储存数的下标
gets(num);
hn->len = strlen(num); //字符串长度
j = hn->len;
//解决符号
dealSign(hn, num);
hn->num = (int *)malloc(sizeof(int)* ((hn->len 3) / 4 1));
start = hn->len < j ? 1 : 0;
hnIndex = (hn->len 3) / 4 - 1;
if (hn->len % 4 != 0) {
//处理不足4个的情况。
strncpy(a, num start, hn->len % 4);
hn->num[hnIndex] = atoi(a);
hnIndex--;
}
//处理满足4个的情况。
for (j = start hn->len % 4; hnIndex >= 0 && j <= hn->len start; j = 4, hnIndex--) {
strncpy(a, num j, 4);
hn->num[hnIndex] = atoi(a);
}
}
注意： 1. strncpy（）， atoi（）函数的使用。
2.可以在判断正负后删去正负号，无需一定和我一样操作。
2.输出
基本思路：
1.判断是否输出正负号。
2.解决最大位前不能多输出0，中间位不能少输出0.
例如： 25226000025
要输出为 252 2600 0025
3. 0输出时不要有正负。
void showHugeNum(HUGE *hn) {
int bigIndex =(hn->len 3) / 4 - 1; //最大位数下标，解释1如下
if (hn->num[0] == 0 && hn->num[bigIndex] == 0) {
printf("0\n");
return;
}
if (hn->sign == MINUS) {
printf("%c", '-');
}
printf("%d ", hn->num[bigIndex]);
bigIndex--;
for (; bigIndex >= 0; bigIndex--) {
printf("d ", hn->num[bigIndex]);
}
printf("\n");
}
解释1： 如何通过巨大数位长来确定万位制存储长度。
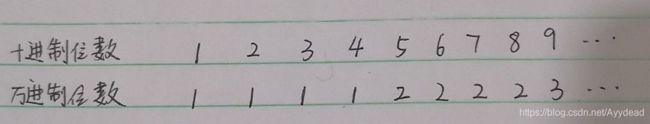十进制位数除以4不行，5 / 4 为1，用 5 / 4 1时，4 / 4 1 不符合。 而 （5 3） /4 和 （4 3）/ 4 都满足。
四、巨大数加减法–微易码补码实现法
想必大家都明白加减法很类似。但是我们手工过程中，加法必须考虑进位一事，减法必须考虑借位一事。很是麻烦。那么大家还记得计算机是如何实现加减的吗？
接下来，隆重介绍微易码补码。
1.微易码补码：
正数的“微易码”补码是 **原数**
如 2238 0015 （原码） 2238 0015 （微易码补码）
负数的“微易码”补码是 **同位长的最大数减去原数**
如 - 2238 0015 （原码）
微易码补码为 9999 9999 - 2238 0015 = 7761 9984
记住符号不变。
由于个人数学不够好，对于微易码补码的证明不能给出逻辑推理。只能在自己的有关微易码补码文章里，举例说明。也怕文章中过长。链接如下：暂无
不过， 我会说下原则：
2.加法E
具体实现如下：
基本步骤：
1.原数转化为微易码补码形式。
2.按上述原则实现相加。
3.将补码形式转变回来。
void add(HUGE *hn1, HUGE *hn2, HUGE *result) {
int i;
int a, b;
int temp;
boolean carry = 0;
a = (hn1->sign == MINUS) ? 9999 : 0;
b = (hn2->sign == MINUS) ? 9999 : 0;
for (i = 0; i <= (result->len 3) / 4; i ) {
temp = i <= ((hn1->len 3) / 4) ? hn1->num[i] : a;
temp = i <= ((hn2->len 3) / 4) ? hn2->num[i] : b;
temp = carry;
carry = temp >= 10000 ? 1 : 0;
result->num[i] = temp % 10000;
}
result->num[0] = carry;
for (i = 0; result->num[i] > 9999 && i <= (result->len 3) / 4; i ) {
result->num[i] %= 10000;
result->num[i 1] ;
}
result->sign = hn1->sign ^ hn2->sign ^ carry;
if (result->sign == MINUS) {
for (i = 0; i <= (result->len 3) / 4; i ) {
result->num[i] = 9999 - result->num[i];
}
}
if ((result->len 3) / 4 > 0 && result->num[(result->len 3) / 4] != 0) {
result->len = 1;
}
}
void resumeHugeNum(HUGE *hn) {
int i;
if (hn->sign == MINUS) {
for (i = 0; i <= (hn->len 3) / 4; i ) {
hn->num[i] = 9999 - hn->num[i];
}
}
}
void changeHugeNum(HUGE *hn) {
int i;
hn->num[(hn->len 3) / 4] = (hn->sign == MINUS) ? 9999 : 0;
if (hn->sign == MINUS) {
for (i = 0; i < (hn->len 3) / 4; i ) {
hn->num[i] = 9999 - hn->num[i];
}
}
}
void addHugeNum(HUGE *hn1, HUGE *hn2) {
HUGE result = {
0, {
0}, PLUS,
};
result.len = hn1->len < hn2->len ? hn2->len : hn1->len;
result.num = (int *)malloc(sizeof(int) * (result.len 3) / 4 1);
changeHugeNum(hn1);//转变为补码
changeHugeNum(hn2);
add(hn1, hn2, &result);//实现相加
showHugeNum(&result);
resumeHugeNum(hn1);//补码恢复为原数
resumeHugeNum(hn2);
free(result.num);
}
3.减法
加法解决了，减法简单。5-3 = 5 （-3），所以调用函数。
void subHugeNum(HUGE *hn1, HUGE *hn2) {
hn2->sign = (hn2->sign == MINUS) ? PLUS : MINUS;// 修改第二个数符号
addHugeNum(hn1, hn2);
hn2->sign = (hn2->sign == MINUS) ? PLUS : MINUS;//恢复第二个数符号
}
五、巨大数的乘法（除法暂时没写）
1.乘法
思路很简单，就跟10进制的乘法一样。步骤如下：
代码如下：
void multiplyHugeNum(HUGE *hn1, HUGE *hn2) {
HUGE result = {
0, {
0}, PLUS,
};
int i, j;
int temp;
result.len = hn1->len hn2->len;
result.num = (int *)calloc(sizeof(int) , (result.len 3) / 4);
result.sign = (hn1->sign == hn2->sign) ? PLUS : MINUS;
for (i = 0; i < (hn2->len 3) / 4; i ) {
for (j = 0; j < (hn1->len 3) / 4; j ) {
temp = hn2->num[i];
temp *= hn1->num[j];
temp = result.num[i j];
result.num[i j] = temp % 10000;
result.num[i j 1] = temp / 10000;
}
}
//解决结果位长
if (result.len % 4 == 0 && result.num[(result.len 3) / 4 - 1] < 1000 ) {
result.len--;
}else if (result.len % 4 == 3 && result.num[(result.len 3) / 4 - 1] < 100 ) {
result.len--;
}else if (result.len % 4 == 2 && result.num[(result.len 3) / 4 - 1] < 10 ) {
result.len--;
}else if (result.len % 4 == 1 && result.num[(result.len 3) / 4 - 1] < 1 ) {
result.len--;
}
showHugeNum(&result);
}
除法暂时没有，没写出想要的感觉。
最后主函数和函数名在这：就不在完整贴出了，我已经贴上了所有子函数。
#include
#include
#include
void getHugeNum(HUGE *hn);
void dealSign(HUGE *hn, char *num);
void showHugeNum(HUGE *hn);
void addHugeNum(HUGE *hn1, HUGE *hn2);
void changeHugeNum(HUGE *hn);
void subHugeNum(HUGE *hn1, HUGE *hn2);
void resumeHugeNum(HUGE *hn);
void add(HUGE *hn1, HUGE *hn2, HUGE *result);
void multiplyHugeNum(HUGE *hn1, HUGE *hn2);
int main() {
HUGE hn1 = {
0, {
0}, PLUS,
};
HUGE hn2 = {
0, {
0}, PLUS,
};
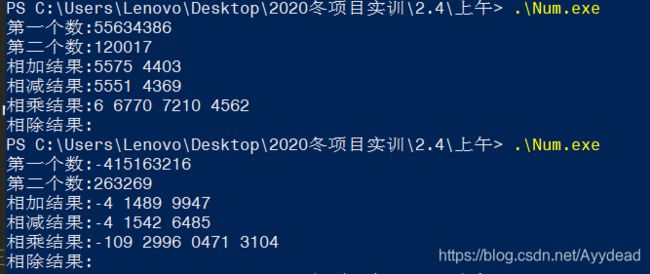
printf("第一个数:");
getHugeNum(&hn1);
printf("第二个数:");
getHugeNum(&hn2);
printf("相加结果:");
addHugeNum(&hn1, &hn2);
printf("相减结果:");
subHugeNum(&hn1, &hn2);
printf("相乘结果:");
multiplyHugeNum(&hn1, &hn2);
free(hn1.num);
free(hn2.num);
return 0;
}
实现：
六、总结
1.自己动手时，将自己的思路转化成一行行代码时，实现行动跟上了思想。切记眼高手低。
2.最大的感触是思考。思考的越深，别人的想法你能很快想出漏洞，因为你考虑到了。同时越思考，自己的逻辑严密更强。举个例子，这次我花了不少时间修改一些代码，看似不影响多少，但是他的完整性就不好，鲁棒性弱。整体思路都会，但细节上总是缺一点。 切记，多思考。
3.小黄鸭调试。出现错误，自己给小黄鸭讲一讲每行代码的意义。慢慢就发现了自己错诶。
感谢指导老师：铁血教主
笔者水平有限，目前只能描述以上问题，如果有其他情况，可以留言，有错误，请指教，有继续优化的，请分享，谢谢！
2020年02.05 家