模式串匹配之KMP算法&BM算法&sunday算法

本文部分内容出自https://blog.csdn.net/v_JULY_v/article/details/7041827

字符串匹配的问题：有一个长度为n的文本串S，和一个长度为m的模式串P，现在要查找P在S中的位置。

这个问题的暴力解法时间复杂度高达o(nm)

能不能更高效的解决这个匹配问题呢？

KMP算法

这个算法取消了暴力算法中的文本串指针i的回溯，每次失配时只回溯模式串的指针j，极大提高了效率

每次失配时，i无需改变；令j=next[j]，等价于把模式串向右移动了j-next[j]位继续匹配

若文本串s的长度为n 模式串p的长度为m

那么计算next数组的时间是o(m) 匹配的时间是o(n)

因此kmp算法时间总体时间复杂度为o(m+n)

//
// Created by DongChenglong on 2020/5/13.
//

#include 
#include 

using namespace std;

//next[i]的含义为 若i位置处失配 那么模式串指针应该回溯到next[i]
void getnext(int next[], string s) {
     
    int j = 0, k = -1;
    next[0] = -1;

    while (j < s.length()-1 ) {
     
        //循环小于len-1是因为 next[i]的意义是代表了前i-1个字符的最大相同前缀后缀 因此next[len-1]的值只需要比较到0～len-2这个区间
        if (k == -1 || s[j] == s[k]) {
      //k==-1表示 已经对比到了最前面 相同的后缀前缀长度为0
            j++;
            k++;
            if (s[j] != s[k])  
                next[j] = k;
            else  //这是一处优化 考虑abab 如果后一个b失配 那么若回溯到了第一个b 也必定失配 是一次无意义的比较
                next[j] = next[k];
        }
        else
            k = next[k];
    }
}

int KMP(string s, string t) {
     
    int n = s.length();
    int m = t.length();
    int next[n+1];
    getnext(next, s);

//    for (int i = 0; i < n; ++i) printf("%d ", next[i]);
//    puts("");

    int i = 0, j = 0;
    while (i < n && j < m) {
     
        if (i == -1 || s[i] == t[j]) {
     
            ++i;
            ++j;
        } else i = next[i];
    }
    if (i >= n) return j - n;
    else return -1;
}

int main() {
     
	//返回模式串s 在主串中的下标
    string s = "bg", t = "ahbgdc";
    printf("%d\n", KMP(s, t));
}

next数组还可以用来找出模式串中的最小循环节

例如模式串ababab的最小循环节为ab

设有模式串为s 其长度为len

若len%(len-next[len])==0，则代表有循环节，且循环节长度为len-next[len]

//
// Created by DongChenglong on 2020/5/13.
//

#include 
#include 

using namespace std;

void getnext(int next[], string s) {
     
    int j = 0, k = -1;
    next[0] = -1;

    while (j < s.length()) {
     
        //循环小于len是因为找最小循环节需要计算到s[len]的值
        if (k == -1 || s[j] == s[k]) {
      //k==-1表示 已经对比到了最前面 相同的后缀前缀长度为0
            j++;
            k++;
            if (s[j] != s[k])  //考虑abab 如果后一个b失配 那么若回溯到了第一个b 也必定失配 一定是一次无意义的比较
                next[j] = k;
            else
                next[j] = next[k];
        } else
            k = next[k];
    }
}

int KMP(string s) {
     
    int n = s.length();
    int next[n + 1];
    getnext(next, s);

    for (int i = 0; i <= n; ++i) printf("%d ", next[i]);
    puts("");


    int c = s.length() - next[s.length()];
    if (s.length() % c == 0) {
     
        //有循环节 输出循环节长度
        return s.length() - next[s.length()];
    } else {
     
        //无循环节
        return -1;
    }
}

int main() {
     
    string s = "ababab";


    printf("%d\n", KMP(s));

}

BM算法

该算法从模式串的尾部开始匹配，且拥有在最坏情况下O(N)的时间复杂度。在实践中，比KMP算法的实际效能高。

BM算法定义了两个规则：

1 坏字符规则：当文本串中的某个字符跟模式串的某个字符不匹配时，我们称文本串中的这个失配字符为坏字符，此时模式串需要向右移动，移动的位数 = 坏字符在模式串中的位置 - 坏字符在模式串中最右出现的位置。此外，如果"坏字符"不包含在模式串之中，则最右出现位置为-1。

2 好后缀规则：当字符失配时，后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串上一次出现的位置，且如果好后缀在模式串中没有再次出现，则为-1。

下面举例说明BM算法。例如，给定文本串“HERE IS A SIMPLE EXAMPLE”，和模式串“EXAMPLE”，现要查找模式串是否在文本串中，如果存在，返回模式串在文本串中的位置。

1 首先，"文本串"与"模式串"头部对齐，从尾部开始比较。"S"与"E"不匹配。这时，“S"就被称为"坏字符”（bad character），即不匹配的字符，它对应着模式串的第6位。且"S"不包含在模式串"EXAMPLE"之中（相当于最右出现位置是-1），这意味着可以把模式串后移6-(-1)=7位，从而直接移到"S"的后一位。

2 依然从尾部开始比较，发现"P"与"E"不匹配，所以"P"是"坏字符"。但是，"P"包含在模式串"EXAMPLE"之中。因为“P”这个“坏字符”对应着模式串的第6位（从0开始编号），且在模式串中的最右出现位置为4，所以，将模式串后移6-4=2位，两个"P"对齐。

3 依次比较，得到 “MPLE”匹配，称为"好后缀"（good suffix），即所有尾部匹配的字符串。注意，“MPLE”、“PLE”、“LE”、"E"都是好后缀。

4 发现“I”与“A”不匹配：“I”是坏字符。如果是根据坏字符规则，此时模式串应该后移2-(-1)=3位。问题是，有没有更优的移法？

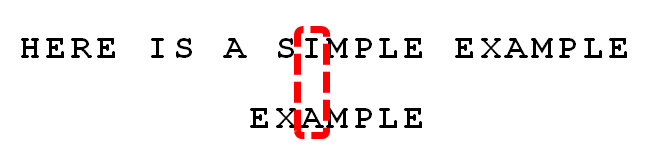
5 更优的移法是利用好后缀规则：当字符失配时，后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串中上一次出现的位置，且如果好后缀在模式串中没有再次出现，则为-1。
所有的“好后缀”（MPLE、PLE、LE、E）之中，只有“E”在“EXAMPLE”的头部出现，所以后移6-0=6位。
可以看出，“坏字符规则”只能移3位，“好后缀规则”可以移6位。每次后移这两个规则之中的较大值。这两个规则的移动位数，只与模式串有关，与原文本串无关。

6 继续从尾部开始比较，“P”与“E”不匹配，因此“P”是“坏字符”，根据“坏字符规则”，后移 6 - 4 = 2位。因为是最后一位就失配，尚未获得好后缀。

由上可知，BM算法不仅效率高，而且构思巧妙，容易理解。

Sunday算法

已经介绍了KMP算法和BM算法，这两个算法在最坏情况下均具有线性的查找时间。但实际上，KMP算法并不比最简单的c库函数strstr()快多少，而BM算法虽然通常比KMP算法快，但BM算法也还不是现有字符串查找算法中最快的算法，本文最后再介绍一种比BM算法更快的查找算法即Sunday算法。

Sunday算法由Daniel M.Sunday在1990年提出，它的思想跟BM算法很相似：

只不过Sunday算法是从前往后匹配，在匹配失败时关注的是文本串中参加匹配的最末位字符的下一位字符。
如果该字符没有在模式串中出现则直接跳过，即移动位数 = 匹配串长度 + 1；
否则，其移动位数 = 模式串中最右端的该字符到末尾的距离+1。
下面举个例子说明下Sunday算法。假定现在要在文本串"substring searching algorithm"中查找模式串"search"。

1 刚开始时，把模式串与文本串左边对齐：

substring searching algorithm
search
^

2 结果发现在第2个字符处发现不匹配，不匹配时关注文本串中参加匹配的最末位字符的下一位字符，即标粗的字符 i，因为模式串search中并不存在i，所以模式串直接跳过一大片，向右移动位数 = 匹配串长度 + 1 = 6 + 1 = 7，从 i 之后的那个字符（即字符n）开始下一步的匹配，如下图：

substring searching algorithm
　　　search
　　　^
　　　
3 结果第一个字符就不匹配，再看文本串中参加匹配的最末位字符的下一位字符，是’r’，它出现在模式串中的倒数第3位，于是把模式串向右移动3位（r 到模式串末尾的距离 + 1 = 2 + 1 =3），使两个’r’对齐，如下：
substring searching algorithm
　　　　 search
　　　　　　　^

4 匹配成功。

回顾整个过程，我们只移动了两次模式串就找到了匹配位置，缘于Sunday算法每一步的移动量都比较大，效率很高。

sunday算法c++实现：

//
// Created by DongChenglong on 2020/5/21.
//

#include 
#include 

using namespace std;


int sunday(string s, string t) {
     
    int lens = s.length();
    int lent = t.length();

    if (lens < lent) return -1;

    int index[26];
    for (int i = 0; i < 26; ++i) index[i] = -1;
    for (int i = 0; i < lent; ++i) {
     
        index[t[i] - 'a'] = i;
    }

    int i = 0;
    while (i < lens) {
     
        bool flag = true;
        for (int j = 0; j < lent; ++j) {
     
            if (s[i + j] == t[j]) continue;
            else {
     
                flag = false;
                if (i + lent < lens) {
     
                    if (s[i + lent] >= 'a' && s[i + lent] <= 'z') {
     
                        int pos = s[i + lent] - 'a';
                        if (index[pos] == -1) i += lent + 1;
                        else i = i + lent - index[pos];
                    } else i += lent + 1;
                    break;
                } else return -1;
            }
        }
        if (flag) return i;
    }
    return -1;
}

int main() {
     
    string s = "substring searching algorithm";
    string t = "search";

    printf("%d\n", sunday(s, t));
}