分治算法
分治算法
- 算法引入
- 主要思想
- 分治算法的步骤
- 分治算法适用的场景
- 伪代码
- 举个栗子
- 算法应用
-
-
- [169. 多数元素](https://leetcode-cn.com/problems/majority-element/)
- [53. 最大子序和](https://leetcode-cn.com/problems/maximum-subarray/)
- [50. Pow(x, n)](https://leetcode-cn.com/problems/powx-n/)
-
- 总结
算法引入
MapReduce（分治算法的应用） 是 Google 大数据处理的三驾马车之一，另外两个是 GFS 和 Bigtable。它在倒排索引、PageRank 计算、网页分析等搜索引擎相关的技术中都有大量的应用。
尽管开发一个 MapReduce 看起来很高深，感觉遥不可及。实际上，万变不离其宗，它的本质就是分治算法思想，分治算法。如何理解分治算法？为什么说 MapRedue 的本质就是分治算法呢？（关于mapreduce，我是在数据库里面了解过）
主要思想
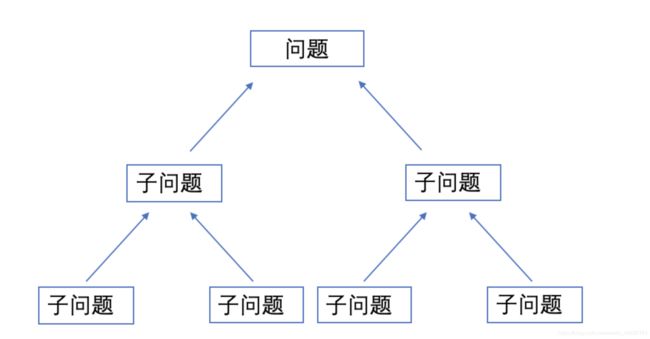
分治算法的主要思想是将原问题递归地分成若干个子问题，直到子问题满足边界条件，停止递归。将子问题逐个击破(一般是同种方法)，将已经解决的子问题合并，最后，算法会层层合并得到原问题的答案。
思想和二分差不多，时间复杂度差不多都是nlogn。
分治算法的步骤
- 分：递归地将问题分解为各个的子问题(性质相同的、相互独立的子问题)；
- 治：将这些规模更小的子问题逐个击破；
- 合：将已解决的子问题逐层合并，最终得出原问题的解；
分治算法适用的场景
- 原问题的计算复杂度随着问题的规模的增加而增加。
- 原问题能够被分解成更小的子问题。
- 子问题的结构和性质与原问题一样，并且相互独立，子问题之间不包含公共的子子问题。
- 原问题分解出的子问题的解可以合并为该问题的解。
伪代码
这里给出C++的伪代码：
void divide_conquer(problem, paraml, param2,...){
# 不断切分的终止条件
if problem is None:
print_result
return
# 准备数据
data=prepare_data(problem)
# 将大问题拆分为小问题
subproblems=split_problem(problem, data)
# 处理小问题，得到子结果
subresult1=self.divide_conquer(subproblems[0],p1,..…)
subresult2=self.divide_conquer(subproblems[1],p1,...)
subresult3=self.divide_conquer(subproblems[2],p1,.…)
# 对子结果进行合并 得到最终结果
result=process_result(subresult1, subresult2, subresult3,...)
}
举个栗子
通过应用举例分析理解分治算法的原理其实并不难，但是要想灵活应用并在编程中体现这种思想中却并不容易。所以，这里这里用分治算法应用在排序的时候的一个栗子，加深对分治算法的理解。
相关概念：
- 有序度：表示一组数据的有序程度
- 逆序度：表示一组数据的无序程度
一般通过计算有序对或者逆序对的个数，来表示数据的有序度或逆序度。
假设我们有 n 个数据，我们期望数据从小到大排列，那完全有序的数据的有序度就是 n ( n − 1 ) / 2 n(n-1)/2 n(n−1)/2，逆序度等于 0；相反，倒序排列的数据的有序度就是 0，逆序度是 n ( n − 1 ) / 2 n(n-1)/2 n(n−1)/2。
Q：如何编程求出一组数据的有序对个数或者逆序对个数呢？
因为有序对个数和逆序对个数的求解方式是类似的，所以这里可以只思考逆序对（常接触的）个数的求解方法。
方法1
- 拿数组里的每个数字跟它后面的数字比较，看有几个比它小的。
- 把比它小的数字个数记作 k，通过这样的方式，把每个数字都考察一遍之后，然后对每个数字对应的 k 值求和
- 最后得到的总和就是逆序对个数。
这样操作的时间复杂度是 O ( n 2 ) O(n^2) O(n2)（需要两层循环过滤）。那有没有更加高效的处理方法呢？这里尝试套用分治的思想来求数组 A 的逆序对个数。
方法2
- 首先将数组分成前后两半 A1 和 A2，分别计算 A1 和 A2 的逆序对个数 K1 和 K2
- 然后再计算 A1 与 A2 之间的逆序对个数 K3。那数组 A 的逆序对个数就等于 K1+K2+K3。
- 注意使用分治算法其中一个要求是，子问题合并的代价不能太大，否则就起不了降低时间复杂度的效果了。
如何快速计算出两个子问题 A1 与 A2 之间的逆序对个数呢？这里就要借助归并排序算法了。（这里先回顾一下归并排序思想）**如何借助归并排序算法来解决呢？归并排序中有一个非常关键的操作，就是将两个有序的小数组，合并成一个有序的数组。实际上，在这个合并的过程中，可以计算这两个小数组的逆序对个数了。每次合并操作，我们都计算逆序对个数，把这些计算出来的逆序对个数求和，就是这个数组的逆序对个数了。
算法应用
这里给出的题都是leetcode上面的题目，用C++完成的。
169. 多数元素
题目描述：
解题思路：
-
确定切分的终止条件
-
直到所有的子问题都是长度为 1 的数组，停止切分。
-
准备数据，将大问题切分为小问题
-
递归地将原数组二分为左区间与右区间，直到最终的数组只剩下一个元素，将其返回
-
处理子问题得到子结果，并合并
长度为 1 的子数组中唯一的数显然是众数，直接返回即可。
如果它们的众数相同，那么显然这一段区间的众数是它们相同的值。
如果他们的众数不同，比较两个众数在整个区间内出现的次数来决定该区间的众数
代码：
class Solution {
int count_range(vector<int>& nums,int target,int l,int h){
int count = 0;
for(int i=l;i<=h;i++){
if(nums[i]==target)
count++;
}
return count;
} #计算那个众数的个数
int majority_element(vector<int>& nums,int l,int h){
if(l==h){
return nums[l];
}
int mid=(l+h)/2;
int left_majority=majority_element(nums,l,mid);
int right_majority=majority_element(nums,mid+1,h);
if(count_range(nums,left_majority,l,h)>(h-l+1)/2){
return left_majority;
}
if(count_range(nums,right_majority,l,h)>(h-l+1)/2){
return right_majority;
}
return 0;
}
public:
int majorityElement(vector<int>& nums) {
return majority_element(nums, 0, nums.size() - 1);
}
};
这个题除了用分治外，还有暴力（可能会超时），哈希表，排序，随机化，Boyer-Moore 投票算法。感兴趣可以去看看解析。
53. 最大子序和
题目描述：
解题思路：
-
确定切分的终止条件
-
直到所有的子问题都是长度为 1 的数组，停止切分。
-
准备数据，将大问题切分为小问题
-
递归地将原数组二分为左区间与右区间，直到最终的数组只剩下一个元素，将其返回
-
处理子问题得到子结果，并合并
将数组切分为左右区间
对与左区间：从右到左计算左边的最大子序和 对与右区间：从左到右计算右边的最大子序和由于左右区间计算累加和的方向不一致，因此，左右区间直接合并相加之后就是整个区间的和
最终返回左区间的元素、右区间的元素、以及整个区间(相对子问题)和的最大值
代码：
class Solution {
public:
struct Status {
int lSum, rSum, mSum, iSum;
};
Status pushUp(Status l, Status r) {
int iSum = l.iSum + r.iSum;
int lSum = max(l.lSum, l.iSum + r.lSum);
int rSum = max(r.rSum, r.iSum + l.rSum);
int mSum = max(max(l.mSum, r.mSum), l.rSum + r.lSum);
return (Status) {
lSum, rSum, mSum, iSum};
};
Status get(vector<int> &a, int l, int r) {
if (l == r) return (Status) {
a[l], a[l], a[l], a[l]};
int m = (l + r) >> 1;
Status lSub = get(a, l, m);
Status rSub = get(a, m + 1, r);
return pushUp(lSub, rSub);
}
int maxSubArray(vector<int>& nums) {
return get(nums, 0, nums.size() - 1).mSum;
}
}; #这个代码是官网的那个代码，不过比较容易看懂，就不解释
同样这个题，也有动态规划，暴力，贪心可以求解；
我也用动态规划写过了
public int maxSubArray(int[] nums) {
int[] dp = new int[nums.length];
dp[0] = nums[0];
int max = nums[0];
for (int i = 1; i < nums.length; i++) {
dp[i] = Math.max(dp[i- 1] + nums[i], nums[i]);
if (max < dp[i]) {
max = dp[i];
}
}
return max;
}
50. Pow(x, n)
题目描述：
解题思路：
-
确定切分的终止条件
对n不断除以2，并更新n，直到为0，终止切分
-
准备数据，将大问题切分为小问题
对n不断除以2，更新
-
处理子问题得到子结果，并合并
x与自身相乘更新x
如果n%2 ==1
将p乘以x之后赋值给p(初始值为1)，返回p -
最终返回p
这里我不给出分治的代码，读者可以自己实现。
这里我给出一个比较简单的思路：使用折半计算，每次把n缩小一半，这样n最终会缩小到0，任何数的0次方都为1，这时候我们再往回乘，如果此时n是偶数，直接把上次递归得到的值算个平方返回即可，如果是奇数，则还需要乘上个x的值。还有一点需要引起我们的注意的是n有可能为负数，对于n是负数的情况，我们可以先用其绝对值计算出一个结果再取其倒数即可。我们让i初始化为n，然后看i是否是2的倍数，是的话x乘以自己，否则res乘以x，i每次循环缩小一半，直到为0停止循环。最后看n的正负，如果为负，返回其倒数。
就比如 ：求 23 ，就变成了2*22，24就成了42,再接着变化。
代码：
class Solution {
public:
double myPow(double x, int n) {
double sum = 1;
for(int i=abs(n);i!=0;i/=2){
if(i%2!=0){
sum*=x;
}
x*=x;
}
return n<0 ? 1/sum :sum;
}
};
总结
分治算法的思想，还是很常见的，虽然我这里的几个题基本上自己写都是用动态规划，快速幂，但是还是建议读者掌握。因为分而治之的思想，用在很多方面，不仅仅是编程上面，生活上也常见。