人工智障学习笔记——机器学习(7)FM/FFM

一.概念

FM(分解机模型)和FFM(基于域的分解机模型)是最近几年提出的模型，主要用于预估CTR/CVR，凭借其在数据量比较大并且特征稀疏的情况下，仍然能够得到优秀的性能和效果的特性，屡次在各大公司举办的CTR预估比赛中获得不错的战绩。

二.原理

FM（Factorization Machine）是由Konstanz大学Steffen Rendle（现任职于Google）于2010年最早提出的，旨在解决稀疏数据下的特征组合问题，相比SVM的二阶多项式核而言，FM在样本稀疏的情况下是有优势的；而且，FM的训练/预测复杂度是线性的，而二项多项式核SVM需要计算核矩阵，核矩阵复杂度就是N平方。

FFM（Field-aware Factorization Machine）最初的概念来自Yu-Chin Juan（阮毓钦，毕业于中国台湾大学，现在美国Criteo工作）与其比赛队员，是他们借鉴了来自Michael Jahrer的论文中的field概念提出了FM的升级版模型。通过引入field的概念，FFM把相同性质的特征归于同一个field
假设样本的 n 个特征属于 f 个field，那么FFM的二次项有 nf个隐向量。而在FM模型中，每一维特征的隐向量只有一个。FM可以看作FFM的特例，是把所有特征都归属到一个field时的FFM模型。根据FFM的field敏感特性，可以导出其模型方程。

其中，fj 是第 j 个特征所属的field。如果隐向量的长度为 k，那么FFM的二次参数有 nfk 个，远多于FM模型的 nk 个。此外，由于隐向量与field相关，FFM二次项并不能够化简，其预测复杂度是 O(kn2)O(kn2)。

详情参考   https://tech.meituan.com/deep-understanding-of-ffm-principles-and-practices.html

三.算法

算法代码：（源码见最后）

ffm_model ffm_train_on_disk(string tr_path, string va_path, ffm_parameter param) {

    problem_on_disk tr(tr_path);
    problem_on_disk va(va_path);

	ffm_model model = init_model(tr.meta.n, tr.meta.m, param);


	//cout << "ffm_train_on_disk:" << endl;
	
	//for (int i = 0; i < 10; i++)
	//{
	//	cout << "model.W[i]  "< prev_W(w_size, 0);
    if(auto_stop)
        prev_W.assign(w_size, 0);
    ffm_double best_va_loss = numeric_limits::max();

    cout.width(4);
    cout << "iter";
    cout.width(13);
    cout << "tr_logloss";
    if(!va_path.empty())
    {
        cout.width(13);
        cout << "va_logloss";
    }
    cout.width(13);
    cout << "tr_time";
    cout << endl;

    Timer timer;

    auto one_epoch = [&] (problem_on_disk &prob, bool do_update) {

        ffm_double loss = 0;
        vector outer_order(prob.meta.num_blocks);
        iota(outer_order.begin(), outer_order.end(), 0);
        random_shuffle(outer_order.begin(), outer_order.end());
        for(auto blk : outer_order) {
            ffm_int l = prob.load_block(blk);

            vector inner_order(l);
            iota(inner_order.begin(), inner_order.end(), 0);
            random_shuffle(inner_order.begin(), inner_order.end());

#if defined USEOMP
#pragma omp parallel for schedule(static) reduction(+: loss)
#endif
			
            for(ffm_int ii = 0; ii < l; ii++) {
                ffm_int i = inner_order[ii];

                ffm_float y = prob.Y[i];
                
                ffm_node *begin = &prob.X[prob.P[i]];

                ffm_node *end = &prob.X[prob.P[i+1]];

                ffm_float r = param.normalization? prob.R[i] : 1;

                ffm_double t = wTx(begin, end, r, model);

                ffm_double expnyt = exp(-y*t);

                loss += log1p(expnyt);
				//cout << ii <<"/"<< l <<" "<< i<<" " << y << " " << r ;
				//cout <<" " << t << " " << expnyt << endl;
				
                if(do_update) {
                   
                    ffm_float kappa = -y*expnyt/(1+expnyt);

                    wTx(begin, end, r, model, kappa, param.eta, param.lambda, true);
                }
            }
        }

        return loss / prob.meta.l;
    };

	//cout << "ffm_train_on_disk one_epoch" << endl;
    for(ffm_int iter = 1; iter <= param.nr_iters; iter++) {
        timer.tic();
        ffm_double tr_loss = one_epoch(tr, true);
        timer.toc();

        cout.width(4);
        cout << iter;
        cout.width(13);
        cout << fixed << setprecision(5) << tr_loss;

        if(!va.is_empty()) {
            ffm_double va_loss = one_epoch(va, false);

            cout.width(13);
            cout << fixed << setprecision(5) << va_loss;

            if(auto_stop) {
                if(va_loss > best_va_loss) {
                    memcpy(model.W, prev_W.data(), w_size*sizeof(ffm_float));                    
					cout.width(13);
					cout << fixed << setprecision(1) << timer.get() << endl;
					cout << endl << "Auto-stop. Use model at " << iter - 1 << "th iteration." << endl;
                    break;
                } else {
                    memcpy(prev_W.data(), model.W, w_size*sizeof(ffm_float));
                    best_va_loss = va_loss; 
                }
            }
        
		}
        cout.width(13);
        cout << fixed << setprecision(1) << timer.get() << endl;
    }

    return model;
}

其中wTx函数（非USESSE情况）：

inline ffm_float wTx(
    ffm_node *begin,
    ffm_node *end,
    ffm_float r,
    ffm_model &model, 
    ffm_float kappa=0, 
    ffm_float eta=0, 
    ffm_float lambda=0, 
    bool do_update=false) {

    ffm_int align0 = 2 * get_k_aligned(model.k);
    ffm_int align1 = model.m * align0;

    ffm_float t = 0;
    for(ffm_node *N1 = begin; N1 != end; N1++) {
		//cout << "model.W "<j;
        ffm_int f1 = N1->f;
        ffm_float v1 = N1->v;
        if(j1 >= model.n || f1 >= model.m)
            continue;

        for(ffm_node *N2 = N1+1; N2 != end; N2++) {
            ffm_int j2 = N2->j;
            ffm_int f2 = N2->f;
            ffm_float v2 = N2->v;
            if(j2 >= model.n || f2 >= model.m)
                continue;

            ffm_float *w1 = model.W + (ffm_long)j1*align1 + f2*align0;
            ffm_float *w2 = model.W + (ffm_long)j2*align1 + f1*align0;

            ffm_float v = v1 * v2 * r;

            if(do_update) {
                ffm_float *wg1 = w1 + kALIGN;
                ffm_float *wg2 = w2 + kALIGN;
                for(ffm_int d = 0; d < align0; d += kALIGN * 2)
                {
                    ffm_float g1 = lambda * w1[d] + kappa * w2[d] * v;
                    ffm_float g2 = lambda * w2[d] + kappa * w1[d] * v;

                    wg1[d] += g1 * g1;
                    wg2[d] += g2 * g2;

                    w1[d] -= eta / sqrt(wg1[d]) * g1;
                    w2[d] -= eta / sqrt(wg2[d]) * g2;
                }
            } else {
                for(ffm_int d = 0; d < align0; d += kALIGN * 2)
                    t += w1[d] * w2[d] * v;
            }
        }
    }

    return t;
}

源码的一些问题：

问题1.ffm_node *end = &prob.X[prob.P[i+1]]下标越界问题

解决方法：

初始化时设置为(P[l]+1)

        P.resize(l+1);
        f.read(reinterpret_cast(P.data()), sizeof(ffm_long) * (l+1));

        X.resize(P[l]+1);
        f.read(reinterpret_cast(X.data()), sizeof(ffm_node) * (P[l]+1));

        ffm_long nnz = P[l];
        meta.l += l;

        f_bin.write(reinterpret_cast(&l), sizeof(ffm_int));
        f_bin.write(reinterpret_cast(Y.data()), sizeof(ffm_float) * l);
        f_bin.write(reinterpret_cast(R.data()), sizeof(ffm_float) * l);
        f_bin.write(reinterpret_cast(P.data()), sizeof(ffm_long) * (l+1));
        f_bin.write(reinterpret_cast(X.data()), sizeof(ffm_node) * (nnz+1));

问题2.ffm_model model = init_model(tr.meta.n, tr.meta.m, param);时model.K数据接不到

解决方法：

由于函数结束时析构函数会释放该内存数据，只能先停用析构函数

struct ffm_model {
    ffm_int n; // number of features
    ffm_int m; // number of fields
    ffm_int k; // number of latent factors
    ffm_float *W = nullptr;
    bool normalization;
    //~ffm_model();
};

/*
ffm_model::~ffm_model() {
    if(W != nullptr) {
#ifndef USESSE
        free(W);
#else
    #ifdef _WIN32
        _aligned_free(W);
    #else
        free(W);
    #endif
#endif
        W = nullptr;
    }
}
*/

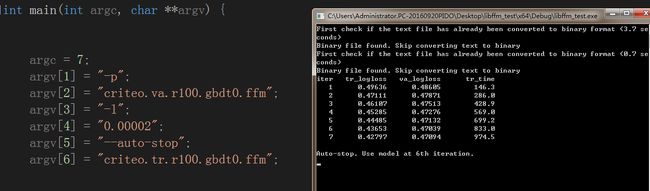
train测试截图

以及输出model（二进制文件）

不过你们不要轻易打开，看看大小就可以了。

四.总结

在DSP的场景中，FFM主要用来预估站内的CTR和CVR。在训练FFM的过程中，有许多小细节值得特别关注。
第一，样本归一化。FFM默认是进行样本数据的归一化，即 pa.normpa.norm 为真；若此参数设置为假，很容易造成数据inf溢出，进而引起梯度计算的nan错误。因此，样本层面的数据是推荐进行归一化的。
第二，特征归一化。CTR/CVR模型采用了多种类型的源特征，包括数值型和categorical类型等。但是，categorical类编码后的特征取值只有0或1，较大的数值型特征会造成样本归一化后categorical类生成特征的值非常小，没有区分性。例如，一条用户-商品记录，用户为“男”性，商品的销量是5000个（假设其它特征的值为零），那么归一化后特征“sex=male”（性别为男）的值略小于0.0002，而“volume”（销量）的值近似为1。特征“sex=male”在这个样本中的作用几乎可以忽略不计，这是相当不合理的。因此，将源数值型特征的值归一化到 [0,1][0,1] 是非常必要的。
第三，省略零值特征。从FFM模型的表达式(4)(4)可以看出，零值特征对模型完全没有贡献。包含零值特征的一次项和组合项均为零，对于训练模型参数或者目标值预估是没有作用的。因此，可以省去零值特征，提高FFM模型训练和预测的速度，这也是稀疏样本采用FFM的显著优势。

五.相关学习资源

https://tech.meituan.com/deep-understanding-of-ffm-principles-and-practices.html

http://blog.csdn.net/zc02051126/article/details/54614230

六.源码下载

官方源码：https://github.com/guestwalk/libffm  

VS2017工程（有些改动）：https://gitee.com/nine_sun/libffm_test

注：提供了FFM-predict.cpp预测和FFM-train.cpp训练两个接口