【目标跟踪】Long-term Correlation Tracking 阅读笔记

Long-term Correlation Tracking

论文地址：
https://www.cv-foundation.org/openaccess/content_cvpr_2015/papers/Ma_Long-Term_Correlation_Tracking_2015_CVPR_paper.pdf

long_term_tracking tracking 阅读笔记

---

简介

论文致力于解决在目标跟踪过程中，由于目标的外观变化，导致跟踪失败的问题。影响目标外观的因素包括目标本身形变、突然的快速移动、严重遮挡和出界等。解决的方法是把跟踪问题分解问平移估计和尺度变化估计。同时，时间上的上下文关系可以提高平移估计的精度，而训练判别相关滤波器（discriminative correlation filter）可以更有效地估计尺度变化。

本文提出的方法基于两个重要的前期工作：
首先，是对于视频而言，相邻的两帧变化很小。即便目标被遮挡了，其周围背景的变化也是很小的。所以，可以对跟踪目标本身和其周围背景同时进行建模，此模型提取的特征对严重遮挡、快速移动和严重形变都有很强的鲁棒性。
其次，是提高检测器的精度。这样可以更好地估计目标的尺度变化，以及当跟踪失败时重新检测。

另外，论文定义了 tracking-by-detection 的两个研究问题：
其一是稳定性-灵活性困境。也就是说，一个十分保守的模型，比如只对第一帧目标建模，这个模型一定十分鲁棒，不易引入背景噪声导致跟踪失败（drifting）。而一个积极更新的模型，就很容易跟丢，因为会引入背景噪声。文章提出的解决办法是对目标和背景分别建模，两个模型有不同的更新策略。
其二是负样本采集的问题。之前负样本采集十分模糊， 并且二分类的label对样本的空间关系的表达不够有效。本文采用Gaussian-weighted label来标注正负样本。

论文总的架构，是将长跟踪（long-term tracking）分解为对运动目标的尺度(scale) 和平移(translation) 的估计，并配合一个re-detection 策略。

相关工作和问题背景

相关滤波 Correlation tracking

相关滤波是一种应用非常广泛的方法，因为滤波操作可以通过频域上的乘法快速实现，所以它的优势在于极高的计算效率。例如 MOSSE(minimum output sum of squared error) 可以达到几百FPS。
但是这种方法的缺点在于，对在线的模型更新问题处理得不够好。很容易跟丢，以及难以应对遮挡和出界的问题。
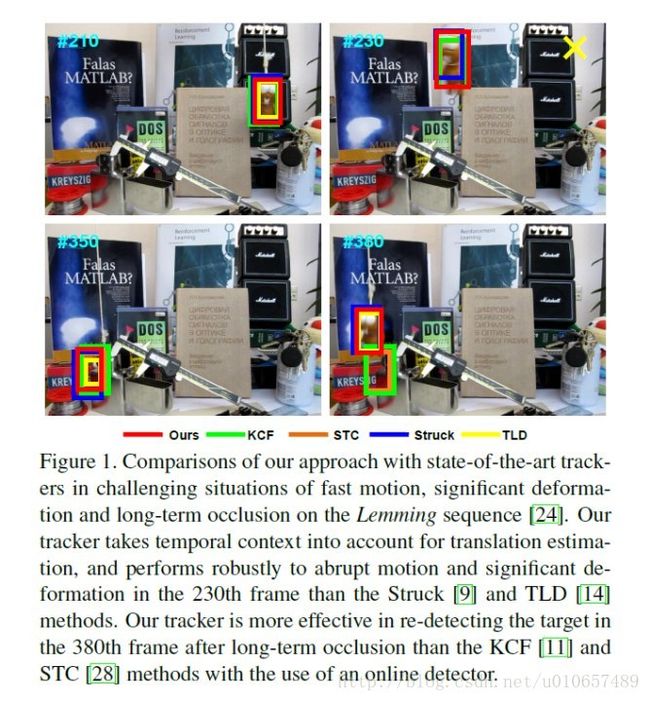
Figure1 展示了KCF算法的效果，可以看出来对于快速移动的物体，这种方法效果很好。但是当出现遮挡后，就跟丢了。(看绿框框，在230帧处出现了快速移动，跟踪效果很好。但是在350帧处出现了遮挡，到了380处目标再次出现，此时已经更新了模板，所以出现了drifting)

tracking-by-detection

为了解决稳定性-灵活性困境，Kalal 等人提出了 TLD(tracking, learning and detection)方法，提出跟踪和检测是可以互相促进的。跟踪为检测器提供正样本，检测器在跟踪失败时重新初始化跟踪器。
本文提出了一种方法，使用岭回归（ridge regression）模型来学习上下文的相关性，而不是简单地使用二分类模型。通过这种模型，可以有效减少二分类模型普遍出现的采样不明确的问题。

本文跟踪模块

本论文要解决的问题是，在跟踪过程中，跟踪目标出现较大的外观变化，可能导致跟踪失败。我们把跟踪问题分解为对目标的平移估计和尺度估计。其中，平移估计采用上下文相关性，尺度估计使用判别滤波器。此外，增加了一个检测器，用于在跟踪失败时的补充。

Correlation tracking

对于一个典型的相关滤波器而言，大体上流程是这样的：
对于一个 M×N M × N 大小的图像，其所有的循环矩阵 xm,n x m , n 作为训练样本。其label为 ym,n y m , n 。那么可以得到一个方程：

w=argminw∑m,n|ϕ(xm,n)⋅w−y(m,n)|2+λ|w|2 w = a r g m i n w ∑ m , n | ϕ ( x m , n ) ⋅ w − y ( m , n ) | 2 + λ | w | 2

其中 ϕ ϕ 表示到核空间的映射， λ λ 是正则化参数。（通过正则化项使矩阵满秩。）
使用快速傅里叶变换，把卷积操作变为elementwise的乘积操作。
求得使目标方程最小化的 w w 为：

w=∑m,na(m,n)ϕ(xm,n) w = ∑ m , n a ( m , n ) ϕ ( x m , n )

其中 a a 由下面公式得到：

A=F(a)=F(y)F(ϕ(x)⋅ϕ(x))+λ A = F ( a ) = F ( y ) F ( ϕ ( x ) ⋅ ϕ ( x ) ) + λ

F F 表示离散傅里叶变换。
接下来进行预测：
对于一张大小为 M×N M × N 新的图片 z z ， 计算响应图如下：

y^=F−1(A⊙F(ϕ(z)⋅ϕ(x^))) y ^ = F − 1 ( A ⊙ F ( ϕ ( z ) ⋅ ϕ ( x ^ ) ) )

其中， x^ x ^ 表示学习到的特征模型， ⊙ ⊙ 表示Hadamard product（其实就是element-wise product）。据此，预测这张图片上目标的位置，就通过找 y^ y ^ 上的最大值找到。

而本文使用的方法有一点点不同
首先，本文提出的方法是在同一张图像上学习两个filter。其中一个 Rc R c 同时考虑目标的特征和背景的特征，另一个 Rt R t 只考虑目标的特征。为了训练 Rc R c ，我们补充了一个空间权重。同时，为了减轻边界效应，对目标和上下文的响应加入余弦窗。
对于 Rc R c ，我们希望它能够及时更新，保证当目标遮挡、形变时能继续估算它的位移。所以，它需要一个较大的步长 α α 。亦即：

x^t=(1−α)x^t−1+αxtA^t=(1−α)A^t−1+αAt x ^ t = ( 1 − α ) x ^ t − 1 + α x t A ^ t = ( 1 − α ) A ^ t − 1 + α A t

其中t 为当前帧的index。
判别模型 Rt R t 在比较可靠的帧上习得。所谓比较可靠的帧，就是 y^ y ^ 最大值比较高的帧。（也就是说，和之前的模板匹配程度更高的帧）我们定义一个阈值 Ta T a , 只有当 y^ y ^ 的最大值大于 Ta T a 时才更新模板。（当目标发生遮挡时，不会更改filter）
在预测位置附近构造一个金字塔。令目标的大小为 P×Q P × Q ，金字塔层数为 N N ，则 S={an|n=⌊−N−12⌋,⌊−N−32⌋,...,⌊N+12⌋} S = { a n | n = ⌊ − N − 1 2 ⌋ , ⌊ − N − 3 2 ⌋ , . . . , ⌊ N + 1 2 ⌋ }
对于 s∈S s ∈ S ， 选取预测位置中心的 sP×sQ s P × s Q 区域， resize到 P×Q P × Q 大小。然后提取HOG特征。
然后取响应最大值：

s^=argmaxs{max(y^1),max(y^2),...,max(y^s)} s ^ = a r g m a x s { m a x ( y ^ 1 ) , m a x ( y ^ 2 ) , . . . , m a x ( y ^ s ) }

则当 max(y^s^)>Ta m a x ( y ^ s ^ ) > T a 时更新 Rt R t

Online Detector

当跟踪失败，我们需要使用一个检测器重新初始化跟踪器。那么，就需要知道什么时候跟踪就失败了。我们这里设置了第二个阈值 Tb T b ，如果 max(y^s^)<Tb m a x ( y ^ s ^ ) < T b 时重新检测。

算法流程

• 输入：
  初始化目标检测框
• 输出：
  预测的目标状态（state）： Xt=(x^t,y^t,s^t) X t = ( x ^ t , y ^ t , s ^ t )
  两个回归模型 Rc,Rt R c , R t ， 一个检测器 Drf D r f

• repeat:
  根据 (xt−1,yt−1) ( x t − 1 , y t − 1 ) 在第t帧上选取检索范围（seraching window） 并提取特征
  //平移估计
  使用 RC R C 计算响应 Yt Y t ，并估计当前帧位置 (xt,yt) ( x t , y t )
  //尺度估计
  在 (xt,yt) ( x t , y t ) 附近构造图像金字塔，计算相关响应 ys y s .
  使用 Rt R t 估计最佳尺度 s^ s ^
  //此时，得到了第t帧的状态 (xt,yt,st) ( x t , y t , s t )
  //重新检测
  如果 max(y^s^)<Tb m a x ( y ^ s ^ ) < T b ：
  {
  调用检测器重新检测
  如果检测得分大于阈值，则更新轨迹
  }

  //更新模型
  更新 Rc R c
  如果 max(y^s^)>Ta m a x ( y ^ s ^ ) > T a ：
  {
  更新 Rt R t
  }
  更新检测器

• 如果视频序列结束，停止循环