二叉查找树（BST）：概念、基本操作和性能分析

二叉查找树 (Binary Search Tree, BST) 是二叉树在查找中的一种重要应用形式。

在这篇文章接下来的叙述中，做出以下假设：

• 尽管二叉树节点中存储的数据类型是任意的，但为了大小比较和理解的方便，本文中将数据类型指定为整数。
• 各个节点中的存储的数据是没有重复的。

定义

若一棵二叉树为二叉查找树，那么它必须满足：

• 对于树中的任意节点 $X$，若其左子树不为空，则左子树中每一个节点的值都小于其根节点的值
• 对于树中的任意节点 $X$，若其右子树不为空，则右子树中每一个节点的值都大于或等于其根节点的值
• 对于树中的任意节点 $X$，其左子树、右子树也为二叉查找树

这是一个明显带有递归特征的定义。根据这个定义，下面给出一个正确的 BST 示例和两个错误的 BST 实例。

声明

我们给出 BST 的类型定义并列出 BST 的一系列基本操作，如下即为 BST 的声明程序。

typedef int ElementType;

struct TreeNode;
typedef struct TreeNode *Position;
typedef struct TreeNode *SearchTree;

/*BST 的基本操作定义 */
SearchTree MakeEmpty(SearchTree T);
Position Find(ElementType X, SearchTree T);
Position FindMin(SearchTree T);
Position FindMax(SearchTree T);
SearchTree Insert(ElementType X, SearchTree T);
SearchTree Delete(ElementType X, SearchTree T);
ElementType Retrieve(Position P);

/* 单个树节点的结构体定义 */
struct TreeNode
{
     
    ElementType Element;
    SearchTree Left;
    SearchTree Right;
};

接下来我们将对 BST 的基本操作进行逐一实现。

基本操作

初始化 MakeEmpty

该操作用于初始化树 $T$。

事实上，我们可以把 BST 的第一个元素初始化为一个单节点树，但是下面给出的初始化代码是一种更加遵循递归原则的形式（如 BST 的定义一样）。

/* 初始化一棵树 T*/
SearchTree MakeEmpty(SearchTree T)
{
     
    if (T != NULL)
    {
     
        MakeEmpty(T->Left);
        MakeEmpty(T->Right);
        free(T);
    }
    return NULL;
}

查找任意值 Find

该操作用于返回给定的树 $T$ 中值为 $X$ 的节点的指针。若不存在则返回 NULL。

/* 对树 T 查找值 X 的位置 */
Position Find(ElementType X, SearchTree T)
{
     
    if (T == NULL)
        return NULL;
    if (X < T->Element)
        return Find(X, T->Left);
    else if (X> T->Element)
        return Find(X, T->Right);
    else
        return T;
}

如果树 $T$ 本身为 NULL，则直接返回 NULL。否则根据所寻值 X 与当前节点值的大小关系对左子树或右子树进行递归调用，若找到相等值即返回。

查找最小/最大值 FindMin/FindMax

与查找任意值 $X$ 的 Find 操作类似，查找最小/最大值的程序可以很容易地利用递归的思想写出来。

下面的例程中阐释了 FindMin 操作的递归实现：从根节点出发，不断地向左寻找左子树（这是由于 BST 的性质），最终找到的就是最小的元素。FindMax 操作仅在寻找的方向上有所不同。

/*FindMin 操作的递归实现 */
Position FindMin(SearchTree T)
{
     
    if(T == NULL)
        return NULL;
    else
    if(T->Left == NULL)
        return T;
    else
        return FindMin(T->Left);
}

事实上，查找最小 / 最大值的操作使用非递归的思想实现也是非常简单的，下面是 FindMin 操作的非递归实现。

/*FindMin 操作的非递归实现 */
Position FindMin(SearchTree T)
{
     
    if(T != NULL)
        while(T->Left != NULL)
            T = T->Left;

    return T;
}

插入 Insert

在查找操作的基础上，我们很容易实现 BST 的插入操作，其本质上就是在树 $T$ 中寻找适合待插值 $X$ 的位置：如果在树 $T$ 中找到了 $X$，那么不执行操作（或者执行特定的更新操作）；如果树 $T$ 中不存在 $X$，那么，Find 操作最终找到的位置就是适合 $X$ 的位置。

/* 将值 X 插入到二叉查找树 T 中 */
SearchTree Insert(ElementType X, SearchTree T)
{
     
    if (T == NULL)
    {
     
        T = malloc(sizeof(struct TreeNode));
        if (T == NULL)
            return NULL; /*Out of space*/
        else
        {
     
            T->Element = X;
            T->Left = T->Right = NULL;
        }
    }
    else if (X < T->Element)
        T->Left = Insert(X, T->Left);
    else if (X> T->Element)
        T->Right = Insert(X, T->Right);

    return T;
}

有了上面的 Insert 操作，我们就可以用一段简单的程序来构造一棵 BST 了，像下面这样：

int i;
int a[7] = {
     67, 73, 129, 25, 101, 310, 123};
SearchTree *T = NULL;
for (i = 0; i < 7; i++)
{
     
    Insert(a[i], T);
}

删除 Delete

与前面的操作相比，从一棵 BST 中删除一个节点是最困难的，因为我们需要保证删除节点后的新树依然满足 BST 的性质。因此我们需要将可能存在的情况进行分类考虑。

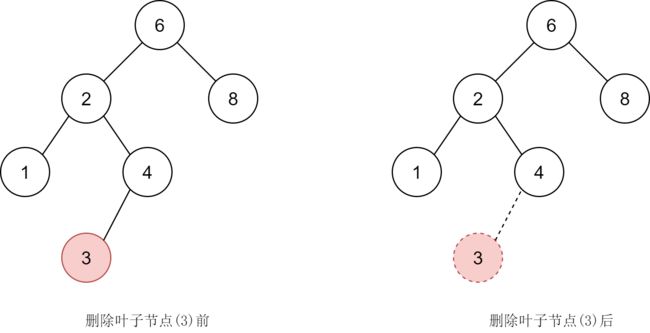
首先是最简单的情况：要删除的节点是一个叶子节点，这时可以直接删除该节点，下面是这种情况的示意图。

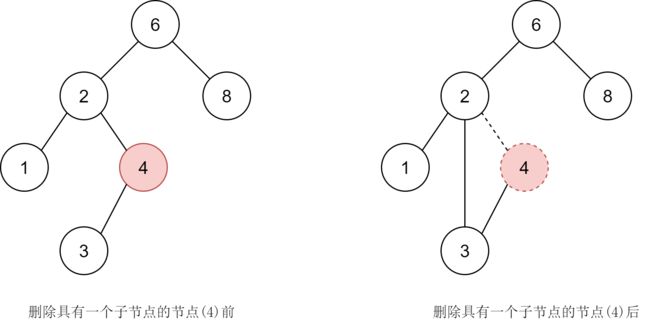
其次是待删除节点 $N$ 有一个子节点的情况，这时需要将其父节点 $N_{parent}$ 连接至待删除节点 $N$ 的子节点 $N_{child}$ 后，再对待删除节点执行删除，下面是这种情况的示意图。

最复杂的情况是待删除的节点 $N$ 有两个子节点 $N_{lchild}$ 和 $N_{rchild}$，这时，通常采用的删除方法是，找到以 $N_{rchild}$ 为根节点的右子树中数据最小的节点 $N_{rmin}$ 来替代 $N$，然后递归地删除 $N_{rmin}$。
举个例子，在下左的 BST 中删除具有两个子节点的节点 (2)，根据上述的删除方法，删除的结果就是，(2) 的右子树中的最小节点 (3) 替代了 (2)，并且原 (3) 节点被删除。

根据上面的思路，可以得到如下的删除操作代码：

/* 从树 T 中删除值为 X 的节点 */
SearchTree Delete(ElementType X, SearchTree T)
{
     
    Position TmpCell;

    if (T == NULL)
        Error("Element not found");
    else if (X < T->Element)
        T->Left = Delete(X, T->Left);
    else if (X> T->Element)
        T->Right = Delete(X, T->Right);
    else
        if (T->Left && T->Right)
        {
     
            TmpCell = FindMin(T->Right);
            T->Element = TmpCell->Element;
            T->Right = Delete(T->Element, T->Right);
        }
    else
    {
     
        TmpCell = T;
        if (T->Left == NULL)
            T = T->Right;
        else if (T->Right == NULL)
            T = T->Left;
        free(TmpCell);
    }
    return T;
}

性能分析

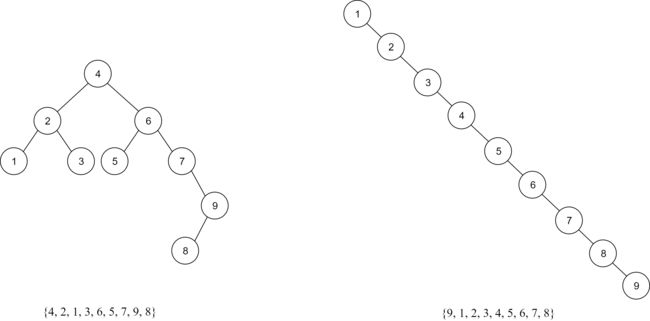
考虑两个元素内容相同但顺序不同的序列：{4, 2, 1, 3, 6, 5, 7, 9, 8} 和 {1, 2, 3, 4, 5, 6, 7, 8, 9}，下图展示了两种序列得到的 BST，前一种得到的是一个相对「平衡」的 BST，而后一种，其构造序列是严格从小到大排列的，于是得到的 BST 是一种极端的右斜树。

在这两个不同的树上考虑 BST 的查找、插入和删除操作，很容易得出结论：BST 各项操作的复杂度和树的拓扑结构有着密切的联系。以查找操作为例，在左树中查找节点 (7) 仅需两次查找，而右树中则需要 7 次。

因此在树的结构上，我们希望 BST 是比较「平衡」的，其中最优的情况是，由 $n$ 个元素构成的 BST 的高度 $h$ 与其构成的完全二叉树高度相等，即满足 $h=\lfloor \log n\rfloor +1$，最差的情况类似上图右树所示，其高度满足 $h=n$。

与之对应，查找、删除、插入算法的复杂度最优情况下为 $O(\log n)$，最坏情况下为 $O(n)$。

这里也引出了一个问题，即如何使二叉树更加平衡，这涉及到一种古老的平衡查找树：AVL 树，将在下一篇做介绍。

参考资料

[1] (美)Mark Allen Weiss. 数据结构与算法分析: C 语言描述 [M]. 机械工业出版社: 北京, 2017:73-80.
[2] 程杰. 大话数据结构 [M]. 清华大学出版社: 北京, 2011:313-328.
[3] 维基百科：二叉搜索树 [EB/OL].https://zh.wikipedia.org/wiki/二叉搜索树,2020-2-14.