游戏中掉落效果的实现

1. 计算运动参数

 运动特征： 竖直方向受到重力作用，水平方向有空气阻力作用

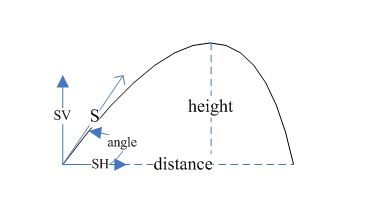
 第一种情况： 起抛点位置和掉落点位置处于同一水平面中。已知开始抛起的点位置和掉落目标位置，由此可以求出两点之间的距离 distance；

 运动轨迹如下所示：

                             

 ①根据rand 函数产生出[0,1]之间的数值，作为运动总的时间。并且heigt 也可以根据则会个随机值扩大些，作为运动的高度

      t = seed()

      height = 16 * seed() * seed();

 ②根据 sV/2 * t/2 = heght, 可以求出 sV

       sV = 4*height / 4

 ③ 根据 sV = g * (t/2)  . 求出

      g= 2*sV /t;

  ④ 假设，水平方向，受到空气阻力的作用，速度会减少，减少到 0.75 sH， 则根据水平方向速度距离关系，可以推导

     (sH + 0.75 sH)/2 * t = distance       =>     sH = (8/7) * distance /  t 

      进一步，可以知道水平方向的减速度

      hg = 0.25* sH / t

  这样，就可以实时计算出运动的位置了

  Vector3 tDist = dirDistance * (initSpeedH * t - 0.5f * hVelocity * t * t);
tDist.y += initSpeedV * t- gVelocity * t * t * 0.5f;

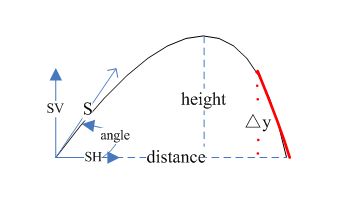
第二种情况：起跑点和掉落点不是处于同一水平面中

                                  

这个时候，需要把红色部分给加上来，才是完整的运动轨迹。即确定红色那部分运动时间，以及水平方向运动距离

① 第一种情况中的①②③ ，因为计算都是用的运动的前半部分，都是一样的。根据y 的差值结合计算出来变量，可以知道花费的时间

   tAdd= Math::pow(2 * △y / g,  0.5f);

② 整个运动时间，也要加上刚才计算出来的时间

     t = t + tAdd;

 ③ 同样假设，水平方向，受到空气阻力的作用，速度会减少，减少到 0.75 sH， 则根据水平方向速度距离关系，可以推导

     (sH + 0.75 sH)/2 * (t+tAdd) = distance       =>     sH = (8/7) * distance /  (t+tAdd) 

      进一步，可以知道水平方向的减速度

      hg = 0.25* sH /(t+tAdd) 

  这样，就可以实时计算出运动的位置了

  Vector3 tDist = dirDistance * (initSpeedH * t - 0.5f * hVelocity * t * t);
tDist.y += initSpeedV * t- gVelocity * t * t * 0.5f;

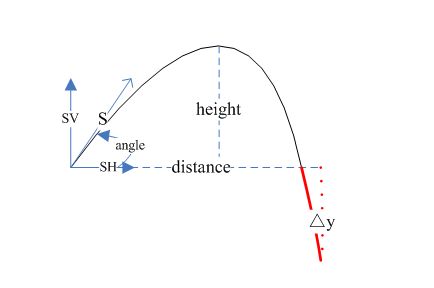
第三种情况 如下所示，掉落到坑里去了；此时，同样需要计算出那部分运动的时间，tMus, 并减去这部分时间，来计算水平方向的减速度

                        

源码如下：

bool GoodsFallEffect::calcData(Vector3 & startPos,Vector3 & endPos)
{
	if (!mRecord)
	{
	    return false;
	}

	mContext.dirDistance = endPos - startPos;
	float length = mContext.dirDistance.length();
	mContext.dirDistance.normalize();

	float cx = length;
	float cy = 0;
	float seed = rnd();
	float height =10*seed *seed;//*Math::Pow(seed,0.5f);;

        float t= seed;    // second units
	
	float n = 2 * height;   //得到解

	
	if (cx > 0)
	{

	   if(endPos.y - startPos.y <3.0f)
	    {
		mContext.initSpeedH = 1.3f * length / t;
		mContext.initSpeedV = 4*height /t;
		mContext.gVelocity = 2* mContext.initSpeedV / t;
		mContext.angle = atanf(mContext.initSpeedV / mContext.initSpeedH);
		mContext.initSpeed = Math::Pow(mContext.initSpeedH * mContext.initSpeedH + mContext.initSpeedV * mContext.initSpeedV, 0.5f);
		mContext.hVelocity = 0.5f *mContext.initSpeedH / t;
		mContext.maxHightTime = t*500.0f;
		mContext.sumTime = t*1000.0f;
	    }
	   else
	   {
		mContext.initSpeedV = 4*height /t;
		mContext.gVelocity = 2*mContext.initSpeedV / t;
          
		float devia = Math::Abs(endPos.y - startPos.y);
		float tAdd = Math::Pow(2*devia / mContext.gVelocity, 0.5f);
		// 此处有个近视，length
		if(endPos.y > startPos.y)
		{
                    mContext.initSpeedH = 1.3f * length / (t+tAdd);
		    mContext.maxHightTime = (t+tAdd)*500.0f;
	            mContext.sumTime = (t+tAdd)*1000.0f;
		}
		else
		{
                    mContext.initSpeedH = 1.3f * length / (t-tAdd);
	            mContext.maxHightTime = (t-tAdd)*500.0f;
		    mContext.sumTime = (t-tAdd)*1000.0f;
		}
	  }
	}
	else
	{
	   mContext.initSpeedH = 0;
	   mContext.angle = PI/2.0f;
	   mContext.initSpeed = 20/seed;
	}
	Vector3 tDist = mContext.dirDistance *(mContext.initSpeedH * t *0.5f - 0.5f * mContext.hVelocity * 0.5f * t * 0.5f * t);
        mContext.rotateAxis= Vector3(height * mContext.dirDistance.z - tDist.z * mContext.dirDistance.y, tDist.z * mContext.dirDistance.x - tDist.x * mContext.dirDistance. z, tDist.x * mContext.dirDistance.y - height *mContext.dirDistance. x);

	return true;
}

2. 旋转

   运动参数计算好了，需要控制物品的的旋转，模拟自然物品抛起来的自转。此时采用四元数的旋转，关键在于旋转轴的选择。

   这里我们选择抛物线所在平面的法向量作为旋转轴。 取抛物线上两个点向量做叉乘,此处选择最高点和水平点；

    Vector3 tDist = dirDistance *(initSpeedH * t *0.5f - 0.5f * hVelocity * 0.5f * t * 0.5f * t);
    rotateAxis= Vector3(height * dirDistance.z - tDist.z * dirDistance.y, tDist.z * dirDistance.x - tDist.x * dirDistance. z, tDist.x * dirDistance.y - height *dirDistance. x);
           ...
    node->rotate(mContext.rotateAxis,mAngle);

3. 大小变化

   控制抛起过程中物品的逐渐变大，下降过程中的逐渐减小

     配置文件中配置物品抛起来刚开始的minSize，最高点的maxSize， 如果上升中，即运动时间runTime < t/2   ; 既可以

    if(mRunTime < maxHightTime){
           f = (float)mRunTime/(float)mContext.maxHightTime;
           scale = mContext.startScale + f*(mContext.maxHightScale - mContext.startScale);
           scale = Clamp(scale,0.0f,mContext.maxHightScale);
       }

      同样的下降过程中也是可以类似的处理。

最后贴几张图。。