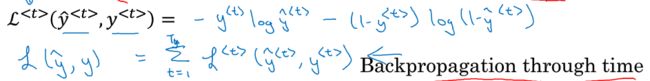Andrew Ng Deep Learning 第五课 第一周
Andrew Ng Deep Learning 第五课 第一周
- 前言
- 循环序列模型
- 为什么选择循环序列模型
- 循环神经网络(RNN)
- 数字符号
- 网络模型
- 通过时间的反向传播
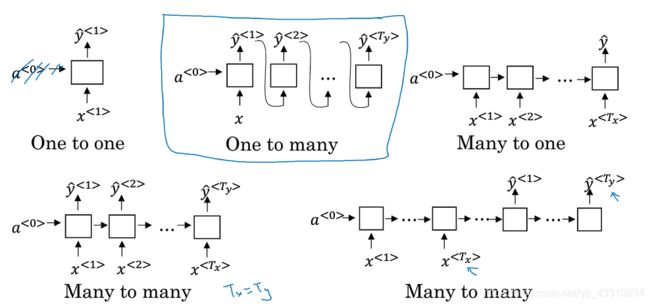
- 不同类型的RNN
- 编程作业
- 语言模型与序列生成
- 编程作业
- 梯度消失
- GRU单元
- LSTM
- 编程作业
- 双向神经网络
- 深层RNN
- 课后选择题
前言
网易云课堂(双语字幕,不卡):https://mooc.study.163.com/smartSpec/detail/1001319001.htmcourseId=1004570029、
Coursera(贵):https://www.coursera.org/specializations/deep-learning
本人初学者,先在网易云课堂上看网课,再去Coursera上做作业,开博客以记录,文章中引用图片皆为课程中所截。
题目转载至:http://www.cnblogs.com/hezhiyao/p/7810725.html
编程作业所需库:链接:https://pan.baidu.com/s/1aS1Oia2fskemBHHEMnSepw 密码:66gd
循环序列模型
为什么选择循环序列模型

Tips:适用于x与y有一个是序列模型或者都是序列模型的情况(x与y长度不同并且不同样本x长度方式也不同)
循环神经网络(RNN)
数字符号

Tips:序列模型(识别单词)第一件事是制作一张单词表,对于每个x


Tips:单词表也有单词和字符两种选择方式
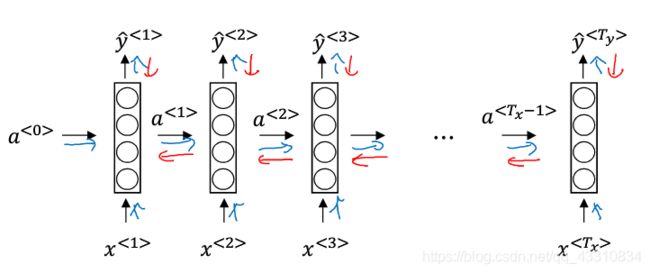
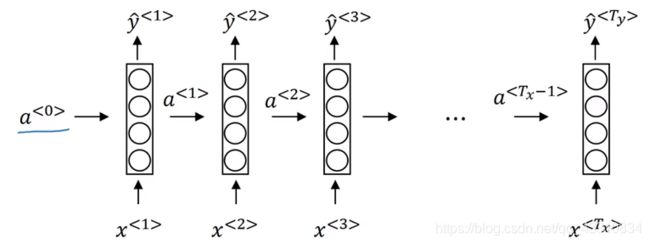
网络模型
Tips:a
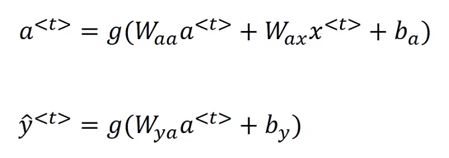

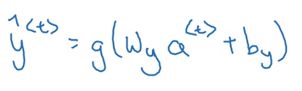
Tips:此处Waa和Wax和ba都是参数矩阵,将前两者横向堆叠成Wa矩阵,将a和x纵向堆叠成[a,x]矩阵,这此处的g为激活函数。这就构成了RNN的正向传播
通过时间的反向传播
不同类型的RNN
编程作业
import numpy as np
import rnn_utils
def rnn_cell_forward(xt, a_prev, parameters):
"""
根据图2实现RNN单元的单步前向传播
参数:
xt -- 时间步“t”输入的数据,维度为(n_x, m)
a_prev -- 时间步“t - 1”的隐藏隐藏状态,维度为(n_a, m)
parameters -- 字典,包含了以下内容:
Wax -- 矩阵,输入乘以权重,维度为(n_a, n_x)
Waa -- 矩阵,隐藏状态乘以权重,维度为(n_a, n_a)
Wya -- 矩阵,隐藏状态与输出相关的权重矩阵,维度为(n_y, n_a)
ba -- 偏置,维度为(n_a, 1)
by -- 偏置,隐藏状态与输出相关的偏置,维度为(n_y, 1)
返回:
a_next -- 下一个隐藏状态,维度为(n_a, m)
yt_pred -- 在时间步“t”的预测,维度为(n_y, m)
cache -- 反向传播需要的元组,包含了(a_next, a_prev, xt, parameters)
"""
# Retrieve parameters from "parameters"
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
### START CODE HERE ### (≈2 lines)
# compute next activation state using the formula given above
a_next=np.tanh(np.dot(Wax,xt)+np.dot(Waa,a_prev)+ba)
yt_pred=rnn_utils.softmax(np.dot(Wya,a_next)+by)
# compute output of the current cell using the formula given above
### END CODE HERE ###
# store values you need for backward propagation in cache
cache = (a_next, a_prev, xt, parameters)
return a_next, yt_pred, cache
def rnn_forward(x, a0, parameters):
"""
根据图3来实现循环神经网络的前向传播
参数:
x -- 输入的全部数据,维度为(n_x, m, T_x)
a0 -- 初始化隐藏状态,维度为 (n_a, m)
parameters -- 字典,包含了以下内容:
Wax -- 矩阵,输入乘以权重,维度为(n_a, n_x)
Waa -- 矩阵,隐藏状态乘以权重,维度为(n_a, n_a)
Wya -- 矩阵,隐藏状态与输出相关的权重矩阵,维度为(n_y, n_a)
ba -- 偏置,维度为(n_a, 1)
by -- 偏置,隐藏状态与输出相关的偏置,维度为(n_y, 1)
返回:
a -- 所有时间步的隐藏状态,维度为(n_a, m, T_x)
y_pred -- 所有时间步的预测,维度为(n_y, m, T_x)
caches -- 为反向传播的保存的元组,维度为(【列表类型】cache, x))
"""
# Initialize "caches" which will contain the list of all caches
caches = []
# Retrieve dimensions from shapes of x and parameters["Wya"]
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
### START CODE HERE ###
# initialize "a" and "y" with zeros (≈2 lines)
a=np.zeros([n_a,m,T_x])
y=np.zeros([n_y,m,T_x])
# Initialize a_next (≈1 line)
a_next=a0
# loop over all time-steps
for t in range(T_x):
# Update next hidden state, compute the prediction, get the cache (≈1 line)
a_next, yt_pred, cache=rnn_cell_forward(x[:,:,t], a_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t]=a_next
# Save the value of the prediction in y (≈1 line)
y[:,:,t]=yt_pred
# Append "cache" to "caches" (≈1 line)
caches.append(cache)
### END CODE HERE ###
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y, caches
语言模型与序列生成
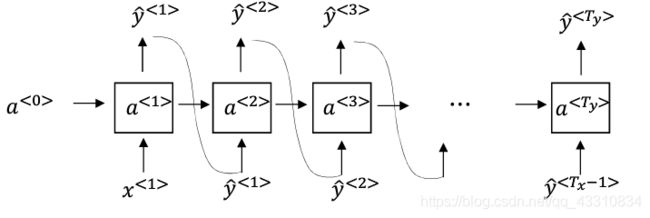
Tips:在RNN的基础上,使得每个输入x都与上个输出y相等,这样假设输入一句话时,每个单词都与前面的单词相关联
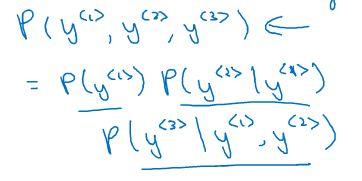
Tips:即每一步P(Yi)=P(Yi,Yi-1…)的前提下,在案例中即为知道前面的词为xxx和yyy的前提下计算下一个词是什么的概率
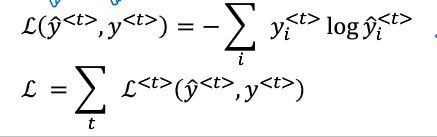
用这个技术就可以打造新序列

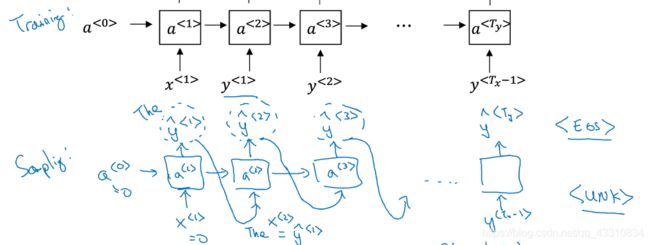
Tips:用语言模型的方法,先对一个完整的样本进行训练,然后用训练完的模型由0开始自我生成(输入零向量,由模型得到y<1>的概率,对softmax结果采用随机采样,得到输出结果y<1>,然后将y<1>作为输入进行下一个时间步的训练得到y<2>)
编程作业
import numpy as np
import random
import time
import cllm_utils
# 获取名称
data = open("dinos.txt", "r").read()
# 转化为小写字符
data = data.lower()
# 转化为无序且不重复的元素列表
chars = list(set(data))
# 获取大小信息
data_size, vocab_size = len(data), len(chars)
print(chars)
print("共计有%d个字符,唯一字符有%d个"%(data_size,vocab_size))
char_to_ix = {ch:i for i, ch in enumerate(sorted(chars))}
ix_to_char = {i:ch for i, ch in enumerate(sorted(chars))}
print(char_to_ix)
print(ix_to_char)
def sample(parameters, char_to_is, seed):
"""
根据RNN输出的概率分布序列对字符序列进行采样
参数:
parameters -- 包含了Waa, Wax, Wya, by, b的字典
char_to_ix -- 字符映射到索引的字典
seed -- 随机种子
返回:
indices -- 包含采样字符索引的长度为n的列表。
"""
# Retrieve parameters and relevant shapes from "parameters" dictionary
Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
vocab_size = by.shape[0] # vocab_size 指字典的大小
n_a = Waa.shape[1]
### START CODE HERE ###
# Step 1: Create the one-hot vector x for the first character (initializing the sequence generation). (≈1 line)
x=np.zeros([vocab_size,1]) # x 是 one hot 向量
# Step 1': Initialize a_prev as zeros (≈1 line)
a_prev=np.zeros([n_a,1]) # a_prev 是 (n_a,1) 维向量
# Create an empty list of indices, this is the list which will contain the list of indices of the characters to generate (≈1 line)
indices=[]
# Idx is a flag to detect a newline character, we initialize it to -1
idx=-1
# Loop over time-steps t. At each time-step, sample a character from a probability distribution and append
# its index to "indices". We'll stop if we reach 50 characters (which should be very unlikely with a well
# trained model), which helps debugging and prevents entering an infinite loop.
counter = 0
newline_character = char_to_ix["\n"]
while (idx != newline_character and counter < 50):
# Step 2: Forward propagate x using the equations (1), (2) and (3)
a=np.tanh(np.dot(Wax,x)+np.dot(Waa,a_prev)+b)
z=np.dot(Wya,a)+by
y=cllm_utils.softmax(z)
# for grading purposes
np.random.seed(counter+seed)
# Step 3: Sample the index of a character within the vocabulary from the probability distribution y
# np.arange(vocab_size) 返回一个一维数组,即[0,1,...,vocab_size]
# np.random.choice(vocab_size,p=y.ravel()) 等价于 np.random.choice([0,1,...,vocab_size],p=y.ravel())
idx = np.random.choice(vocab_size, p=y.ravel())
# Append the index to "indices"
indices.append(idx)
# Step 4: Overwrite the input character as the one corresponding to the sampled index.
# 根据取样索引值修改x,即将索引对应的one hot向量的位置值改为1
x=np.zeros(([vocab_size,1]))
x[idx]=1
# Update "a_prev" to be "a"
a_prev=a
# for grading purposes
seed+=1
counter+=1
### END CODE HERE ###
if (counter == 50):
indices.append(char_to_ix['\n'])
return indices
def optimize(X, Y, a_prev, parameters, learning_rate = 0.01):
"""
执行训练模型的单步优化。
参数:
X -- 整数列表,其中每个整数映射到词汇表中的字符。
Y -- 整数列表,与X完全相同,但向左移动了一个索引。
a_prev -- 上一个隐藏状态
parameters -- 字典,包含了以下参数:
Wax -- 权重矩阵乘以输入,维度为(n_a, n_x)
Waa -- 权重矩阵乘以隐藏状态,维度为(n_a, n_a)
Wya -- 隐藏状态与输出相关的权重矩阵,维度为(n_y, n_a)
b -- 偏置,维度为(n_a, 1)
by -- 隐藏状态与输出相关的权重偏置,维度为(n_y, 1)
learning_rate -- 模型学习的速率
返回:
loss -- 损失函数的值(交叉熵损失)
gradients -- 字典,包含了以下参数:
dWax -- 输入到隐藏的权值的梯度,维度为(n_a, n_x)
dWaa -- 隐藏到隐藏的权值的梯度,维度为(n_a, n_a)
dWya -- 隐藏到输出的权值的梯度,维度为(n_y, n_a)
db -- 偏置的梯度,维度为(n_a, 1)
dby -- 输出偏置向量的梯度,维度为(n_y, 1)
a[len(X)-1] -- 最后的隐藏状态,维度为(n_a, 1)
"""
### START CODE HERE ###
# Forward propagate through time (≈1 line)
loss, cache =cllm_utils.rnn_forward(X, Y, a_prev, parameters)
# Backpropagate through time (≈1 line)
gradients, a = cllm_utils.rnn_backward(X, Y, parameters, cache)
# Clip your gradients between -5 (min) and 5 (max) (≈1 line)
gradients = clip(gradients,5)
# Update parameters (≈1 line)
parameters = cllm_utils.update_parameters(parameters, gradients, learning_rate)
### END CODE HERE ###
return loss, gradients, a[len(X)-1]
def model(data, ix_to_char, char_to_ix, num_iterations=3500,
n_a=50, dino_names=7,vocab_size=27):
"""
训练模型并生成恐龙名字
参数:
data -- 语料库
ix_to_char -- 索引映射字符字典
char_to_ix -- 字符映射索引字典
num_iterations -- 迭代次数
n_a -- RNN单元数量
dino_names -- 每次迭代中采样的数量
vocab_size -- 在文本中的唯一字符的数量
返回:
parameters -- 学习后了的参数
"""
# 从vocab_size中获取n_x、n_y
n_x, n_y = vocab_size, vocab_size
# 初始化参数
parameters = cllm_utils.initialize_parameters(n_a, n_x, n_y)
# 初始化损失
loss = cllm_utils.get_initial_loss(vocab_size, dino_names)
# 构建恐龙名称列表
with open("dinos.txt") as f:
examples = f.readlines()
examples = [x.lower().strip() for x in examples]
# 打乱全部的恐龙名称
np.random.seed(0)
np.random.shuffle(examples)
# 初始化LSTM隐藏状态
a_prev = np.zeros((n_a,1))
# 循环
for j in range(num_iterations):
# 定义一个训练样本
index = j % len(examples)
X = [None] + [char_to_ix[ch] for ch in examples[index]]
Y = X[1:] + [char_to_ix["\n"]]
# 执行单步优化:前向传播 -> 反向传播 -> 梯度修剪 -> 更新参数
# 选择学习率为0.01
curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters)
# 使用延迟来保持损失平滑,这是为了加速训练。
loss = cllm_utils.smooth(loss, curr_loss)
# 每2000次迭代,通过sample()生成“\n”字符,检查模型是否学习正确
if j % 2000 == 0:
print("第" + str(j+1) + "次迭代,损失值为:" + str(loss))
seed = 0
for name in range(dino_names):
# 采样
sampled_indices = sample(parameters, char_to_ix, seed)
cllm_utils.print_sample(sampled_indices, ix_to_char)
# 为了得到相同的效果,随机种子+1
seed += 1
print("\n")
return parameters
#开始时间
start_time = time.clock()
#开始训练
parameters = model(data, ix_to_char, char_to_ix, num_iterations=3500)
#结束时间
end_time = time.clock()
#计算时差
minium = end_time - start_time
print("执行了:" + str(int(minium / 60)) + "分" + str(int(minium%60)) + "秒")
#开始时间
start_time = time.clock()
from keras.callbacks import LambdaCallback
from keras.models import Model, load_model, Sequential
from keras.layers import Dense, Activation, Dropout, Input, Masking
from keras.layers import LSTM
from keras.utils.data_utils import get_file
from keras.preprocessing.sequence import pad_sequences
from shakespeare_utils import *
import sys
import io
#结束时间
end_time = time.clock()
#计算时差
minium = end_time - start_time
print("执行了:" + str(int(minium / 60)) + "分" + str(int(minium%60)) + "秒")
print_callback = LambdaCallback(on_epoch_end=on_epoch_end)
model.fit(x, y, batch_size=128, epochs=1, callbacks=[print_callback])
# 运行此代码尝试不同的输入,而不必重新训练模型。
generate_output()
梯度消失
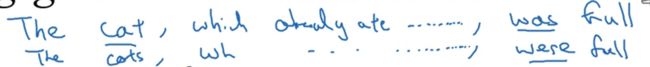
Tips:出现这种序列模型的时候,需要模型具有长时间记忆能力。
GRU单元

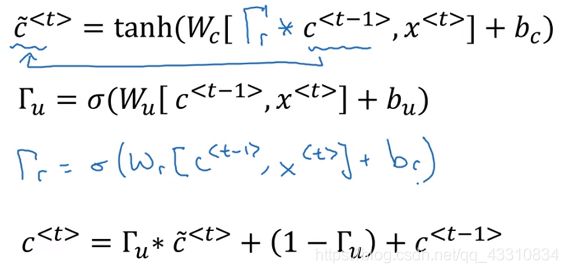
Tips:定义一个新的传递参数c(记忆细胞),定义一个更新参数Γu和相关参数 Γr,将c一步步传递,传递需要输入上一个c即上一个神经元输出的a和当前模型输入x,激活函数为sigmoid(因为Γ保持在0-1之间)。该模型能使RNN具有长期记忆能力,参数c为一个向量,向量中不同的位置的参数定义了不同的记忆点,比如第一个位置记忆句子中主语的单复数形式,第二个位置定义了句子中提到的动词等等。

Tips:比如说在这句话中,假设模型训练到cat时,c
LSTM
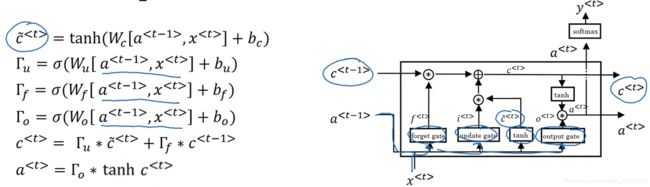
Tips:相比GRU,LSTM多了一个Γo(输出门),使得输出a有了变化,计算下一层的c的时候使用的是上一层的输出a(此时不等于上一层的输出c)
编程作业
import numpy as np
import rnn_utils
def lstm_cell_forward(xt, a_prev, c_prev, parameters):
"""
根据图4实现一个LSTM单元的前向传播。
参数:
xt -- 在时间步“t”输入的数据,维度为(n_x, m)
a_prev -- 上一个时间步“t-1”的隐藏状态,维度为(n_a, m)
c_prev -- 上一个时间步“t-1”的记忆状态,维度为(n_a, m)
parameters -- 字典类型的变量,包含了:
Wf -- 遗忘门的权值,维度为(n_a, n_a + n_x)
bf -- 遗忘门的偏置,维度为(n_a, 1)
Wi -- 更新门的权值,维度为(n_a, n_a + n_x)
bi -- 更新门的偏置,维度为(n_a, 1)
Wc -- 第一个“tanh”的权值,维度为(n_a, n_a + n_x)
bc -- 第一个“tanh”的偏置,维度为(n_a, n_a + n_x)
Wo -- 输出门的权值,维度为(n_a, n_a + n_x)
bo -- 输出门的偏置,维度为(n_a, 1)
Wy -- 隐藏状态与输出相关的权值,维度为(n_y, n_a)
by -- 隐藏状态与输出相关的偏置,维度为(n_y, 1)
返回:
a_next -- 下一个隐藏状态,维度为(n_a, m)
c_next -- 下一个记忆状态,维度为(n_a, m)
yt_pred -- 在时间步“t”的预测,维度为(n_y, m)
cache -- 包含了反向传播所需要的参数,包含了(a_next, c_next, a_prev, c_prev, xt, parameters)
注意:
ft/it/ot表示遗忘/更新/输出门,cct表示候选值(c tilda),c表示记忆值。
"""
# Retrieve parameters from "parameters"
Wf = parameters["Wf"]
bf = parameters["bf"]
Wi = parameters["Wi"]
bi = parameters["bi"]
Wc = parameters["Wc"]
bc = parameters["bc"]
Wo = parameters["Wo"]
bo = parameters["bo"]
Wy = parameters["Wy"]
by = parameters["by"]
# Retrieve dimensions from shapes of xt and Wy
n_x, m = xt.shape
n_y, n_a = Wy.shape
### START CODE HERE ###
# Concatenate a_prev and xt (≈3 lines)
contact=np.zeros(([n_x+n_a,m]))
contact[:n_a,:]=a_prev
contact[n_a:,:]=xt
# xt -- your input data at timestep "t", numpy array of shape (n_x, m).
# a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
# Compute values for ft, it, cct, c_next, ot, a_next using the formulas given figure (4) (≈6 lines)
ft=rnn_utils.sigmoid(np.dot(Wf,contact)+bf)
it=rnn_utils.sigmoid(np.dot(Wi,contact)+bi)
cct=np.tanh(np.dot(Wc,contact)+bc)
c_next=ft*c_prev+it*cct
ot=rnn_utils.sigmoid(np.dot(Wo,contact)+bo)
a_next=ot*np.tanh(c_next)
# Compute prediction of the LSTM cell (≈1 line)
yt_prev=rnn_utils.softmax(np.dot(Wy,a_next)+by)
### END CODE HERE ###
# store values needed for backward propagation in cache
cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
return a_next, c_next, yt_prev, cache
def lstm_forward(x, a0, parameters):
"""
根据图5来实现LSTM单元组成的的循环神经网络
参数:
x -- 所有时间步的输入数据,维度为(n_x, m, T_x)
a0 -- 初始化隐藏状态,维度为(n_a, m)
parameters -- python字典,包含了以下参数:
Wf -- 遗忘门的权值,维度为(n_a, n_a + n_x)
bf -- 遗忘门的偏置,维度为(n_a, 1)
Wi -- 更新门的权值,维度为(n_a, n_a + n_x)
bi -- 更新门的偏置,维度为(n_a, 1)
Wc -- 第一个“tanh”的权值,维度为(n_a, n_a + n_x)
bc -- 第一个“tanh”的偏置,维度为(n_a, n_a + n_x)
Wo -- 输出门的权值,维度为(n_a, n_a + n_x)
bo -- 输出门的偏置,维度为(n_a, 1)
Wy -- 隐藏状态与输出相关的权值,维度为(n_y, n_a)
by -- 隐藏状态与输出相关的偏置,维度为(n_y, 1)
返回:
a -- 所有时间步的隐藏状态,维度为(n_a, m, T_x)
y -- 所有时间步的预测值,维度为(n_y, m, T_x)
caches -- 为反向传播的保存的元组,维度为(【列表类型】cache, x))
"""
# Initialize "caches", which will track the list of all the caches
caches = []
### START CODE HERE ###
# Retrieve dimensions from shapes of x and parameters['Wy'] (≈2 lines)
n_x,m,T_x=x.shape
n_y,n_a=parameters['Wy'].shape
# initialize "a", "c" and "y" with zeros (≈3 lines)
a=np.zeros([n_a,m,T_x])
c=np.zeros([n_a,m,T_x])
y=np.zeros([n_y,m,T_x])
# Initialize a_next and c_next (≈2 lines)
a_next=a0
c_next=np.zeros([n_a,m])
# loop over all time-steps
for t in range(T_x):
# Update next hidden state, next memory state, compute the prediction, get the cache (≈1 line)
a_next, c_next, yt_prev, cache=lstm_cell_forward(x[:,:,t], a_next, c_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t]=a_next
# Save the value of the prediction in y (≈1 line)
y[:,:,t]=yt_prev
# Save the value of the next cell state (≈1 line)
c[:,:,t]=c_next
# Append the cache into caches (≈1 line)
caches.append(cache)
### END CODE HERE ###
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y, c, caches
from keras.models import load_model, Model
from keras.layers import Dense, Activation, Dropout, Input, LSTM, Reshape, Lambda, RepeatVector
from keras.initializers import glorot_uniform
from keras.utils import to_categorical
from keras.optimizers import Adam
from keras import backend as K
import numpy as np
import IPython
import sys
IPython.display.Audio('./data/30s_seq.mp3')
from music21 import *
from grammar import *
from qa import *
from preprocess import *
from music_utils import *
from data_utils import *
reshapor = Reshape((1, 78)) #2.B
LSTM_cell = LSTM(n_a, return_state = True) #2.C
densor = Dense(n_values, activation='softmax') #2.D
X, Y, n_values, indices_values = load_music_utils()
def djmodel(Tx, n_a, n_values):
"""
实现这个模型
参数:
Tx -- 语料库的长度
n_a -- 激活值的数量
n_values -- 音乐数据中唯一数据的数量
返回:
model -- Keras模型实体
"""
# Define the input of your model with a shape
X = Input(shape=(Tx, n_values))
# Define s0, initial hidden state for the decoder LSTM
a0 = Input(shape=(n_a,), name='a0')
c0 = Input(shape=(n_a,), name='c0')
a = a0
c = c0
### START CODE HERE ###
# Step 1: Create empty list to append the outputs while you iterate (≈1 line)
outputs=[]
# Step 2: Loop
for t in range(Tx):
# Step 2.A: select the "t"th time step vector from X.
x = Lambda(lambda x: X[:,t,:])(X)
# Step 2.B: Use reshapor to reshape x to be (1, n_values) (≈1 line)
x = reshapor(x)
# Step 2.C: Perform one step of the LSTM_cell
a, _, c = LSTM_cell(x, initial_state=[a, c])
# Step 2.D: Apply densor to the hidden state output of LSTM_Cell
out = densor(a)
# Step 2.E: add the output to "outputs"
outputs.append(out)
# Step 3: Create model instance
model = Model(inputs=[X, a0, c0], outputs=outputs)
### END CODE HERE ###
return model
# 获取模型,这里Tx=30, n_a=64,n_values=78
model = djmodel(Tx = 30 , n_a = 64, n_values = 78)
# 编译模型,我们使用Adam优化器与分类熵损失。
opt = Adam(lr=0.01, beta_1=0.9, beta_2=0.999, decay=0.01)
model.compile(optimizer=opt, loss='categorical_crossentropy', metrics=['accuracy'])
# 初始化a0和c0,使LSTM的初始状态为零。
m = 60
n_a = 64
a0 = np.zeros((m, n_a))
c0 = np.zeros((m, n_a))
import time
#开始时间
start_time = time.clock()
#开始拟合
model.fit([X, a0, c0], list(Y), epochs=100)
#结束时间
end_time = time.clock()
#计算时差
minium = end_time - start_time
print("执行了:" + str(int(minium / 60)) + "分" + str(int(minium%60)) + "秒")
def music_inference_model(LSTM_cell, densor, n_values = 78, n_a = 64, Ty = 100):
"""
参数:
LSTM_cell -- 来自model()的训练过后的LSTM单元,是keras层对象。
densor -- 来自model()的训练过后的"densor",是keras层对象
n_values -- 整数,唯一值的数量
n_a -- LSTM单元的数量
Ty -- 整数,生成的是时间步的数量
返回:
inference_model -- Kears模型实体
"""
# Define the input of your model with a shape
x0 = Input(shape=(1, n_values))
# Define s0, initial hidden state for the decoder LSTM
a0 = Input(shape=(n_a,), name='a0')
c0 = Input(shape=(n_a,), name='c0')
a = a0
c = c0
x = x0
### START CODE HERE ###
# Step 1: Create an empty list of "outputs" to later store your predicted values (≈1 line)
outputs = []
# Step 2: Loop over Ty and generate a value at every time step
for t in range(Ty):
# Step 2.A: Perform one step of LSTM_cell (≈1 line)
a, _, c = LSTM_cell(x, initial_state=[a, c])
# Step 2.B: Apply Dense layer to the hidden state output of the LSTM_cell (≈1 line)
out = densor(a)
# Step 2.C: Append the prediction "out" to "outputs". out.shape = (None, 78) (≈1 line)
outputs.append(out)
# Step 2.D: Select the next value according to "out", and set "x" to be the one-hot representation of the
# selected value, which will be passed as the input to LSTM_cell on the next step. We have provided
# the line of code you need to do this.
x = Lambda(one_hot)(out)
# Step 3: Create model instance with the correct "inputs" and "outputs" (≈1 line)
inference_model = Model([x0, a0, c0], outputs)
### END CODE HERE ###
return inference_model
# 获取模型实体,模型被硬编码以产生50个值
inference_model = music_inference_model(LSTM_cell, densor, n_values = 78, n_a = 64, Ty = 50)
#创建用于初始化x和LSTM状态变量a和c的零向量。
x_initializer = np.zeros((1, 1, 78))
a_initializer = np.zeros((1, n_a))
c_initializer = np.zeros((1, n_a))
def predict_and_sample(inference_model, x_initializer = x_initializer, a_initializer = a_initializer,
c_initializer = c_initializer):
"""
使用模型预测当前值的下一个值。
参数:
inference_model -- keras的实体模型
x_initializer -- 初始化的独热编码,维度为(1, 1, 78)
a_initializer -- LSTM单元的隐藏状态初始化,维度为(1, n_a)
c_initializer -- LSTM单元的状态初始化,维度为(1, n_a)
返回:
results -- 生成值的独热编码向量,维度为(Ty, 78)
indices -- 所生成值的索引矩阵,维度为(Ty, 1)
"""
### START CODE HERE ###
# Step 1: Use your inference model to predict an output sequence given x_initializer, a_initializer and c_initializer.
pred = inference_model.predict([x_initializer, a_initializer, c_initializer])
# Step 2: Convert "pred" into an np.array() of indices with the maximum probabilities
indices = np.argmax(pred,axis=2)
# Step 3: Convert indices to one-hot vectors, the shape of the results should be (1, )
results = to_categorical(indices)
### END CODE HERE ###
return results, indices
results, indices = predict_and_sample(inference_model, x_initializer, a_initializer, c_initializer)
print("np.argmax(results[12]) =", np.argmax(results[12]))
print("np.argmax(results[17]) =", np.argmax(results[17]))
print("list(indices[12:18]) =", list(indices[12:18]))
out_stream = generate_music(inference_model)
双向神经网络

Tips:有些情况下,要判断某单词是否是主语的时候需要借助的不仅是前面单词,而且需要后面所有单词
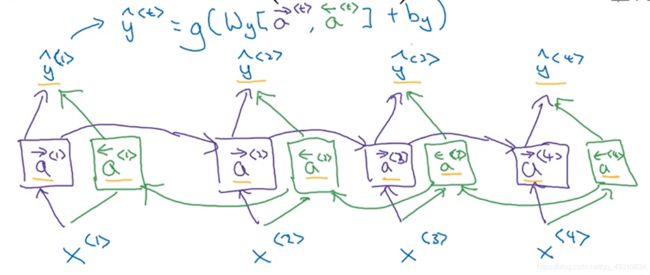
Tips:构建双向函数a,使得每一个输出y都经过了双向传播得到的结果a,即对某单词的预测经过了前后单词的共同作用
深层RNN
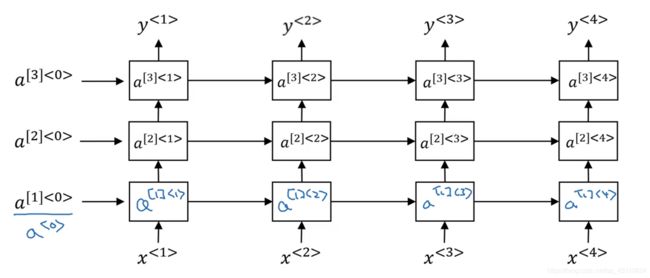
Tips:相比单层网络,计算每一层y的时候增加了两层a,使得每层有三个参数a需要传递给下一层
课后选择题


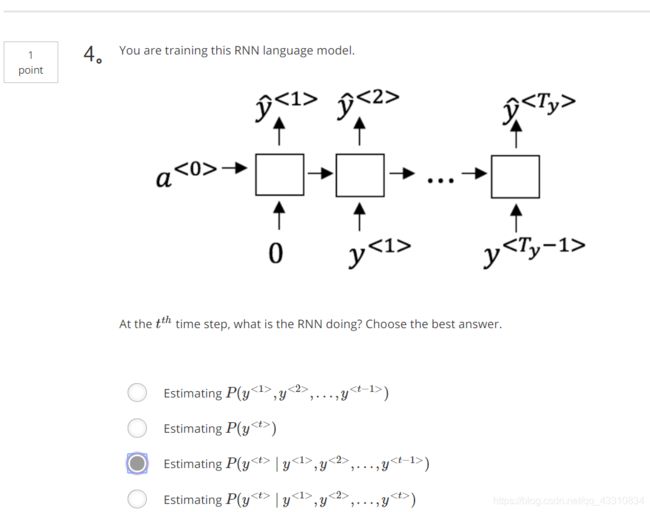

Tips:对每个位置的y的softmax预测中,不是采用最大值的确认方式,而是随机采样(np.random.choice)
Tips:Γu的向量维度等于LSTM中隐藏单元的数量,因为要标定每一个单元需不需要更新c