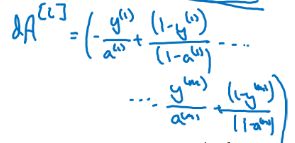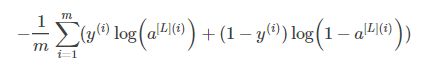Andrew Ng Deep Learning 第一课
Andrew Ng Deep Learning 第一课
- 前言
- 神经网络基础与浅层神经网络(该基础部分与Machine Learning内容基本重复)
- 1.二元分类
- 2.向量化logistic回归
- 编程作业
- 3.向量化单隐藏层神经网络
- 编程作业
- 4.激活函数
- 5.向量化深层神经网络
- 编程作业
- 6.步骤总结
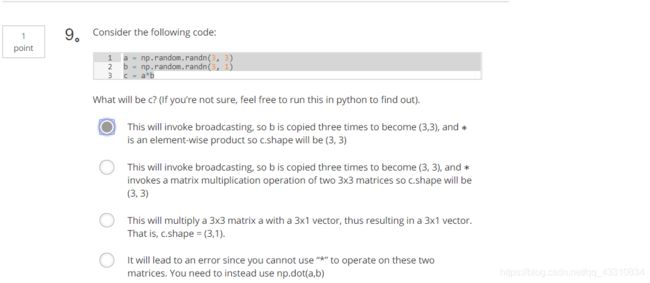
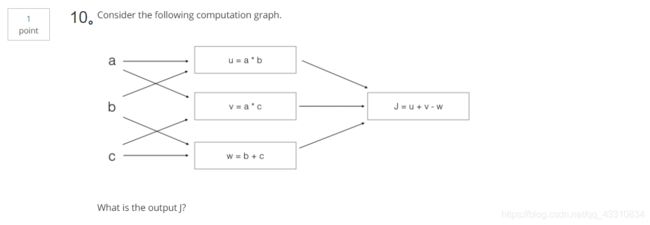
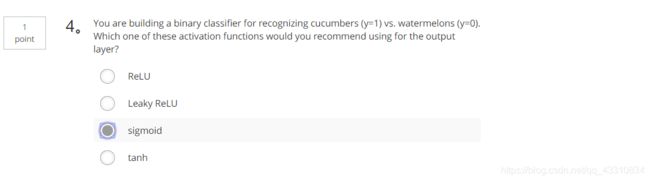
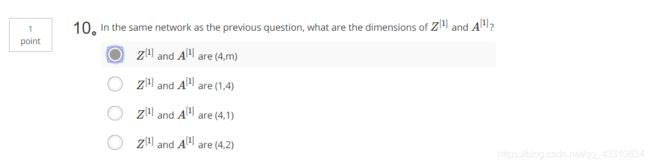
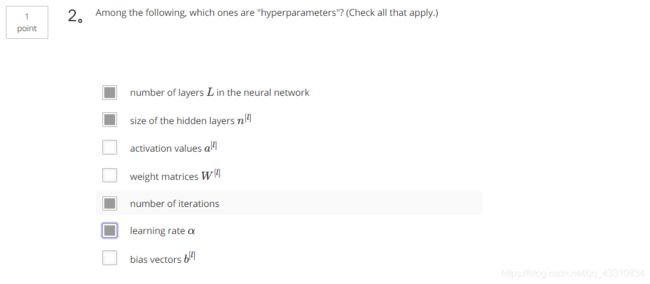
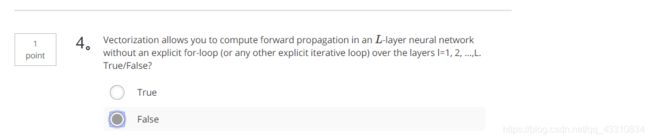
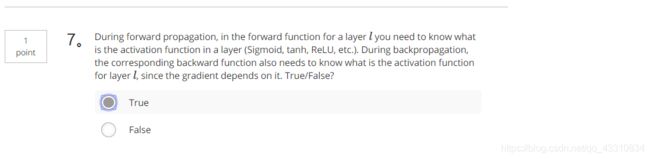
- 题目
- 1.Question 1
- 2.Question 2
- 3.Question 3
前言
网易云课堂(双语字幕,不卡):https://mooc.study.163.com/smartSpec/detail/1001319001.htmcourseId=1004570029、
Coursera(贵):https://www.coursera.org/specializations/deep-learning
本人初学者,先在网易云课堂上看网课,再去Coursera上做作业,开博客以记录,文章中引用图片皆为课程中所截。
题目转载至:http://www.cnblogs.com/hezhiyao/p/7810725.html
编程作业所需库:链接:https://pan.baidu.com/s/1aS1Oia2fskemBHHEMnSepw 密码:66gd
神经网络基础与浅层神经网络(该基础部分与Machine Learning内容基本重复)
1.二元分类
2.向量化logistic回归



Tips:初始化w为均为0的nx维列向量,b为0,X是nx × m矩阵,w是nx × 1系数矩阵,b是实数,Y是1 × m结果矩阵,dZ是当前计算的h(x)与结果值的差值矩阵,dw是系数变换矩阵,α是学习率,最后进行sigmoid(np.dot(w.T,X)+b)预判最终结果即y=P(y=1|x)
编程作业
def sigmoid(z):
"""
参数:
z - 任何大小的标量或numpy数组。
返回:
s - sigmoid(z)
"""
s = 1 / (1 + np.exp(-z))
return s
def initialize_with_zeros(dim):
"""
此函数为w创建一个维度为(dim,1)的0向量,并将b初始化为0。
参数:
dim - 我们想要的w矢量的大小(或者这种情况下的参数数量)
返回:
w - 维度为(dim,1)的初始化向量。
b - 初始化的标量(对应于偏差)
"""
w = np.zeros(shape = (dim,1))
b = 0
return (w , b)
def propagate(w, b, X, Y):
"""
实现前向和后向传播的成本函数及其梯度。
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 矩阵类型为(num_px * num_px * 3,训练数量)
Y - 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据数量)
返回:
cost- 逻辑回归的负对数似然成本
dw - 相对于w的损失梯度,因此与w相同的形状
db - 相对于b的损失梯度,因此与b的形状相同
"""
m=X.shape[1]
z=np.dot(w.T,X)+b
a=sigmoid(z)
cost=np.sum(Y*np.log(a)+(1-Y)*np.log(1-a))
cost/=(-m)
dz=a-Y
dw=np.dot(X,dz.T)
dw/=m
db=np.sum(dz)
db/=m
return (cost , dw ,db)
def optimize(w , b , X , Y , num_iterations , learning_rate , print_cost = False):
"""
此函数通过运行梯度下降算法来优化w和b
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 维度为(num_px * num_px * 3,训练数据的数量)的数组。
Y - 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据的数量)
num_iterations - 优化循环的迭代次数
learning_rate - 梯度下降更新规则的学习率
print_cost - 每100步打印一次损失值
返回:
params - 包含权重w和偏差b的字典
grads - 包含权重和偏差相对于成本函数的梯度的字典
成本 - 优化期间计算的所有成本列表,将用于绘制学习曲线。
提示:
我们需要写下两个步骤并遍历它们:
1)计算当前参数的成本和梯度,使用propagate()。
2)使用w和b的梯度下降法则更新参数。
"""
costs=[]
for i in range(num_iterations):
cost,dw,db=propagate(w, b, X, Y)
w=w-learning_rate*dw
b=b-learning_rate*db
if i % 100 == 0:
costs.append(cost)
if (print_cost) and (i % 100 == 0):
print("迭代的次数: %i , 误差值: %f" % (i,cost))
params = {
"w" : w,
"b" : b }
grads = {
"dw": dw,
"db": db }
return params,grads,costs
def predict(w , b , X ):
"""
使用学习逻辑回归参数logistic (w,b)预测标签是0还是1,
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 维度为(num_px * num_px * 3,训练数据的数量)的数据
返回:
Y_prediction - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组(向量)
"""
Y_prediction=sigmoid(np.dot(w.T,X)+b)
return np.round(Y_prediction)
def model(X_train , Y_train , X_test , Y_test , num_iterations = 2000 , learning_rate = 0.5 , print_cost = False):
"""
通过调用之前实现的函数来构建逻辑回归模型
参数:
X_train - numpy的数组,维度为(num_px * num_px * 3,m_train)的训练集
Y_train - numpy的数组,维度为(1,m_train)(矢量)的训练标签集
X_test - numpy的数组,维度为(num_px * num_px * 3,m_test)的测试集
Y_test - numpy的数组,维度为(1,m_test)的(向量)的测试标签集
num_iterations - 表示用于优化参数的迭代次数的超参数
learning_rate - 表示optimize()更新规则中使用的学习速率的超参数
print_cost - 设置为true以每100次迭代打印成本
返回:
d - 包含有关模型信息的字典。
"""
w , b = initialize_with_zeros(X_train.shape[0])
parameters , grads , costs = optimize(w , b , X_train , Y_train,num_iterations , learning_rate , print_cost)
#从字典“参数”中检索参数w和b
w , b = parameters["w"] , parameters["b"]
#预测测试/训练集的例子
Y_prediction_test = predict(w , b, X_test)
Y_prediction_train = predict(w , b, X_train)
#打印训练后的准确性
print("训练集准确性:" , format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100) ,"%")
print("测试集准确性:" , format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100) ,"%")
d = {
"costs" : costs,
"Y_prediction_test" : Y_prediction_test,
"Y_prediciton_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations" : num_iterations }
return d
3.向量化单隐藏层神经网络



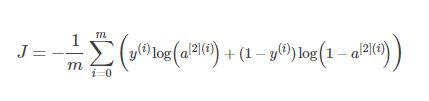
Tips:第一步随机初始化W和b,w[i]为(n[i],n[i-1])矩阵,b[i]为(n[i],1)矩阵,z[i]为(n[i],1)矩阵,之后对于m个样本,将每个W,b,z都以列向量形式堆叠成(x,m)矩阵(此处x为单个样本的矩阵大小),首先进行正向传播计算,然后进行反向传播计算导数后进行梯度下降
编程作业
import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
#%matplotlib inline #如果你使用用的是Jupyter Notebook的话请取消注释。
np.random.seed(1) #设置一个固定的随机种子,以保证接下来的步骤中我们的结果是一致的。
X, Y = load_planar_dataset()
shape_X = X.shape
shape_Y = Y.shape
m = Y.shape[1] # 训练集里面的数量
def layer_sizes(X , Y):
"""
参数:
X - 输入数据集,维度为(输入的数量,训练/测试的数量)
Y - 标签,维度为(输出的数量,训练/测试数量)
返回:
n_x - 输入层的数量
n_h - 隐藏层的数量
n_y - 输出层的数量
"""
n_x = X.shape[0]
n_h = 4
n_y = Y.shape[0]
return (n_x,n_h,n_y)
def initialize_parameters( n_x , n_h ,n_y):
"""
参数:
n_x - 输入层节点的数量
n_h - 隐藏层节点的数量
n_y - 输出层节点的数量
返回:
parameters - 包含参数的字典:
W1 - 权重矩阵,维度为(n_h,n_x)
b1 - 偏向量,维度为(n_h,1)
W2 - 权重矩阵,维度为(n_y,n_h)
b2 - 偏向量,维度为(n_y,1)
"""
W1 = np.random.randn(n_h,n_x) * 0.01
b1 = np.zeros(shape=(n_h, 1))
W2 = np.random.randn(n_y,n_h) * 0.01
b2 = np.zeros(shape=(n_y, 1))
parameters = {"W1" : W1,
"b1" : b1,
"W2" : W2,
"b2" : b2 }
return parameters
def forward_propagation( X , parameters ):
"""
参数:
X - 维度为(n_x,m)的输入数据。
parameters - 初始化函数(initialize_parameters)的输出
返回:
A2 - 使用sigmoid()函数计算的第二次激活后的数值
cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典类型变量
"""
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
Z1 = np.dot(W1,X)+b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2,A1)+b2
A2 = sigmoid(Z2)
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return (A2, cache)
def compute_cost(A2,Y,parameters):
"""
计算方程(6)中给出的交叉熵成本,
参数:
A2 - 使用sigmoid()函数计算的第二次激活后的数值
Y - "True"标签向量,维度为(1,数量)
parameters - 一个包含W1,B1,W2和B2的字典类型的变量
返回:
成本 - 交叉熵成本给出方程(13)
"""
pass
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
logprobs=np.dot(np.log(A2),Y.T)+np.dot(np.log((1-A2)),(1-Y).T)
cost = - np.sum(logprobs) / m
cost = float(np.squeeze(cost))
return cost
def backward_propagation(parameters,cache,X,Y):
"""
使用上述说明搭建反向传播函数。
参数:
parameters - 包含我们的参数的一个字典类型的变量。
cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典类型的变量。
X - 输入数据,维度为(2,数量)
Y - “True”标签,维度为(1,数量)
返回:
grads - 包含W和b的导数一个字典类型的变量。
"""
m = X.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
A1 = cache["A1"]
A2 = cache["A2"]
'''
w2=n2,n1 z2=n2,1
n1,1
'''
dZ2=A2-Y
dW2=np.dot(dZ2,A1.T)/m
db2=np.sum(dZ2,axis=1,keepdims=True)/m
dZ1=np.dot(W2.T,dZ2)* (1 - np.power (A1, 2) )
dW1=np.dot(dZ1,X.T)/m
db1=np.sum(dZ1,axis=1,keepdims=True)/m
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2 }
return grads
def update_parameters(parameters,grads,learning_rate=1.2):
"""
使用上面给出的梯度下降更新规则更新参数
参数:
parameters - 包含参数的字典类型的变量。
grads - 包含导数值的字典类型的变量。
learning_rate - 学习速率
返回:
parameters - 包含更新参数的字典类型的变量。
"""
W1,W2 = parameters["W1"],parameters["W2"]
b1,b2 = parameters["b1"],parameters["b2"]
dW1,dW2 = grads["dW1"],grads["dW2"]
db1,db2 = grads["db1"],grads["db2"]
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
def nn_model(X,Y,n_h,num_iterations,print_cost=False):
"""
参数:
X - 数据集,维度为(2,示例数)
Y - 标签,维度为(1,示例数)
n_h - 隐藏层的数量
num_iterations - 梯度下降循环中的迭代次数
print_cost - 如果为True,则每1000次迭代打印一次成本数值
返回:
parameters - 模型学习的参数,它们可以用来进行预测。
"""
np.random.seed(3) #指定随机种子
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
parameters = initialize_parameters(n_x,n_h,n_y)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
for i in range(num_iterations):
A2 , cache = forward_propagation(X,parameters)
cost = compute_cost(A2,Y,parameters)
grads = backward_propagation(parameters,cache,X,Y)
parameters = update_parameters(parameters,grads,learning_rate = 0.5)
if print_cost:
if i%1000 == 0:
print("第 ",i," 次循环,成本为:"+str(cost))
return parameters
def predict(parameters,X):
"""
使用学习的参数,为X中的每个示例预测一个类
参数:
parameters - 包含参数的字典类型的变量。
X - 输入数据(n_x,m)
返回
predictions - 我们模型预测的向量(红色:0 /蓝色:1)
"""
A2 , cache = forward_propagation(X,parameters)
predictions = np.round(A2)
return predictions
parameters = nn_model(X, Y, n_h = 4, num_iterations=10000, print_cost=True)
#绘制边界
#plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
#plt.title("Decision Boundary for hidden layer size " + str(4))
predictions = predict(parameters, X)
print ('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
4.激活函数

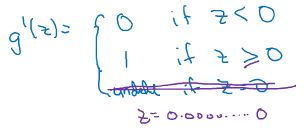

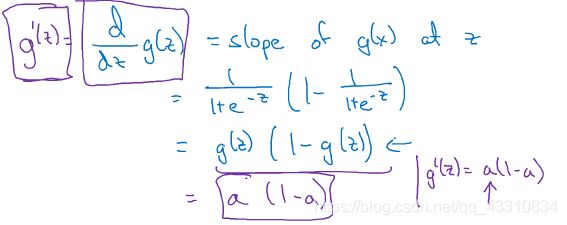
Tips:非二元分类的隐藏层单元使用RELU,二元分类的输出单元使用sigmoid
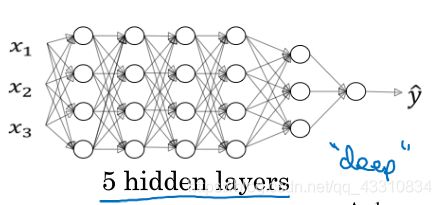
5.向量化深层神经网络
Tips:dA[l-1]为l-1层的成本梯度,dA[L]为向后传播的初始化dA,整体步骤与浅层神经网络相似,多了一步对每层使用for循环进行向前传播和向后传播
编程作业
import numpy as np
import h5py
from skimage.transform import resize
from scipy import ndimage
import matplotlib.pyplot as plt
import testCases #参见资料包,或者在文章底部copy
from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward #参见资料包
import lr_utils #参见资料包,或者在文章底部copy
def initialize_parameters(n_x,n_h,n_y):
"""
此函数是为了初始化两层网络参数而使用的函数。
参数:
n_x - 输入层节点数量
n_h - 隐藏层节点数量
n_y - 输出层节点数量
返回:
parameters - 包含你的参数的python字典:
W1 - 权重矩阵,维度为(n_h,n_x)
b1 - 偏向量,维度为(n_h,1)
W2 - 权重矩阵,维度为(n_y,n_h)
b2 - 偏向量,维度为(n_y,1)
"""
### START CODE HERE ### (≈ 4 lines of code)
W1=np.random.randn(n_h,n_x)*0.01
b1=np.zeros((n_h,1))
W2=np.random.rand(n_y,n_h)*0.01
b2=np.zeros((n_y,1))
### END CODE HERE ###
assert(W1.shape == (n_h, n_x))
assert(b1.shape == (n_h, 1))
assert(W2.shape == (n_y, n_h))
assert(b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
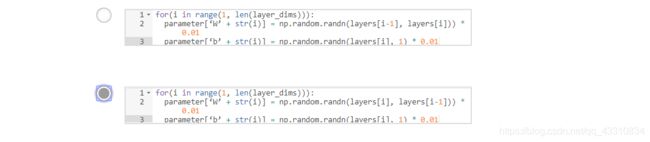
def initialize_parameters_deep(layer_dims):
"""
此函数是为了初始化多层网络参数而使用的函数。
参数:
layers_dims - 包含我们网络中每个图层的节点数量的列表
返回:
parameters - 包含参数“W1”,“b1”,...,“WL”,“bL”的字典:
W1 - 权重矩阵,维度为(layers_dims [1],layers_dims [1-1])
bl - 偏向量,维度为(layers_dims [1],1)
"""
parameters={}
L = len(layer_dims) # number of layers in the network
for l in range(1, L):
### START CODE HERE ### (≈ 2 lines of code)
parameters['W'+str(l)]=np.random.randn(layers_dims[l], layers_dims[l - 1]) / np.sqrt(layers_dims[l - 1])
parameters['b'+str(l)]=np.zeros((layer_dims[l],1))
### END CODE HERE ###
assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1]))
assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))
return parameters
def linear_forward(A,W,b):
"""
实现前向传播的线性部分。
参数:
A - 来自上一层(或输入数据)的激活,维度为(上一层的节点数量,示例的数量)
W - 权重矩阵,numpy数组,维度为(当前图层的节点数量,前一图层的节点数量)
b - 偏向量,numpy向量,维度为(当前图层节点数量,1)
返回:
Z - 激活功能的输入,也称为预激活参数
cache - 一个包含“A”,“W”和“b”的字典,存储这些变量以有效地计算后向传递
"""
### START CODE HERE ### (≈ 1 line of code)
Z=np.dot(W,A)+b
### END CODE HERE ###
assert(Z.shape == (W.shape[0], A.shape[1])) # W的行数,Z的列数
cache = (A, W, b)
return Z, cache
def linear_activation_forward(A_prev,W,b,activation):
"""
实现LINEAR-> ACTIVATION 这一层的前向传播
参数:
A_prev - 来自上一层(或输入层)的激活,维度为(上一层的节点数量,示例数)
W - 权重矩阵,numpy数组,维度为(当前层的节点数量,前一层的大小)
b - 偏向量,numpy阵列,维度为(当前层的节点数量,1)
activation - 选择在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】
返回:
A - 激活函数的输出,也称为激活后的值
cache - 一个包含“linear_cache”和“activation_cache”的字典,我们需要存储它以有效地计算后向传递
"""
if activation == "sigmoid":
# Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
### START CODE HERE ### (≈ 2 lines of code)
Z,linear_cache=linear_forward(A_prev,W,b)
A,activation_cache=sigmoid(Z)
### END CODE HERE ###
elif activation == "relu":
# Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
### START CODE HERE ### (≈ 2 lines of code)
Z,linear_cache=linear_forward(A_prev,W,b)
A,activation_cache=relu(Z)
### END CODE HERE ###
assert (A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)
return A, cache
def L_model_forward(X,parameters):
"""
实现[LINEAR-> RELU] *(L-1) - > LINEAR-> SIGMOID计算前向传播,也就是多层网络的前向传播,为后面每一层都执行LINEAR和ACTIVATION
参数:
X - 数据,numpy数组,维度为(输入节点数量,示例数)
parameters - initialize_parameters_deep()的输出
返回:
AL - 最后的激活值
caches - 包含以下内容的缓存列表:
linear_relu_forward()的每个cache(有L-1个,索引为从0到L-2)
linear_sigmoid_forward()的cache(只有一个,索引为L-1)
"""
caches = []
A = X
L = len(parameters) // 2 # number of layers in the neural network
# Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
for l in range(1, L): #注意range是(1,L),最后的L不算进循环
A_prev = A
### START CODE HERE ### (≈ 2 lines of code)
A,cache=linear_activation_forward(A_prev,parameters['W' + str(l)], parameters['b' + str(l)], "relu")
caches.append(cache)
### END CODE HERE ###
# Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
### START CODE HERE ### (≈ 2 lines of code)
AL,cache=linear_activation_forward(A,parameters['W' + str(L)], parameters['b' + str(L)], "sigmoid")
caches.append(cache)
### END CODE HERE ###
assert(AL.shape == (1,X.shape[1]))
return AL, caches
def compute_cost(AL,Y):
"""
实施等式(4)定义的成本函数。
参数:
AL - 与标签预测相对应的概率向量,维度为(1,示例数量)
Y - 标签向量(例如:如果不是猫,则为0,如果是猫则为1),维度为(1,数量)
返回:
cost - 交叉熵成本
"""
m = Y.shape[1]
# Compute loss from aL and y.
### START CODE HERE ### (≈ 1 lines of code)
cost=np.sum(np.multiply(np.log(AL),Y) + np.multiply(np.log(1 - AL), 1 - Y))/(-m)
### END CODE HERE ###
cost = np.squeeze(cost) # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
assert(cost.shape == ())
return cost
def linear_backward(dZ,cache):
"""
为单层实现反向传播的线性部分(第L层)
参数:
dZ - 相对于(当前第l层的)线性输出的成本梯度
cache - 来自当前层前向传播的值的元组(A_prev,W,b)
返回:
dA_prev - 相对于激活(前一层l-1)的成本梯度,与A_prev维度相同
dW - 相对于W(当前层l)的成本梯度,与W的维度相同
db - 相对于b(当前层l)的成本梯度,与b维度相同
"""
A_prev, W, b = cache
m = A_prev.shape[1]
### START CODE HERE ### (≈ 3 lines of code)
dA_prev = np.dot(W.T, dZ)
dW=np.dot(dZ,A_prev.T)/m
db=np.sum(dZ,axis=1,keepdims=True)/m
### END CODE HERE ###
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db
def linear_activation_backward(dA,cache,activation="relu"):
"""
实现LINEAR-> ACTIVATION层的后向传播。
参数:
dA - 当前层l的激活后的梯度值
cache - 我们存储的用于有效计算反向传播的值的元组(值为linear_cache,activation_cache)
activation - 要在此层中使用的激活函数名,字符串类型,【"sigmoid" | "relu"】
返回:
dA_prev - 相对于激活(前一层l-1)的成本梯度值,与A_prev维度相同
dW - 相对于W(当前层l)的成本梯度值,与W的维度相同
db - 相对于b(当前层l)的成本梯度值,与b的维度相同
"""
linear_cache, activation_cache = cache
if activation == "relu":
### START CODE HERE ### (≈ 2 lines of code)
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
### END CODE HERE ###
elif activation == "sigmoid":
### START CODE HERE ### (≈ 2 lines of code)
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
### END CODE HERE ###
return dA_prev, dW, db
def L_model_backward(AL,Y,caches):
"""
对[LINEAR-> RELU] *(L-1) - > LINEAR - > SIGMOID组执行反向传播,就是多层网络的向后传播
参数:
AL - 概率向量,正向传播的输出(L_model_forward())
Y - 标签向量(例如:如果不是猫,则为0,如果是猫则为1),维度为(1,数量)
caches - 包含以下内容的cache列表:
linear_activation_forward("relu")的cache,不包含输出层
linear_activation_forward("sigmoid")的cache
返回:
grads - 具有梯度值的字典
grads [“dA”+ str(l)] = ...
grads [“dW”+ str(l)] = ...
grads [“db”+ str(l)] = ...
"""
grads = {}
L = len(caches) # the number of layers
m = AL.shape[1]
Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
# Initializing the backpropagation
### START CODE HERE ### (1 line of code)
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
### END CODE HERE ###
# Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "AL, Y, caches". Outputs: "grads["dAL"], grads["dWL"], grads["dbL"]
### START CODE HERE ### (approx. 2 lines)
current_cache = caches[L-1]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, "sigmoid")
### END CODE HERE ###
for l in reversed(range(L-1)):
# lth layer: (RELU -> LINEAR) gradients.
# Inputs: "grads["dA" + str(l + 2)], caches". Outputs: "grads["dA" + str(l + 1)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)]
### START CODE HERE ### (approx. 5 lines)
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l+2)], current_cache, activation = "relu") # l+2=L
grads["dA" + str(l + 1)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
### END CODE HERE ###
return grads
def update_parameters(parameters, grads, learning_rate):
"""
使用梯度下降更新参数
参数:
parameters - 包含你的参数的字典
grads - 包含梯度值的字典,是L_model_backward的输出
返回:
parameters - 包含更新参数的字典
参数[“W”+ str(l)] = ...
参数[“b”+ str(l)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural network
# Update rule for each parameter. Use a for loop.
### START CODE HERE ### (≈ 3 lines of code)
for l in range(L):
parameters['W'+str(l+1)]-=(learning_rate*(grads['dW'+str(l+1)]))
parameters['b'+str(l+1)]-=(learning_rate*(grads['db'+str(l+1)]))
### END CODE HERE ###
return parameters
def two_layer_model(X,Y,layers_dims,learning_rate=0.0075,num_iterations=3000,print_cost=False,isPlot=True):
"""
实现一个两层的神经网络,【LINEAR->RELU】 -> 【LINEAR->SIGMOID】
参数:
X - 输入的数据,维度为(n_x,例子数)
Y - 标签,向量,0为非猫,1为猫,维度为(1,数量)
layers_dims - 层数的向量,维度为(n_y,n_h,n_y)
learning_rate - 学习率
num_iterations - 迭代的次数
print_cost - 是否打印成本值,每100次打印一次
isPlot - 是否绘制出误差值的图谱
返回:
parameters - 一个包含W1,b1,W2,b2的字典变量
"""
np.random.seed(1)
grads={}
costs=[]
m=X.shape[1]
(n_x, n_h, n_y) = layers_dims
# Initialize parameters dictionary, by calling one of the functions you'd previously implemented
### START CODE HERE ### (≈ 1 line of code)
parameters=initialize_parameters(n_x,n_h,n_y)
### END CODE HERE ###
# Get W1, b1, W2 and b2 from the dictionary parameters.
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> SIGMOID. Inputs: "X, W1, b1". Output: "A1, cache1, A2, cache2".
### START CODE HERE ### (≈ 2 lines of code)
A1,cache1=linear_activation_forward(X,W1,b1,'relu')
A2,cache2=linear_activation_forward(A1,W2,b2,'sigmoid')
### END CODE HERE ###
# Compute cost
### START CODE HERE ### (≈ 1 line of code)
cost=compute_cost(A2,Y)
### END CODE HERE ###
# Initializing backward propagation
dA2=(-Y/A2)+(1-Y)/(1-A2)
# Backward propagation. Inputs: "dA2, cache2, cache1". Outputs: "dA1, dW2, db2; also dA0 (not used), dW1, db1".
### START CODE HERE ### (≈ 2 lines of code)
dA1, dW2, db2=linear_activation_backward(dA2,cache2,activation="sigmoid")
dA0, dW1, db1=linear_activation_backward(dA1,cache1,activation="relu")
### END CODE HERE ###
# Set grads['dWl'] to dW1, grads['db1'] to db1, grads['dW2'] to dW2, grads['db2'] to db2
grads['dW1'] = dW1
grads['db1'] = db1
grads['dW2'] = dW2
grads['db2'] = db2
# Update parameters.
### START CODE HERE ### (approx. 1 line of code)
parameters=update_parameters(parameters, grads, learning_rate)
### END CODE HERE ###
# Retrieve W1, b1, W2, b2 from parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# Print the cost every 100 training example
if print_cost and i % 100 == 0:
print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=True,isPlot=True):
"""
实现一个L层神经网络:[LINEAR-> RELU] *(L-1) - > LINEAR-> SIGMOID。
参数:
X - 输入的数据,维度为(n_x,例子数)
Y - 标签,向量,0为非猫,1为猫,维度为(1,数量)
layers_dims - 层数的向量,维度为(n_y,n_h,···,n_h,n_y)
learning_rate - 学习率
num_iterations - 迭代的次数
print_cost - 是否打印成本值,每100次打印一次
isPlot - 是否绘制出误差值的图谱
返回:
parameters - 模型学习的参数。 然后他们可以用来预测。
"""
np.random.seed(1)
costs = [] # keep track of cost
# Parameters initialization.
### START CODE HERE ###
parameters=initialize_parameters_deep(layers_dims)
### END CODE HERE ###
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: [LINEAR -> RELU]*(L-1) -> LINEAR -> SIGMOID.
### START CODE HERE ### (≈ 1 line of code)
AL, caches=L_model_forward(X,parameters)
### END CODE HERE ###
# Compute cost.
### START CODE HERE ### (≈ 1 line of code)
cost=compute_cost(AL,Y)
### END CODE HERE ###
# Backward propagation.
### START CODE HERE ### (≈ 1 line of code)
grads= L_model_backward(AL,Y,caches)
### END CODE HERE ###
# Update parameters.
### START CODE HERE ### (≈ 1 line of code)
parameters=update_parameters(parameters, grads, learning_rate)
### END CODE HERE ###
# Print the cost every 100 training example
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
if (isPlot==True):
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
def predict(X, y, parameters):
"""
该函数用于预测L层神经网络的结果,当然也包含两层
参数:
X - 测试集
y - 标签
parameters - 训练模型的参数
返回:
p - 给定数据集X的预测
"""
m = X.shape[1]
n = len(parameters) // 2 # 神经网络的层数
p = np.zeros((1,m))
#根据参数前向传播
probas, caches = L_model_forward(X, parameters)
for i in range(0, probas.shape[1]):
if probas[0,i] > 0.5:
p[0,i] = 1
else:
p[0,i] = 0
print("准确度为: " + str(float(np.sum((p == y))/m)))
return p
def print_mislabeled_images(classes, X, y, p):
"""
绘制预测和实际不同的图像。
X - 数据集
y - 实际的标签
p - 预测
"""
a = p + y
mislabeled_indices = np.asarray(np.where(a == 1))
plt.rcParams['figure.figsize'] = (40.0, 40.0) # set default size of plots
num_images = len(mislabeled_indices[0])
for i in range(num_images):
index = mislabeled_indices[1][i]
plt.subplot(2, num_images, i + 1)
plt.imshow(X[:,index].reshape(64,64,3), interpolation='nearest')
plt.axis('off')
plt.title("Prediction: " + classes[int(p[0,index])].decode("utf-8") + " \n Class: " + classes[y[0,index]].decode("utf-8"))
train_set_x_orig , train_set_y , test_set_x_orig , test_set_y , classes = lr_utils.load_dataset()
train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
train_x = train_x_flatten / 255
train_y = train_set_y
test_x = test_x_flatten / 255
test_y = test_set_y
'''
n_x = 12288
n_h = 7
n_y = 1
layers_dims = (n_x,n_h,n_y)
parameters = two_layer_model(train_x, train_set_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost=True,isPlot=True)
'''
layers_dims = [12288, 20, 20, 120, 1] # 5-layer model
parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True,isPlot=True)
predictions_train = predict(train_x, train_y, parameters) #训练集
predictions_test = predict(test_x, test_y, parameters) #测试集
#print_mislabeled_images(classes, test_x, test_y, predictions_test)
## START CODE HERE ##
my_image = "6CE5104F8B4F5AEAD07122456EF517A3.jpg" # change this to the name of your image file
my_label_y = [1] # the true class of your image (1 -> cat, 0 -> non-cat)
## END CODE HERE ##
num_px=64
fname = "images/" + my_image
image = np.array(plt.imread(fname))
my_image = resize(image, (num_px,num_px)).reshape((num_px*num_px*3,1))
my_predicted_image = predict(my_image, my_label_y, parameters)
plt.imshow(image)
print ("y = " + str(np.squeeze(my_predicted_image)) + ", your L-layer model predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") + "\" picture.")
此处要注意深度神经网络的初始化不是随机矩阵×0.001,不然代价函数J会卡在一个数左右降低十分缓慢。激活函数输出值接近于0会导致梯度非常接近于0,因此会导致梯度消失。解决方法在第二课优化中提到
6.步骤总结
《1》初始化网络参数
《2》前向传播
2.1 计算一层的中线性求和的部分
2.2 计算激活函数的部分(ReLU使用L-1次,Sigmod使用1次)
2.3 结合线性求和与激活函数
《3》计算误差
《4》反向传播
4.1 线性部分的反向传播公式
4.2 激活函数部分的反向传播公式
4.3 结合线性部分与激活函数的反向传播公式
《5》更新参数