史上最直白的ICA教程之一

前言

独立成分分析ICA是一个在多领域被应用的基础算法。ICA是一个不定问题，没有确定解，所以存在各种不同先验假定下的求解算法。相比其他技术，ICA的开源代码不是很多，且存在黑魔法–有些步骤并没有在论文里提到，但没有这些步骤是无法得到正确结果的。

本文给出一个ICA最大似然解法的推导，以及FastICA的python实现，限于时间和实际需求，没有对黑魔法部分完全解读，只保证FastICA实现能得到正确结果。

有兴趣的童鞋可以在未来补上相关内容。

ICA问题表述

设 X 是随机向量，且 X∈Rn×1 ，这也就说， X 里有 n 个成员，每个成员是一个随机变量：

X=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜x1x2...xi...xn⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟

其中，  xi 是一个随机变量。

随机变量有诸多特性，殆由概率论和数理统计教科书详述备尽，在此不一一叙述。

X 里的 n 个随机变量是相互非独立的，在一定的假设下，可以用 n 个相互独立的随机变量线性组合重新表达 X ，也就是说：

⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜x1x2...xi...xn⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟=A⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜s1s2...si...sn⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟

其中， si 是一个随机变量，且两两相互独立， A 是满秩矩阵，且 A∈Rn×n 。
令:

S=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜s1s2...si...sn⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟

则：

X=AS

又有:

S=A−1X

令：

W=A−1

则:

S=WX

其中， W∈Rn×n 。

记录随机向量 X 的值 m 次，则形成数据集：

D=⎛⎝⎜⎜⎜⎜d1,1d2,1...dn,1d1,2d2,2...dn,2............d1,md2,m...dn,m⎞⎠⎟⎟⎟⎟

其中， D∈Rn×m

ICA的目标，就是在只知道 D 的情况下，估算 A ， W ， S 的值。

实例：在一个大厅里，有 n 个人在随机聊天。在大厅的不同角落，布置 n 个麦克风记录大厅的声音，每秒一个记录，一共记录m秒。麦克风记录的混合声音，多个麦克风记录不同位置的混合声音。ICA的目标，就是从混声录音中将每个人的声音分离出来。

理论推导

由前可知:

 si=(wi,1wi,2...wi,j...wi,n)⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜x1x2...xi...xn⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟

令:

wi=(wi,1wi,2...wi,j...wi,n)

则:

si=wiX

设随机变量 si 概率密度函数是 psi(si) ，其中 p 的右下角 si 表示随机变量标示，括号中的 si 表示自变量。

由于 S 的 n 个成员 si 是相互独立的，所以 S 的概率密度函数为:

pS(s)=∏i=1npsi(si)

设 X 的概率密度函数是 pX(x) ，如何根据 si 的概率密度函数求 pX(x) 呢？这是可以做到的。

设随机向量 X 的概率分布函数是 FX(x) ，根据概率分布函数和概率密度函数的关系可知：

pX(x)=F′X(x)

同理，设随机向量 S 的概率分布函数是 FS(s) ，则：

pS(s)=F′S(s)

根据概率分布函数的定义，有:

FX(x)=P(X<x)

FS(s)=P(S<s)

那么：

pX(x)=F′X(x)=(P(X<x))′=(P(U<u))′=(P(U<s))′=(∥P(U<Wx)∥)′=(∥P(S<Wx)∥)′=(∥FS(Wx)∥)′=∥F′S(Wx)∥=∥pS(Wx)(Wx)′∥=∥pS(Wx)W∥=pS(Wx)∥W∥=∥W∥∏i=1npsi(wix)

其中，上式的第2个等号是概率密度函数的定义，第3个等号是做变量等价代换，以免直接从X变换到S导致思维混乱，第4个等号到第6个等号是逐步将X代换到S，第7个等号是回到 S 的概率分布函数定义，第8个等号到第10个等号是求导。

从第5个等号开始，对整个等式取行列式运算，因为 pX(x) 一定是标量，对标量做行列式运算是它自身。那么，到了第10个等号，又因为 pS(WX) 一定是标量，所以可以从行列式运算拿到外面。这里避免的问题的是，如果不对整个等式取行列式，得到的结果是矩阵 W 而不是 ∥W∥ ，这是没有道理的。

注意，在上式中， x 是一个向量，且 x∈Rn×1 ， wi∈R1×n ， psi(si) 是一个单自变量的函数， pX(x) 是一个多自变量函数，它的自变量是 x 里的多个变量，这样等式左右的每一步就清晰了。

下一步是根据数据集计算 W 的值，从概率的角度来说，如果数据集已经记录，那么让这个数据集出现概率最大的 W 就是最优值。

前述数据集出现的概率是:

L=∏i=1m(∥W∥∏j=1npsj(wjdi))

其中， ∏ 表示连乘， di 是 D 的第 i 列，也就是：

di=⎛⎝⎜⎜⎜⎜di,1di,2...di,n⎞⎠⎟⎟⎟⎟

di 的物理意义，也就是第 i 次记录随机向量 X 得到的 n 个值，这 n 个值分别对应 n 个 xi 随机变量。注意，不要把 di 和 xi 混淆，前者表示 D 的一列数据，后者是粗体表示一个随机变量。

上式有最大值，当它取最大值时候的 W 就是最优解。如果以梯度下降法求解，需要计算它对 W 的偏导，直接求偏导比较复杂，故对它两端取自然对数，则:

lnL=∑i=1m(ln∥W∥+∑j=1n(lnpsj(wjdi)))=∑i=1m∑j=1nlnpsj(wjdi)+mln∥W∥

当上式取最大值的时候， L 也同时取最大值，所以求 L 的最大值等价于求上式的最大值。

用梯度下降法求解上式，需要计算 ∂lnL∂W 。这是一个复杂的过程，先从计算 ∂L∂wu,v 开始，它表示 W 的第 u 行第 v 列的一个成员：

∂lnL∂wu,v=∑i=1m∑j=1n1psj(wjdi)∂psj(wjdi)∂wu,v+m∥W∥∂∥W∥∂wu,v=∑i=1m∑j=1n1psj(wjdi)∂psj(wjdi)∂wu,v+m∥W∥(−1)u+vMuv=∑i=1m1psu(wudi)∂psu(wudi)∂wu,v+m∥W∥(−1)u+vMuv

其中， (−1)u+vMuv 是 wu,v 的代数余子式， ∂psu(wuxi)∂wu,v 的值要根据 psi(si) 的具体形式求解。

对于 psi(si) ，如果在没有任何先验信息的情况下，是无法求解的。如果要求解上式，需要对它做一定的假设，在合理的假设下，可以达到相当不错的近似结果。

设随机变量 xi 的概率分布函数是sigmoid函数，因为它是递增，可微，且最大值不超过1，也就是说：

Fsi(si)=11+e−si

那么，概率密度函数就是:

psi(si)=F′si(si)=esi(1+esi)2

所以有：

psu(wudi)=ewudi(1+ewudi)2=ewudi(1+ewudi)−2

故:

∂psu(wudi)∂wu,v=ewudidi,v(1+ewudi)−2−2ewudi(1+ewudi)−3ewudidi,v=di,vewudi(1+ewudi)2(1−2ewudi1+ewudi)=di,vpsu(wudi)1−ewudi1+ewudi

其中， di,v 是 di 的第 v 行的一个成员。

因此:

∂lnL∂wu,v=∑i=1m1psu(wudi)∂psu(wudi)∂wu,v+m∥W∥(−1)u+vMuv=∑i=1m1psu(wudi)di,vpsu(wudi)1−ewudi1+ewudi+m∥W∥(−1)u+vMuv=∑i=1mdi,v1−ewudi1+ewudi+m∥W∥(−1)u+vMuv

现在对上式进行矩阵化，
令：

K=WD

其中， K∈Rn×m ， W∈Rn×n ， D∈Rn×m ，那么， ku,i 就是 K 的第 u 行的第 i 列的一个成员，
令：

g(x)=1−ex1+ex

令:

Z=g(K)=⎛⎝⎜⎜⎜⎜g(k1,1)g(k2,1)...g(kn,1)g(k1,2)g(k2,2)g(kn,2).........g(k1,m)g(k2,m)g(kn,m)⎞⎠⎟⎟⎟⎟

那么，就得到:

∂lnL∂wu,v=zTudv+m∥W∥(−1)u+vMuv

其中， zu 是 Z 的第 u 行， dv 是 D 的第 v 列。

于是，对 W 而言，则有：

∂lnL∂W=ZTD+m∥W∥(W∗)T

其中， W∗ 是 W 的伴随矩阵， (W∗)T 是 W∗ 的转置，它的第 i 行第 j 列的元素是 wi,j 的代数余子式，也就是 (−1)i+jMi,j 。

根据矩阵和它的伴随阵的性质可知:

WW∗=∥W∥I

其中， I 是单位矩阵。
根据上两式可知:

∂lnL∂W=ZTD+m∥W∥(W∗)T=ZTD+m∥W∥(∥W∥W−1)T=ZTD+m(W−1)T

那么，在梯度下降法求解 W 的时候，更新公式是:

W=W+α(ZTD+m(W−1)T)

其中， α 是学习速率。

最后的结论简洁且美，Verweile doch, du bist so schön。然并卵，按照这个结果实现代码，计算结果是不合理的，无法恢复原始信号。于是，在实现FastICA之后，可以认为本推导缺少一些黑魔法，至于到底缺少什么并不知道，限于时间关系和实际需求，不再继续研究下去。

FastICA

FastICA计算性能更好。《Indepdent Componet analysis》一书在第8章给出了FastICA的算法流程，如下:

白化

FastICA需要对数据做白化处理。设 x 是一个随机变量，存在一个线性变换 V 将它变换成 z ：

z=Vx

且：

E{zzT}=I

那么， V 就是白化变换矩阵。

x 的协方差阵是 Cx=E{xxT} ， Cx=PDPT ， P 是 Cx 的单位特征向量， D 是 Cx 的特征值组成的对角阵。那么， V 的值就是：

V=D−12PT

证明如下：
根据相关性质，有 PT=P−1 ，由于 D 对角阵，则 (D−12)T=D−12 ，
那么：

E{Vx(Vx)T}=E{VxxTVT}=E{VPDPTVT}=E{VPDPTVT}=E{D−12PTPDPTP(D−12)T}=E{D−12DD−12}=E{I}=I

代码实现

基于python2.7，matplotlib，numpy实现ICA，主要参考sklean的FastICA实现。

#!/usr/bin/env python

#FastICA from ICA book, table 8.4 

import math
import random
import matplotlib.pyplot as plt
from numpy import *

n_components = 2

def f1(x, period = 4):
    return 0.5*(x-math.floor(x/period)*period)

def create_data():
    #data number
    n = 500
    #data time
    T = [0.1*xi for xi in range(0, n)]
    #source
    S = array([[sin(xi)  for xi in T], [f1(xi) for xi in T]], float32)
    #mix matrix
    A = array([[0.8, 0.2], [-0.3, -0.7]], float32)
    return T, S, dot(A, S)

def whiten(X):
    #zero mean
    X_mean = X.mean(axis=-1)
    X -= X_mean[:, newaxis]
    #whiten
    A = dot(X, X.transpose())
    D , E = linalg.eig(A)
    D2 = linalg.inv(array([[D[0], 0.0], [0.0, D[1]]], float32))
    D2[0,0] = sqrt(D2[0,0]); D2[1,1] = sqrt(D2[1,1])
    V = dot(D2, E.transpose())
    return dot(V, X), V

def _logcosh(x, fun_args=None, alpha = 1):
    gx = tanh(alpha * x, x); g_x = gx ** 2; g_x -= 1.; g_x *= -alpha
    return gx, g_x.mean(axis=-1)

def do_decorrelation(W):
    #black magic
    s, u = linalg.eigh(dot(W, W.T))
    return dot(dot(u * (1. / sqrt(s)), u.T), W)

def do_fastica(X):
    n, m = X.shape; p = float(m); g = _logcosh
    #black magic
    X *= sqrt(X.shape[1])
    #create w
    W = ones((n,n), float32)
    for i in range(n): 
        for j in range(i):
            W[i,j] = random.random()

    #compute W
    maxIter = 200
    for ii in range(maxIter):
        gwtx, g_wtx = g(dot(W, X))
        W1 = do_decorrelation(dot(gwtx, X.T) / p - g_wtx[:, newaxis] * W)
        lim = max( abs(abs(diag(dot(W1, W.T))) - 1) )
        W = W1
        if lim < 0.0001:
            break
    return W

def show_data(T, S):
    plt.plot(T, [S[0,i] for i in range(S.shape[1])], marker="*")
    plt.plot(T, [S[1,i] for i in range(S.shape[1])], marker="o")
    plt.show()

def main():
    T, S, D = create_data()
    Dwhiten, K = whiten(D)
    W = do_fastica(Dwhiten)
    #Sr: reconstructed source
    Sr = dot(dot(W, K), D)
    show_data(T, D)
    show_data(T, S)
    show_data(T, Sr)

if __name__ == "__main__":
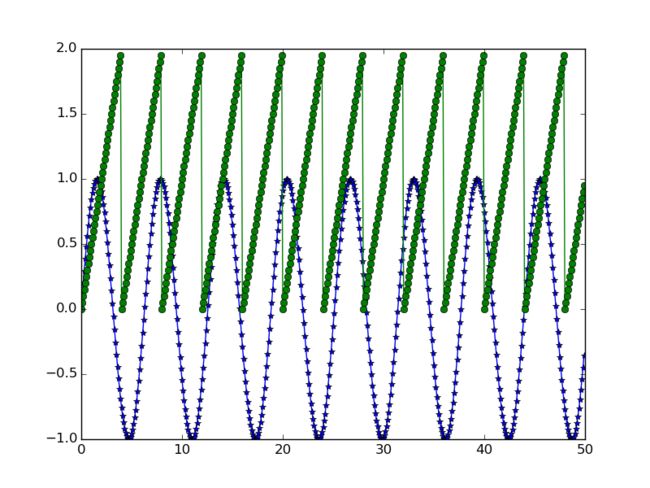
    main()    

在这个实现中，创建了两个数据源，一个是正弦函数，一个是线性周期函数，它们的图形如下：

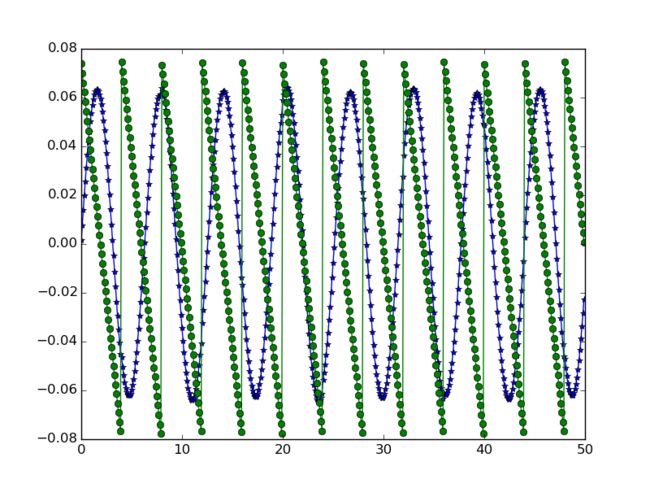
将这两个数据源混合成两个新数据源，也就是“可观测”的数据，它们的图像如下：

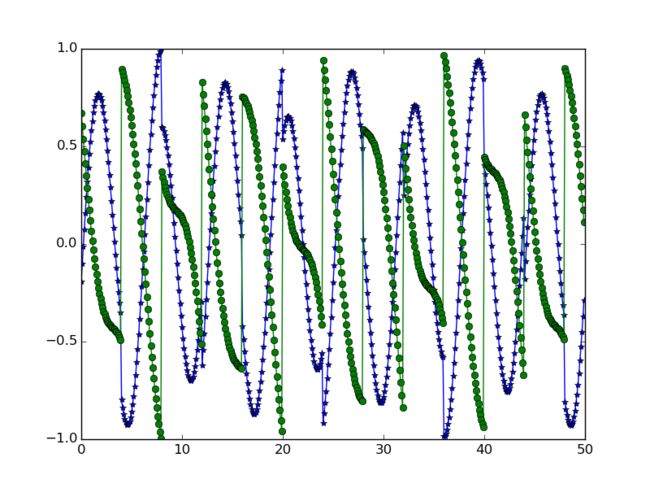
经过FastICA处理后，重建数据源。注意，此时的数据源在图形形状上跟初始数据源具有相似性，但幅度是不一样的，且可能会发生翻转，这是因为ICA是一个不定问题，有多个解符合假设，不是唯一解。