Elman神经网络与自适应共振网络（ART）

这几天在回过头看一些比较基础的东西，发现了两个早期研究的神经网络，Elman与ART网络，类似于上世纪80年代的hopfield神经网络，BM/RBM/DBN，RBF，SOM，以及同时期的SVM算法等等，虽然那个时候可能比较冷门，并且处于神经网络偏底层研究，与生物学结合很密切，但是想法还是很不错的。

Elman神经网络介绍以及Matlab实现

Elman神经网络介绍

1.特点
Elman神经网络是一种典型的动态递归神经网络，它是在BP网络基本结构的基础上，在隐含层增加一个承接层，作为一步延时算子，达到记忆的目的，从而使系统具有适应时变特性的能力，增强了网络的全局稳定性，它比前馈型神经网络具有更强的计算能力，还可以用来解决快速寻优问题。
2.结构
Elman神经网络是应用较为广泛的一种典型的反馈型神经网络模型。一般分为四层：输入层、隐层、承接层和输出层。其输入层、隐层和输出层的连接类似于前馈网络。输入层的单元仅起到信号传输作用，输出层单元起到加权作用。隐层单元有线性和非线性两类激励函数，通常激励函数取Signmoid非线性函数。而承接层则用来记忆隐层单元前一时刻的输出值，可以认为是一个有一步迟延的延时算子。隐层的输出通过承接层的延迟与存储，自联到隐层的输入，这种自联方式使其对历史数据具有敏感性，内部反馈网络的加入增加了网络本身处理动态信息的能力，从而达到动态建模的目的。其结构图如下图所示。

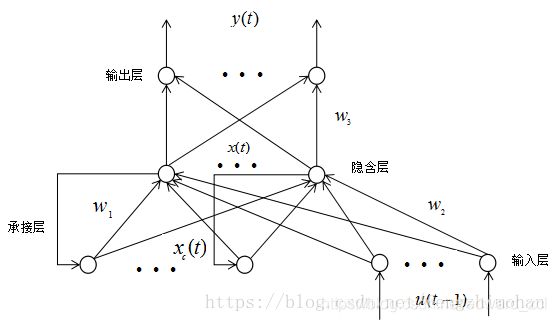
其网络的数学表达式为：

其中，y为m维输出节点向量；x为n维中间层节点单元向量；u为r维输入向量；xc为n维反馈状态向量；w3为中间层到输出层连接权值；w2为输入层到中间层连接权值；w1为承接层到中间层连接权值；g()为输出神经元的传递函数，是中间层输出的线性组合；f()为中间层神经元的传递函数，常采用S函数。
3.与BP网络的区别
它是动态反馈型网络，它能够内部反馈、存储和利用过去时刻输出信息，既可以实现静态系统的建模，还能实现动态系统的映射并直接反应系统的动态特性，在计算能力及网络稳定性方面都比BP神经网络更胜一筹。
4.缺点
与BP神经网络一样，算法都是采用基于梯度下降法，会出现训练速度慢和容易陷入局部极小点的缺点，对神经网络的训练较难达到全局最优。

基于Matlab实现Elman神经网络

在MATLAB中，Elman神经网络可以通过调用newelm()实现。

例子：利用Elman神经网络实现MATLAB的数据预测。

%输入数据  
P=[3.2 3.2 3 3.2 3.2 3.4 3.2 3 3.2 3.2;
9.6 10.3 9 10.3 10.1 10 9.6 9 9.6 9.2;
3.45 3.75 3.5 3.65 3.5 3.4 3.55 3.5 3.55 3.5;
2.15 2.2 2.2 2.2 2 2.15 2.14 2.1 2.1 2.1;
140 120 140 150 80 130 130 100 130 140;
2.8 3.4 3.5 2.8 1.5 3.2 3.5 1.8 3.5 2.5;
11 10.9 11.4 10.8 11.3 11.5 11.8 11.3 11.8 11;
50 70 50 80 50 60 65 40 65 50 ];  %训练数据
T=[2.24 2.33 2.24 2.32 2.2 2.27 2.2 2.26 2.2 2.24];%训练输出实际值
TestInput=[3.2 3.9 3.1 3.2 3.0;
9.5 9 9.5 9.7 9.3;
3.4 3.1 3.6 3.45 3.3;
2.15 2 2.1 2.15 2.05;
115 80 90 130 100;
2.8 2.2 2.7 2.6 2.8;
11.9 13 11.1 10.85 11.2;
50 50 70 70 50];%测试数据
TestOutput=[2.24 2.2 2.2 2.35 2.2]; %测试输出实际值

[pn,minp,maxp,tn,mint,maxt]=premnmx(P,T);
p2= tramnmx(TestInput,minp,maxp);
%创建Elman神经网络  
net_1 = newelm(minmax(pn),[8,1],{'tansig','purelin'},'traingdm');  
  
%设置训练参数  
net_1.trainParam.show = 50;  
net_1.trainParam.lr = 0.01;  
net_1.trainParam.mc = 0.9;  
net_1.trainParam.epochs =10000;  
net_1.trainParam.goal = 1e-3;  
net=init(net_1);%初始化网络  
%训练网络  
net = train(net,pn,tn);  
%使用训练好的网络，自定义输入  
PN = sim(net,p2); 
TestResult= postmnmx(PN,mint,maxt);%仿真值反归一化
%理想输出与训练输出的结果进行比较  
E =TestOutput - TestResult 
%计算误差  
MSE=mse(E);%计算均方误差  
figure(1)
plot(TestOutput,'bo-');
hold on;
plot(TestResult,'r*--');
legend('真实值','预测值');
save('Elman.mat','net');

运行结果如下：

（）多么原始的matlab神经网络工具箱啊。。）

误差结果为：
E =[0.48% 0.40% 0.12% 9.47% 2.28%]
平均误差为：2.55%

转载请标明出处，谢谢！。

如果感觉本文对您有帮助，请留下您的赞，您的支持是我坚持写作最大的动力，谢谢！

---

自适应共振网络（ART）应用研究

人类智能的特性之一是能在不忘记以前学习过的事物的基础上继续学习新事物。这项特性是目前多数类神经网络模型所欠缺的，这些类神经网络模型(例如反向传播类神经网络)一般都需要事先准备好的训练模式集进行训练。当训练完毕之后，神经元之间的连接强度就确定了，除非再有新的训练动作发生，否则这些连接强度不会再有任何改变。当有新模式出现时，这些类神经网络模型只能由用户将新模式加到训练模式中，形成新的训练模式集，然后重新训练所有神经元间的连接强度，也就是旧有的知识必须重新训练一遍。这些类神经网络模型，只有记忆而没有智能，没有辨识新事件出现的能力，也没有自我学习扩充记忆的能力。

为了试图解决这些问题，Grossberg等人模仿人的视觉与记忆的交互运作，提出所谓自适应共振理论(Adaptive Resonance Theory,ART)。他多年来一直试图为人类的心理和认知活动建立统一的数学理论，ART就是这一理论的核心部分。随后G.A.Carpenter又与S.Grossberg提出了ART网络。

ART是一种自组织神经网络结构，是无教师的学习网络。当在神经网络和环境有交互作用时， 对环境信息的编码会自发地在神经网中产生， 则认为神经网络在进行自组织活动。ART不像其它类神经网络模型，分为训练阶段及测试阶段，需事先准备好训练模式集及测试模式集。ART时时处在训练状态及测试状态。当它开始工作的时候可以不用确定到底需要多少个神经元，先给几个就行，或者根本不用给它。ART的学习就像小孩成长一样，头脑也会同步长大。当 ART发现记忆的神经元不够用时，会动态长出新的神经元去记忆新模式，形成新聚类，而不会影响到己经存在的神经元间的连接，因此 ART 可以在不忘掉先前学习过的事物的情况下，继续学习新事物。

目前，ART 有很多版本：ART1是最早的版本，由 Carpenter 和 Grossberg 于1987 年提出，ART1 含有并行架构的主-从式算法（leader-followeralgorithm），在算法的激活及匹配函数中运用了集合运算，主要处理只含 0 与 1 的影像（即黑白）识别问题。ART2可以处理灰度（即模拟值）输入ART3具有多级搜索架构，它融合了前两种结构的功能并将两层神经网络扩展为任意多层的神经元网络。由于ART3 在神经元的运行模型中纳入了神经元的生物电化学反应机制，因而其功能和能力得到了进一步扩展。

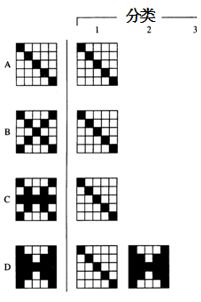
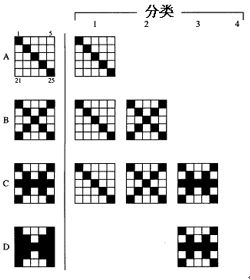
  在此我将结合实验和大家分享学习ART1模型的基本原理和学习算法。为了进一步了解ART1网络，于是设计一组实验，按照M=4，N=25设计网络，如下图A、B、C、D所示。按照顺序输入A、B、C、D后，得出如图所示的四幅黑白点阵图，通过改变不同的警戒阈值ρ，我们会得出怎样的分类呢？

一、问题分析

为了对四幅黑白点阵图的进行模式识别，本实验在运用ART1模型理论的基础上，将警戒阈值ρ设置为0.7和0.3两个值，分别得到不同的实验结果。这样就对ART1网络的学习过程进行了验证。

1、ART模型基本原理

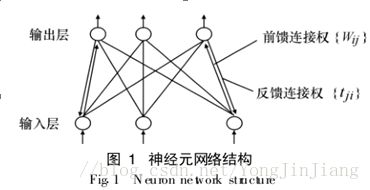
人工神经网络具有存储和应用经验知识的自然特性。神经网络具有很强的鲁棒性，即使系统连接线被破坏了多达50%，它仍能以优化工作状态来处理信息。自适应共振理论（ART）借鉴人的认知过程和大脑工作的特点，是一种模仿人脑认知过程的自组织聚类算法。在解决大量数据聚类和分类时，聚类效果好且稳定,此外还能高效利用系统的记忆资源。本次实验参考相关文献，以ART网络中的ART1模型为理论基础来实现字符识别。这种网络（图1）的输入层和输出层之间为双向连接，反馈连接权{ t ji }记忆已学的输入模式。

ART1人工神经网络由两层神经元组成，分别称为比较层（输入层）和识别层（输出层）。类别判断是由在识别层中的一个单一神经元来作出的，类似于大脑皮层感受区中的细胞组，比较层中的神经元对模式的输入特性做出响应。在这两层之间的突触连接（权值）可以根据两种不同的学习规则进行双向修改。识别层的神经元具有允许竞争的抑制连接。该网络结构还包括三个附加模块，即增益1、增益2和复位模块，如下图：

ART1人工神经网络的子系统包括两层具有前馈和后馈特征的神经元（比较层和识别层）。该系统决定输入数据是否与已存储的一个原型相匹配，如果匹配，就会产生共振。监视子系统负责监测在识别层自下而上和自上而下模式之间的失配情况。识别层对输入矢量所做出的反应，可以比作是通过警戒机制的原始输入矢量。警戒提供了一种输入矢量与激励识别层神经元相应的聚类中心之间的距离测度。当警戒低于预先设置的门限值时，必须创建一个新的类别并将输入矢量存于该类别中。就是说，在识别层，将先前未分配的神经元分配到一个与新的输入模式相联系的新类别中。识别层遵循胜者取全部的原理，如果输入的数据通过了警戒，获胜的神经元（与输入数据最为匹配的一个神经元）就会被训练，以便他在特性空间中相应的聚类中心移向输入数据模式。

二、解决方案

1、算法设计

（1）初始化

由于前向连接权{W ij}在网络学习时，负担着对学习模式的记忆功能，为给所有的学习模式提供平等竞争的机会，{Wij}的初值全部设置为1 /(1+n)，其中n为输入层单元数。反馈连接权{t ji}最终将记忆已经学过的输入模式，其值最终为0和1二值的形式，为在开始时不丢失信息，可设{ t ji }=1。ART1网络有一个特殊的参数，即警戒参数ρ，按需要设定为0<ρ< 1。为了实验顺利进行，我们在初始化中设定警戒门限p= 0.3。

（2）样本输入并计算最大Sj

依次将4个输入模式样本读取到网络的输入层矩阵，提供给网络学习。在初始状态下，所有的{Wij}都相等，故所有的Sj都相同。无论初次学习还是以后增添样本，在计算Sj时都可能产生相同的Sj。这里程序设计为选择首次出现的Sj为获胜单元，作为本次学习样本的输出单元。

（3）反馈比较

选用最终的最大Sj为输入激活值最大的神经元，但该神经元能否代表输入模式的正确分类，还要将该输入模式与所对应的反馈连接权Tj=[ t j1 , t j2 , … , t jm ]比较，如果相等，则认为本次输入与网络产生了共振，网络不用再寻找。否则，将该神经元排除在下次识别范围之外，重复寻找最大Sj。所谓共振并不一定要求输入与反馈完全相等，允许的误差由警戒参数ρ确定。

2、编程实验

在对问题和算法进一步理解的基础上，本实验程序用python编写。首先建立N=25，M=4的网络，代码实现如下：

   N = 25
   M = 4
   VIGILANCE = 0.3
   PATTERN_ARRAY = [[1, 0, 0, 0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,1],
                                 [1, 0, 0, 0,1,0,1,0,1,0,0,0,1,0,0,0,1,0,1,0,1,0,0,0,1],
                                 [1, 0, 0, 0,1,0,1,0,1,0,1,1,1,1,1,0,1,0,1,0,1,0,0,0,1],
                                 [1, 0, 0, 0,1,1,1,0,1,1,1,1,1,1,1,1,1,0,1,1,1,0,0,0,1]]

其次，本实验通过定义ART1函数将ART1模型算法写入其中，

   def ART1(self,trainingPattern, isTraining):
        inputSum = 0
        activationSum = 0
        f2Max = 0
        reset = True
        for i in range(self.mNumClusters):
            self.f2[i] = 0.0
        for i in range(self.mInputSize):
            self.f1a[i] =float(trainingPattern[i])
        inputSum = self.get_vector_sum(self.f1a)
        for i in range(self.mInputSize):
            self.f1b[i] = self.f1a[i]
        for i in range(self.mNumClusters):
            for j in range(self.mInputSize):
                self.f2[i] += self.bw[i][j]* float(self.f1a[j])
        reset = True
        while reset:
            f2Max = self.get_maximum(self.f2)
            if f2Max == -1:
                f2Max = self.mNumClusters
                self.f2.append(0.0)
                self.tw.append([1.0] * self.mInputSize)
                self.bw.append([1.0 / (1.0 + self.mInputSize)]* self.mInputSize)
                self.mNumClusters+=1
            for i in range(self.mInputSize):
                self.f1b[i] = self.f1a[i]* math.floor(self.tw[f2Max][i])
            activationSum = self.get_vector_sum(self.f1b)
            reset = self.test_for_reset(activationSum,inputSum, f2Max)
        if isTraining:
            self.update_weights(activationSum,f2Max)

        return f2Max

1、取警戒参数设r=0.7，初始权值b ij=1/(1+n)=1/26，t ij=1。输入样本X 1，将X 1作为第一个类，并使第一个神经元与之对应，此时t ij = X 1，输入样本X 2，此时没有与第一个神经元竞争的神经元，而且不满足D ≥ ρ，因此将看做新的模式，并使第二个神经元与之对应，此时t i2 = X 2；

2、输入样本X 3，此时第一个与第二个神经元竞争，第一个神经元获胜，但警戒值测试失败，将其排除在下一次竞争范围之外，第二个神经元因而获胜但警戒值测试仍然失败，将X 3作为新的模式，并使第三个神经元与之对应，此时t i3 = X 3；

3、输入样本X 4，此时第三个神经元竞争获胜，并且通过警戒值测试，故认为是第三个神经元所代表的类，t i3保持不变，到此，网络保存了三个类。

本实验得出如下实验结果：

当r=0.7时，网络中存在三种分类，

四、总结

自适应共振理论(ART) 是一种自组织神经网络结构，是无教师的学习网络。当在神经网络和环境有交互作用时，对环境信息的编码会自发地在神经网中产生，认为神经网络在进行自组织活动。同时了解到了ART与其它类神经网络模型的区别，即ART 可以在不忘掉先前学习过的事物的情况下，继续学习新事物。

为了进一步理解ART模型，我们通过选取一个简单的例子来具体阐述其应用。在警戒参数分别为0.3与0.7的条件下进行实验，并选取Python计算机语言对其实现，得出结论：警戒参数越大，分类越细；警戒参数越小，分类越粗。

在程序的运行过程中，相对比较顺利，但也得承认数据测试的局限性，如选取的样本较小，警戒参数选取的过于主观性，很多未知的问题还没有发现。本人现就职于甜橙金融，对人工神经网络研究仍有余热，同时文章中存在的不足和缺陷，希望在以后有机会与大家多沟通交流。

更多参考：

https://blog.csdn.net/App_12062011/article/details/53463372
https://blog.csdn.net/mr_wuliboy/article/details/80656122
https://blog.csdn.net/qq_42633819/article/details/82942561
https://blog.csdn.net/yongjinjiang/article/details/79644213
https://blog.csdn.net/fengzhimohan/article/details/80847979