可微神经计算机(Differentiable neural computer)的介绍

可微神经计算机的介绍

一、介绍

如今，人工神经网络已经在模式识别、序列学习和强化学习方面表现出色，但因为没有额外的存储机制，使得在表示变量和需要存储长时间数据的情况下，神经网络的能力被有所限制。本文将基于Deepmind于2016年发表在《自然》杂志上的文章，对文章中所提出的可微神经计算机(Differentiable neural computer)进行一定的介绍，并针对Deepmind开源在Github上的代码进行一定的分析。

可微神经计算机（之后简称DNC）的一个单元(cell)主要由一个控制器和一个存储器构成，如图所示：

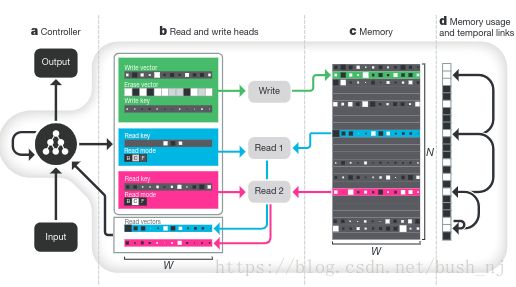
其中，控制器可以是人工神经网络，也可以是其他的机器学习模型；存储器可以理解为由读写头、内存单元和一些保存存储状态的单元组成。下面介绍控制器、存储器和两者之间的数据交互。

在介绍DNC单元之前，本节将补充一点我在实现代码过程中的一点经验。在构造一个复杂的变量之前，我们需要考虑该变量的以下几个方面：
变量类型(e.g. float32, int64)，
变量形状(e.g. [batch_size, time, length])，
变量范围(e.g. α∈[0,1] α ∈ [ 0 , 1 ] )，
变量之间关系(e.g. ∑ni=0αi⩽1 ∑ i = 0 n α i ⩽ 1 ) 。

二、控制器

论文上所用的控制器结构是一个变体的LSTM，在此简称 η η 。

在某一时刻 t ， η η 获得一个输入向量 xt∈ℝX x t ∈ R X 。另外，在t-1时刻，存储器从存储单元 Mt−1∈ℝN×W M t − 1 ∈ R N × W 中读取 R R 个向量: r1t−1,...,rRt−1 r t − 1 1 , . . . , r t − 1 R ，其中 rit−1∈ℝW r t − 1 i ∈ R W 。这样将向量 xt x t 与 R R 个读出的向量做连接(concatenate)操作，得控制器 η η 在t时刻的输入为

χt=[xt;r1t−1;...;rRt−1] χ t = [ x t ; r t − 1 1 ; . . . ; r t − 1 R ] 。
那么，对于有1个隐藏层的lstm网络（而论文中叙述的是一个多层lstm），隐藏层的输入门为：

it=σ(Wi[χt;ht−1]+bi) i t = σ ( W i [ χ t ; h t − 1 ] + b i ) ；
遗忘门为：
ft=σ(Wf[χt;ht−1]+bf) f t = σ ( W f [ χ t ; h t − 1 ] + b f ) ；
状态更新：
st=ftst−1+ittanh(Ws[χt;ht−1]+bs) s t = f t s t − 1 + i t t a n h ( W s [ χ t ; h t − 1 ] + b s ) ；
输出门为：
ot=σ(Wo[χt;ht−1]+bo) o t = σ ( W o [ χ t ; h t − 1 ] + b o ) ；
最后隐藏层输出：
ht=ottanh(st) h t = o t t a n h ( s t ) 。

论文要求，
在t时刻，控制网络 η η 需要产生输出向量 ϑt∈ℝY ϑ t ∈ R Y ，并产生控制信息向量 ξt∈ℝWR+3W+5R+3 ξ t ∈ R W R + 3 W + 5 R + 3 ，定义如下：

ϑt=Wϑht ϑ t = W ϑ h t ；
ξt=Wξht ξ t = W ξ h t 。

最后， η η 产生一个输出向量 yt∈ℝY y t ∈ R Y ，即目标向量 zt∈ℝY z t ∈ R Y 的预测向量（对于监督学习）， η η 的输出向量 yt y t 定义如下：

yt=ϑt+Wr[r1t;...;rRt] y t = ϑ t + W r [ r t 1 ; . . . ; r t R ]

三、控制信息向量

对控制信息向量 ξt∈ℝWR+3W+5R+3 ξ t ∈ R W R + 3 W + 5 R + 3 进行细分(subdivid)，得到如下控制信息：

ξt=[kr,1t;...;kr,Rt;βr,1t^;...;βr,Rt^;kwt;βwt^;et^;vt;f1t^;...;fRt^;gat^;gwt^;π1t^;...;πRt^] ξ t = [ k t r , 1 ; . . . ; k t r , R ; β t r , 1 ^ ; . . . ; β t r , R ^ ; k t w ; β t w ^ ; e t ^ ; v t ; f t 1 ^ ; . . . ; f t R ^ ; g t a ^ ; g t w ^ ; π t 1 ^ ; . . . ; π t R ^ ]

在介绍控制信息之前，本节需要引入一个变量空间 SN S N ，定义如下：

SN={α∈ℝN:α∈[0,1],∑Ni=1αi=1} S N = { α ∈ R N : α ∈ [ 0 , 1 ] , ∑ i = 1 N α i = 1 }

对于读写一块内存矩阵 M∈ℝN×W M ∈ R N × W ，存储器需要很多控制信息，论文要求有10种控制信息，这10种信息主要分两类：控制写与控制读，定义如下：

R read keys:

{kr,it∈ℝW;1⩽i⩽R} { k t r , i ∈ R W ; 1 ⩽ i ⩽ R }

R read strengths:

{βr,it=oneplus(βr,it^)∈[1,∞];1⩽i⩽R} { β t r , i = o n e p l u s ( β t r , i ^ ) ∈ [ 1 , ∞ ] ; 1 ⩽ i ⩽ R }

R free gates:

{fit=σ(fit^)∈[0,1];1⩽i⩽R} { f t i = σ ( f t i ^ ) ∈ [ 0 , 1 ] ; 1 ⩽ i ⩽ R }

R read modes:

{πit=softmax(πit^)∈S3;1⩽i⩽R} { π t i = s o f t m a x ( π t i ^ ) ∈ S 3 ; 1 ⩽ i ⩽ R }

the write key:

kwt∈ℝW k t w ∈ R W

the write strength:

βwt=oneplus(βw^)∈[1,∞] β t w = o n e p l u s ( β w ^ ) ∈ [ 1 , ∞ ]

the erase vector:

et=σ(et^)∈[0,1]W e t = σ ( e t ^ ) ∈ [ 0 , 1 ] W

the write vector:

vt∈ℝW v t ∈ R W

the allocation gate:

gat=σ(gat^)∈[0,1] g t a = σ ( g t a ^ ) ∈ [ 0 , 1 ]

the write gate:

gwt=σ(gwt^)∈[0,1] g t w = σ ( g t w ^ ) ∈ [ 0 , 1 ]

对于上述控制信息的使用，将在下面的部分介绍。

四、存储器读写机制

论文规定，DNC单元在将向量写入内存矩阵 MN×Wt M t N × W 时，利用 content-base addressing 和 dynamic memory allocation 两种寻址方式的组合，以确定哪些内存空间是可以写入的。DNC单元在从内存单元 MN×Wt M t N × W 读取向量时，利用 content-base addressing 和 temporal memory linkage 两种寻址方式的组合，以确定哪些内存空间是需要读出的。由此可知，共有3种寻址方式被利用进行读写，下面的部分将分别介绍这3种寻址机制，并解释如何写入和读取内存单元。

在介绍3中寻址机制之前，本节需要引入另一个变量空间 ΔN Δ N ，定义如下：

ΔN={α∈ℝN:αi∈[0,1],∑Ni=1αi⩽1} Δ N = { α ∈ R N : α i ∈ [ 0 , 1 ] , ∑ i = 1 N α i ⩽ 1 }

写操作

写操作，利用一个write weighting wwt∈ΔN w t w ∈ Δ N ，并通过控制信息中的the erase vector: et=σ(et^)∈[0,1]W e t = σ ( e t ^ ) ∈ [ 0 , 1 ] W 和 the write vector: vt∈ℝW v t ∈ R W 对内存矩阵进行操作，操作如下：

Mt=Mt−1⊙(E−wwtet)+wwtvt M t = M t − 1 ⊙ ( E − w t w e t ) + w t w v t

其中，write weighting wwt∈ΔN w t w ∈ Δ N 将在通过下文所述的寻址机制进行获取。

读操作

论文规定，利用R个read weighting {wr,1t,...,wr,Rt},wr,it∈ΔN { w t r , 1 , . . . , w t r , R } , w t r , i ∈ Δ N 从内存矩阵中读出R个read vector {r1t,...,rRt},rit∈RW { r t 1 , . . . , r t R } , r t i ∈ R W ，操作如下：

rit=MTtwr,it r t i = M t T w t r , i

其中，R个read weighting {wr,1t,...,wr,Rt},wr,it∈ΔN { w t r , 1 , . . . , w t r , R } , w t r , i ∈ Δ N 将在通过下文所述的寻址机制进行获取。

4.1 Content-based addressing

Content-based addressing 机制可以理解为一种attention机制。论文规定，对于内存矩阵 M∈ℝN×W M ∈ R N × W 中的第i个内存单元 M[i]∈ℝ1×W M [ i ] ∈ R 1 × W 在read 或 write 时所分配的比重 C(M,k,β)[i] C ( M , k , β ) [ i ] 定义如下：

C(M,k,β)[i]=exp{D(k,M[i,:])β}∑jexp{D(k,M[j,:])β} C ( M , k , β ) [ i ] = e x p { D ( k , M [ i , : ] ) β } ∑ j e x p { D ( k , M [ j , : ] ) β }

其中，函数 D(u,v) D ( u , v ) 是求两个向量之间的余弦值，以余弦值来衡量两个向量之间的相关程度，定义如下：

D(u,v)=u⋅v|u||v| D ( u , v ) = u ⋅ v | u | | v |

由以上定义可知， C(M,k,β)∈SN C ( M , k , β ) ∈ S N 确定了read head 和 write head 在内存矩阵 M∈ℝN×W M ∈ R N × W 上对各个内存单元 M[i]∈ℝ1×W M [ i ] ∈ R 1 × W 的读写比重。

4.2 Dynamic memory allocation

在某些情况下，我们需要对内存矩阵 MN×Wt M t N × W 中的某些内存单元进行释放并重新分配，所以论文加入Dynamic memory allocation 机制。

存储器用 ut∈[0,1]N u t ∈ [ 0 , 1 ] N 表示在t时刻内存单元的使用情况，并定义开始时刻 u0=0 u 0 = 0 。存储器在写入向量之前，需要确定哪些内存单元是可以被覆盖掉的，这就需要一个链表 free list 来表示覆写内存单元的顺序。存储器用 ψt∈[0,1]N ψ t ∈ [ 0 , 1 ] N 表示每个内存单元将被保留多少，定义如下：

ψt=∏Ri=1(1−fitwr,it−1) ψ t = ∏ i = 1 R ( 1 − f t i w t − 1 r , i )

则 ut u t 可以被定义如下：

ut=(ut−1+wwt−1⋅(1−ut−1))⋅ψt u t = ( u t − 1 + w t − 1 w ⋅ ( 1 − u t − 1 ) ) ⋅ ψ t

之后，对 ut u t 进行升序排列，将排序后的索引所形成的排列作为 free list ϕt∈ℤN ϕ t ∈ Z N 。

这样，在t时刻，在Dynamic memory allocation 机制中，各个内存单元的写入权重the allocation weighting at∈ΔN a t ∈ Δ N ，可以定义为：

at[ϕt[j]]=(1−ut[ϕt[j]])∏j−1i=1ut[ϕt[i]] a t [ ϕ t [ j ] ] = ( 1 − u t [ ϕ t [ j ] ] ) ∏ i = 1 j − 1 u t [ ϕ t [ i ] ]

Write weight

综上所述，论文将各个内存单元在t时刻的写入权重 wwt∈ΔN w t w ∈ Δ N 定义如下：

wwt=gwt[gatat+(1−gat)cwt] w t w = g t w [ g t a a t + ( 1 − g t a ) c t w ]

其中， cwt=C(Mt−1,kwt,βwt)∈SN c t w = C ( M t − 1 , k t w , β t w ) ∈ S N 是Content-based addressing 机制中的各个内存单元在t时刻的写入权重； at∈ΔN a t ∈ Δ N 是Dynamic memory allocation 机制中各个内存单元在t时刻的写入权重，这两种机制的组合形成整个存储器的在t时刻对各个内存单元的写入权重 wwt w t w 。

4.3 Temporal memory linkage

有时，用户希望网络能够将写入内存的内容按照一定的顺序读出来，于是论文设计了Temporal memory linkage机制。

这种机制拥有一个存储写入顺序的单元 Lt∈[0,1]N×N L t ∈ [ 0 , 1 ] N × N ，其中 Lt[i,j] L t [ i , j ] 表示在写入第j个内存单元之后写入第i个内存单元的权重(degree)， Lt[i,:]∈ΔN L t [ i , : ] ∈ Δ N ， Lt[:,j]∈ΔN L t [ : , j ] ∈ Δ N 。

在定义 Lt L t 之前，论文定义了一个优先权重(precedence weighting) pt∈ΔN p t ∈ Δ N ， pt[i] p t [ i ] 表示第i个内存单元是最后一次写入的权重(degree)，定义如下：

p0=0 p 0 = 0
pt=(1−∑iwwt[i])pt−1+wwt p t = ( 1 − ∑ i w t w [ i ] ) p t − 1 + w t w

然后， Lt L t 定义如下：

L0[i,j]=0;∀i,j L 0 [ i , j ] = 0 ; ∀ i , j
Lt=0;∀i L t = 0 ; ∀ i
Lt=(1−wwt[i]−wwt[j])Lt−1[i,j]+wwt[i]pt−1[j] L t = ( 1 − w t w [ i ] − w t w [ j ] ) L t − 1 [ i , j ] + w t w [ i ] p t − 1 [ j ]

The rows and columns
of Lt L t represent the weights of the temporal links going into and out from particular
memory slots, respectively.

给定 Lt L t ，the backward weighting bit∈ΔN b t i ∈ Δ N and forward weighting fit∈ΔN f t i ∈ Δ N for each read head i are defined as:

bit=LTtwr,it−1 b t i = L t T w t − 1 r , i
fit=Ltwr,it−1 f t i = L t w t − 1 r , i

其中， wr,it−1 w t − 1 r , i 表示第i个read head在t-1时刻的read weighting 。

Read weighting

综上所述， 论文定义第i个read head 在t时刻的 read weighting wr,it∈ΔN w t r , i ∈ Δ N 如下：

wr,it=πit[1]bit+πit[2]cr,it+πit[3]fit w t r , i = π t i [ 1 ] b t i + π t i [ 2 ] c t r , i + π t i [ 3 ] f t i

其中， πit∈S3 π t i ∈ S 3 是read mode控制信号， cr,it∈SN c t r , i ∈ S N 是Content-based addressing机制中得出的权重。content-based addressing 机制与Temporal memory linkage 机制的组合共同确定了第i个read head 在t时刻的read weighting wr,it w t r , i 。

time ------------------------------------------>

                +-------------------------------+
  mask:         |0000000001111111111111111111111|
                +-------------------------------+

                +-------------------------------+
  target:       |                              1| 'end-marker' channel.
                |         101100110110011011001 |
                |         010101001010100101010 |
                +-------------------------------+

                +-------------------------------+
  observation:  | 1011001                       |
                | 0101010                       |
                |1                              | 'start-marker' channel
                |        3                      | 'num-repeats' channel.
                +-------------------------------+