机器学习之神经网络学习及其模型
1、神经元模型
历史上，科学家一直希望模拟人的大脑，造出可以思考的机器。人为什么能够思考？科学家发现，原因在于人体的神经网络。
神经网络最基本的成分是神经元模型
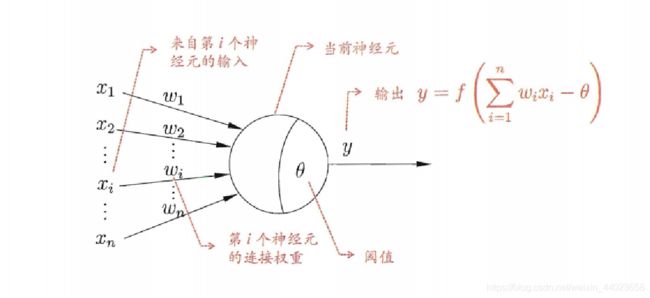其中，W表示的是向量，代表的是权重，函数f称为激活函数，
- 其中f()我们一般选择sigmoid函数（这里选择对数几率函数）
- 对数几率函数相较于阶跃函数优点：连续光滑，任意阶可导
2、感知机与多层网络
感知器的例子
城里正在举办一年一度的游戏动漫展览，小明拿不定主意，周末要不要去参观。
他决定考虑三个因素。
天气：周末是否晴天？
同伴：能否找到人一起去？
价格：门票是否可承受？
这就构成一个感知器。上面三个因素就是外部输入，最后的决定就是感知器的输出。如果三个因素都是 Yes（使用1表示），输出就是1（去参观）；如果都是 No（使用0表示），输出就是0（不去参观）。
单层感知机：有两层神经元组成，只有一层M-P神经元的网络模
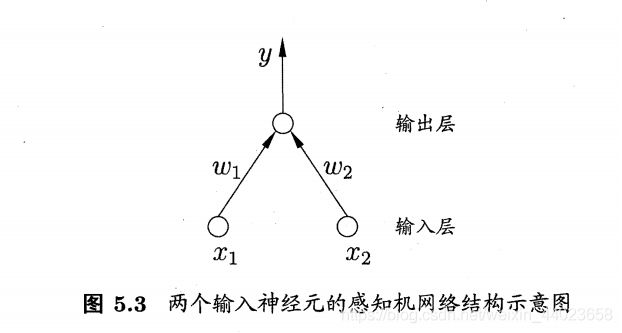单层感知机学习参数的调整
单层感知机只能解决线性可分的问题，对于非线性可分问题，需要考虑使用
多层功能神经元
多层前馈神经网络：
- 多层：有隐含层
- 前馈：不存在信号的逆向传播，不存在环和回路
- 不存在同层连接，不存在跨层连接
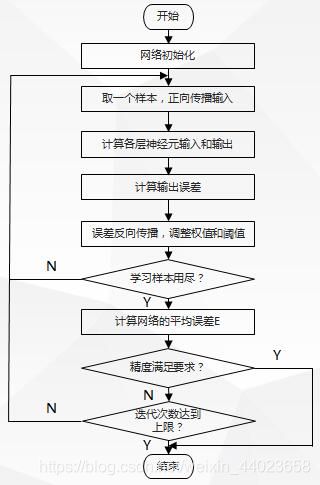
3、误差逆传播算法
BP算法（误差逆传播算法）
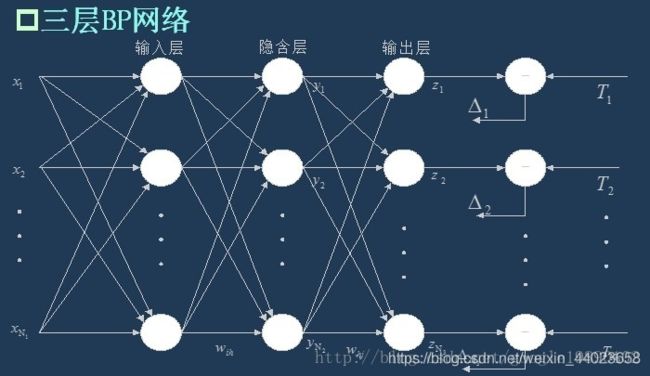
1.初始化
2.反复调整（信号向前传播->误差逆向传播->权值与阈值更新）
BP神经网络的过程主要分为两个阶段，第一阶段是信号的前向传播，从输入层经过隐含层，最后到达输出层；第二阶段是误差的反向传播，从输出层到隐含层，最后到输入层，依次调节隐含层到输出层的权重和偏置，输入层到隐含层的权重和偏置。
训练流程图
BP算法可能出现的问题
1.初始化问题：
初始化为不同的小随机数
不同：保证网络可以学习
小随机数：防止过大提前进入饱和状态
如果跌入局部最优，就要重新初始化
2.步长设置问题：
学习率（0到1之间）控制着算法的每一轮迭代中更新的步长
若太大，容易发生振荡，若太小，收敛速度缓慢。
3.结构学习问题：
- 输入层个数： 若给点属性为连续值，则等于训练数据的维度 若为离散值，等于维度+编码方式
- 输出层个数： 若为分类问题，与待分类类别数目大致成二为底的对数函数关系
- 隐层神经元个数： 试错法或者经验确定
一个包含足够多神经元的隐层，多层前馈神经网络就可以任意精度比较任意函数，所以，总可以找到一个合适的隐层神经元个数。
4.权值阈值更新问题：
-
标准BP算法：
每次更新只针对单个样例，参数更新非常频繁，不同样例的更新效果可能会有“抵消现象”，为了达到累计误差最小点，可能需要更多次的迭代。
-
累计BP算法：
直接针对累计误差最小化，读取整个数据集D之后才更新一次，更新频率低。但降到一定程度时，下降非常缓慢。
5.过拟合问题： -
过拟合：训练误差持续降低，但是测试误差却上升
解决策略
①早停
②正则化
4、全局最小和局部最小
由于初始化的时候随机初始化为不同的随机小数，则很有可能将网络跌入局部最优。不同的初始点，可能得到的最优解可能不同。
跳出局部最优的策略：
- 以多组不同参数值初始化多个神经网络，从不同 的点开始搜索最优点，可能会得到的结果不同， 从中选择有可能获得更接近全局最小的结果。
- 模拟退火技术
模拟退火在每一步都以一定概率接受比当前解更差 的结果，从而有助于跳出局部最优。 - 使用随机梯度下降，即使跌入局部极小点，因为 加入了随机因素，可能跳出局部最优。
5、常见的其他神经网络
1.RBF网络
单隐层前馈神经网络
使用径向基函数作为隐层神经元激活函数，输出层是对隐层神经元输出的线性组合
2.ART网络
竞争学习型，由比较层，识别层，识别阈值和重置模块组成
有较好的“可塑性，稳定性”
可进行增量学习，在线学习
3.SOM网络
竞争学习型的无监督神经网络，将高维输入数据映射到低维空间
4.级联相关网络
不仅学习连接权，阈值，还要学习网络结构。希望在训练过程中找到最符合数据特点的网网络结构。
5.Elman网络
允许网络中出现环状结构，从而可以让一些神经元的输出反馈回来作为输入信号。
6、神经网络的例子
所谓"车牌自动识别"，就是高速公路的探头拍下车牌照片，计算机识别出照片里的数字。
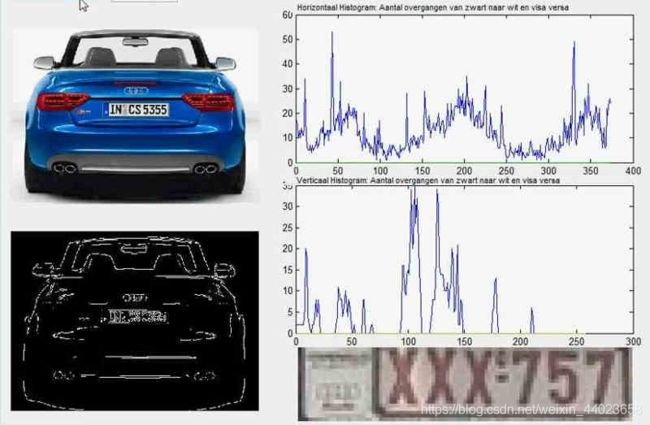这个例子里面，车牌照片就是输入，车牌号码就是输出，照片的清晰度可以设置权重（w）。然后，找到一种或多种图像比对算法，作为感知器。算法的得到结果是一个概率，比如75%的概率可以确定是数字1。这就需要设置一个阈值（b）（比如85%的可信度），低于这个门槛结果就无效。
一组已经识别好的车牌照片，作为训练集数据，输入模型。不断调整各种参数，直至找到正确率最高的参数组合。以后拿到新照片，就可以直接给出结果了。
7、输出的连续性
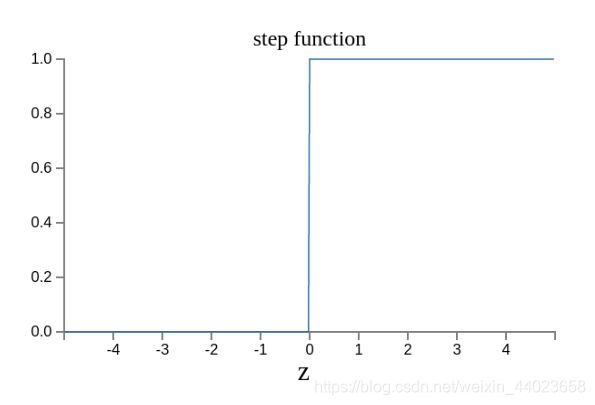
上面的模型有一个问题没有解决，按照假设，输出只有两种结果：0和1。但是，模型要求w或b的微小变化，会引发输出的变化。如果只输出0和1，未免也太不敏感了，无法保证训练的正确性，因此必须将"输出"改造成一个连续性函数。
这就需要进行一点简单的数学改造。
首先，将感知器的计算结果wx + b记为z。
z = wx + b
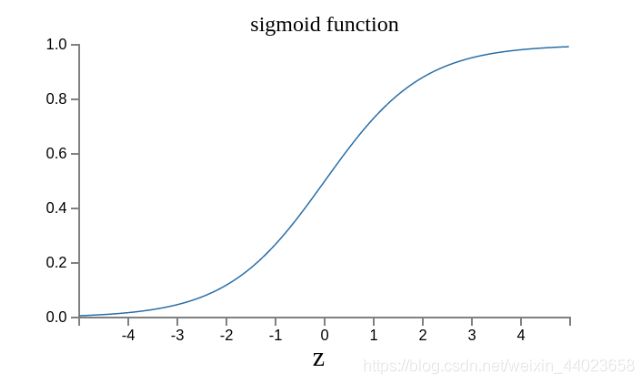
然后，计算下面的式子，将结果记为σ(z)。
σ(z) = 1 / (1 + e^(-z))
这是因为如果z趋向正无穷z → +∞（表示感知器强烈匹配），那么σ(z) → 1；如果z趋向负无穷z → -∞（表示感知器强烈不匹配），那么σ(z) → 0。也就是说，只要使用σ(z)当作输出结果，那么输出就会变成一个连续性函数。
原来的输出曲线是下面这样。
现在变成了这样。
推荐博客
神经网络，BP算法，计算图模型