浅谈模型鲁棒性
模型鲁棒性的理解
“鲁棒”的英文是robustness,其是一个特别大的研究领域。最权威的著作当属稳健统计的2本厚书 文献[1]和[2]。
1. 概念
. Huber从稳健统计的角度系统地给出了鲁棒性3个层面的概念:
一是模型具有较高的精度或有效性,这也是对于机器学习中所有学习模型的基本要求;
二是对于模型假设出现的较小偏差,只能对算法性能产生较小的影响;
主要是:噪声(noise)
三是对于模型假设出现的较大偏差,不可对算法性能产生“灾难性”的影响。
主要是:离群点(outlier)
2. 聚类算法的鲁棒性:
1) 定义
对于聚类算法而言,鲁棒性意味着聚类结果不应受到模型中存在的数据扰动、噪声及离群点的太大影响。
2) 综述文章
文献[4] [5]
3. 提升 对离群点数据鲁棒性 的方法
1)lp范数,0 2)采取鲁棒的数据模型 https://blog.csdn.net/zhouxinxin0202/article/details/79915873 分类的准确度长期以来都是评价图像分类模型性能的最核心甚至唯一标准。但最近研究表明,即使是充分训练好的深度神经网络模型也很容易被对抗攻击算法攻破。对抗攻击是指在图像上加入特定的且人眼无法察觉的微量噪声,使得目标模型对加噪之后得到的对抗样本做出错误分类。 [1] Huber P J. Robust Statistics[J]. 1981. Wiley, New York. [2] Hampel F R, Ronchetti E M, Rousseeuw P J, et al. Robust statistics: the approach based on influence functions[J]. 1986. Wiley, New York. [3] http://web.engr.oregonstate.edu/~tgd/talks/dietterich-aaai-presidents-address-final.pdf [4] Luis Angel García-Escudero, Alfonso Gordaliza, Carlos Matrán, et al. A review of robust clustering methods[J]. Advances in Data Analysis and Classification, 2010, 4(2-3):89-109. [5] Dave R N, Krishnapuram R. Robust clustering methods: a unified view[J]. IEEE Transactions on Fuzzy Systems, 2002, 5(2):270-293. [6] Nie F, Wang H, Cai X, et al. Robust Matrix Completion via Joint Schatten p-Norm and lp-Norm Minimization[C]// IEEE, International Conference on Data Mining. IEEE, 2013:566-574. [7] Meng D, Zhao Q, Xu Z. Improve robustness of sparse PCA by L1-norm maximization[J]. Pattern Recognition, 2012, 45(1): 487-497. [8] Forero P A, Kekatos V, Giannakis G B. Robust clustering using outlier-sparsity regularization[J]. IEEE Transactions on Signal Processing, 2012, 60(8): 4163-4177. [9] Mateos G, Giannakis G B. Robust PCA as bilinear decomposition with outlier-sparsity regularization[J]. IEEE Transactions on Signal Processing, 2012, 60(10): 5176-5190. [11] Hein, M., Andriushchenko, M.: Formal guarantees on the robustness of a classifier against adversarial manipulation. NIPS 2017. [12] Weng, T.W., Zhang, H., Chen, P.Y., Yi, J., Su, D., Gao, Y., Hsieh, C.J., Daniel, L.: Evaluating the robustness of neural networks: An extreme value theory approach. ICLR 2018. [13] Goodfellow, I., Shlens, J., Szegedy, C.: Explaining and harnessing adversarial examples. ICLR 2015. [14] Kurakin, A., Goodfellow, I.J., Bengio, S.: Adversarial machine learning at scale. ICLR 2017. [15] Carlini, N., Wagner, D.A.: Towards evaluating the robustness of neural networks. Oakland 2017. [16] Chen, P.Y., Sharma, Y., Zhang, H., Yi, J., Hsieh, C.J.: Ead: Elastic-net attacks to deep neural networks via adversarial examples. AAAI 2018文献[6]
文献[7] 给出了 一种鲁棒化PCA的方法,采用了L1范数。本人在博文[机器学习]Lasso,L1范数,及其鲁棒性中分析了L1范数相对于L2范数的鲁棒性,引用了文献[7]。
被广泛使用的数据模型: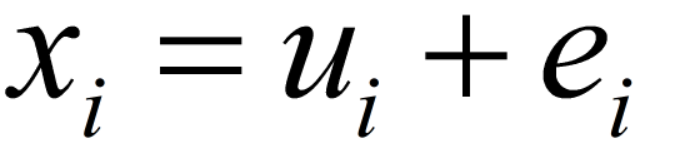
u--干净簇中心向量,e--噪声向量。
上述数据模型改造为: 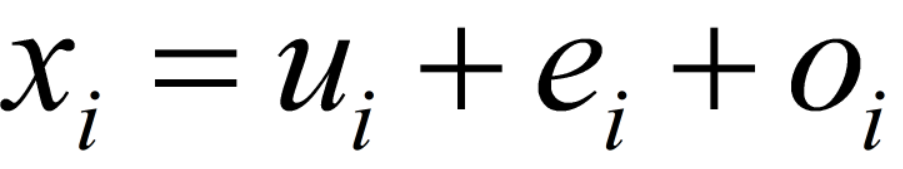
o--outlier。采用该数据模型,再在目标函数中引入关于o的惩罚项(如L1,L2范数),可提高算法鲁棒性。
参考文献:聚类 -- 文献[8], PCA -- 文献[9]
4. 未来发展:
TomDietterich教授表达了对人工智能鲁棒性的特别关注,参考文献[3] -- 一篇顶会的ppt。
5. 鱼(模型准确性)与熊掌(模型鲁棒性)难以兼得
为了揭示深度神经网络模型的鲁棒性和准确性之间的关系,来自 IBM 研究院,加州大学戴维斯分校,麻省理工学院以及京东 AI 研究院的研究人员,系统性地度量了 18 个被学术界和工业界广泛接受并使用的 ImageNet 深度神经网络模型,如 AlexNet、VGG Nets、Inception Nets、ResNets、DenseNets、MobileNets、NASNets 等的鲁棒性。
该研究发现了多个非常有趣的现象,包括:1) 准确度越高的模型的普遍鲁棒性越差,且分类错误率的对数和模型鲁棒性存在线性关系;2) 相比于模型的大小,模型的结构对于鲁棒性的影响更大;3) 黑盒迁移攻击是一直以来都比较困难的任务,但在 VGG 系列模型上生成的对抗样本可以比较容易地直接攻击其它的模型。该项工作对于理解深度神经网络准确性和鲁棒性之间关系提供了一个较完备的图景。此项研究的论文「Is Robustness the Cost of Accuracy? – A Comprehensive Study on the Robustness of 18 Deep Image Classification Models」已被欧洲计算机视觉大会(ECCV 2018)接收,并且预印版和代码都已公开。
为了评估深度神经网络的鲁棒性,一个直观的方法是使用对抗攻击。这种攻击生成视觉上和原图难以察觉区别的对抗样本使得深度神经网络做出错误分类。一般来讲,对于一个深度神经网络,如果在其上构建对抗样本越容易、所添加的噪声越小、则该网络越不鲁棒。除了对抗攻击之外,神经网络的鲁棒性也可以用一种独立于攻击的方式来衡量。例如 Szegedy 等人 [10] 和 Hein 等人 [11] 使用神经网络模型的全局和局部的 Lipschitz 常量对某些简单模型的鲁棒性进行了理论分析。Weng 等人 [12] 提出使用极值理论来估计为了生成有效的对抗样本所需要的最小噪声的尺度。
在这篇论文中,研究者们同时使用了上述两种方式评估了 18 个在 ImageNet 竞赛中脱颖而出的 DNN 模型,包括 AlexNet, VGG Nets, Inceptin Nets, ResNets, DenseNets, MobileNets 和 NASNets 等。这 18 个模型具有不同的大小,分类准确度和结构,因此具有充分的代表性,从而能更好地分析出影响模型鲁棒性的不同因素。在使用对抗攻击来评估鲁棒性的方式中,研究者们使用了目前最好最常用的几种攻击算法,包括 Fast Gradient Sign Method(FGSM)[13]、Iterative FGSM(I-FGSM)[14]、Carlini & Wagner(C&W)算法 [15],以及 Elastic-Net Attack under L1 norm(EAD-L1)算法 [16]。此外,在独立于攻击的鲁棒性评估方式中,研究者们选用了目前最为有效的 CLEVER Score[4] 来评估深度神经网络的鲁棒性。
这篇论文通过对 18 个 ImageNet 模型在 C&W 攻击和 I-FGSM 攻击下的鲁棒性的实验分析,发现当已有模型仅仅追求更高的分类准确度时,往往会牺牲在对抗攻击下的鲁棒性。
https://baijiahao.baidu.com/s?id=1608931340081979756&wfr=spider&for=pc
6. 参考文献:
[10] Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I., Fergus, R.: Intriguing properties of neural networks. ICLR 2014.