地图投影（一）高斯克吕格投影

程序定义一个投影的Transform的类，椭球ellipsoid为传入的参数，椭球相关的内容可见这篇博客

高斯投影正算是传入大地坐标与中央经线经度，计算得到该投影带独立坐标系下的坐标。若有要求可对y坐标东移，+500000，加以带号表示得到Y的通用坐标。

本程序高斯投影反算是在独立坐标系的前提下，输入点的xy坐标和中央经线经度，迭代计算得到大地经纬度。
计算时要分清是通用坐标还是独立坐标系下的坐标，不然会计算错误。
计算公式是由高斯投影正反算公式经过推导得到的适于电算的公式。

 class Transform
    {
     
        public double a;
        public double ec;
        public double ecc;
        public Transform(Ellipsoid ellipsoid)
        {
     
            a = ellipsoid.a;
            ec = ellipsoid.ec;
            ecc = ellipsoid.ecc;
        }
        //高斯投影正算
        public Pointxy BLToxy(PointBL bL,double L0)
        {
     
            double B = bL.B;
            double L = bL.L;
            //辅助计算公式
            double W = Math.Sqrt(1 - ec * Math.Sin(B) * Math.Sin(B));
            double n2 = ecc * Math.Cos(B) * Math.Cos(B);
            double t = Math.Tan(B);
            //曲率半径
            double N = a / W;
            double M = a * (1 - ec) / Math.Pow(W, 3);
            double M0 = a * (1 - ec);
            //子午线弧长计算公式
            double Ac = 1 + 3 / 4d * ec + 45 / 64d * Math.Pow(ec, 2) + 175 / 256d * Math.Pow(ec, 3) + 11025 / 16384d * Math.Pow(ec, 4) + 43659 / 65536d * Math.Pow(ec, 5);
            double Bc = 3 / 4d * ec + 15 / 16d * Math.Pow(ec, 2) + 525 / 512d * Math.Pow(ec, 3) + 2205 / 2048d * Math.Pow(ec, 4) + 72765 / 65536d * Math.Pow(ec, 5);
            double Cc = 15 / 64d * Math.Pow(ec, 2) + 105 / 256d * Math.Pow(ec, 3) + 2205 / 4096d * Math.Pow(ec, 4) + 10395 / 16384d * Math.Pow(ec, 5);
            double Dc = 35 / 512d * Math.Pow(ec, 3) + 315 / 2048d * Math.Pow(ec, 4) + 31185 / 131072d * Math.Pow(ec, 5);
            double Ec = 315 / 16384d * Math.Pow(ec, 4) + 3465 / 65536d * Math.Pow(ec, 5);
            double Fc = 693 / 131072d * Math.Pow(ec, 5);
            double Alpha = Ac * M0;
            double Beta = -1 / 2d * Bc * M0;
            double Gamma = 1 / 4d * Cc * M0;
            double Delte = -1 / 6d * Dc * M0;
            double Epsilon = 1 / 8d * Ec * M0;
            double Zeta = -1 / 10d * Fc * M0;
            //子午弧长
            double X = Alpha * B + Beta * Math.Sin(2 * B) + Gamma * Math.Sin(4 * B) + Delte * Math.Sin(6 * B) + Epsilon * Math.Sin(8 * B) + Zeta * Math.Sin(10 * B);
            //经差
            double l = L - L0 / 180 * Math.PI;
            //辅助量
            double a0 = X;
            double a1 = N * Math.Cos(B);
            double a2 = 1 / 2d * N * Math.Pow(Math.Cos(B), 2) * t;
            double a3 = 1 / 6d * N * Math.Pow(Math.Cos(B), 3) * (1 - Math.Pow(t, 2) + n2);
            double a4 = 1 / 24d * N * Math.Pow(Math.Cos(B), 4) * (5 - Math.Pow(t, 2) + 9 * n2 + 4 * Math.Pow(n2, 2));
            double a5 = 1 / 120d * N * Math.Pow(Math.Cos(B), 5) * (5 - 18 * Math.Pow(t, 2) + Math.Pow(t, 4) + 14 * n2 - 58 * n2 * Math.Pow(t, 2));
            double a6 = 1 / 720d * N * Math.Pow(Math.Cos(B), 6) * (61 - 58 * Math.Pow(t, 2) + Math.Pow(t, 4) + 270 * n2 - 330 * n2 * Math.Pow(t, 2)) * t;
            Pointxy xy = new Pointxy();
            xy.x = a0 + a2 * Math.Pow(l, 2) + a4 * Math.Pow(l, 4) + a6 * Math.Pow(l, 6);
            xy.y = a1 * l + a3 * Math.Pow(l, 3) + a5 * Math.Pow(l, 5);
            return xy;
        }
        /// 

        /// 高斯投影反算
        /// 
        /// <"高斯平面直角坐标系坐标">
        /// <"中央子午线经度">
        /// 
        public PointBL xyToBL(Pointxy xy,double L0)
        {
     
            double x = xy.x;
            double y = xy.y;
            double Ac = 1 + 3 / 4d * ec + 45 / 64d * Math.Pow(ec, 2) + 175 / 256d * Math.Pow(ec, 3) + 11025 / 16384d * Math.Pow(ec, 4) + 43659 / 65536d * Math.Pow(ec, 5);
            double Bc = 3 / 4d * ec + 15 / 16d * Math.Pow(ec, 2) + 525 / 512d * Math.Pow(ec, 3) + 2205 / 2048d * Math.Pow(ec, 4) + 72765 / 65536d * Math.Pow(ec, 5);
            double Cc = 15 / 64d * Math.Pow(ec, 2) + 105 / 256d * Math.Pow(ec, 3) + 2205 / 4096d * Math.Pow(ec, 4) + 10395 / 16384d * Math.Pow(ec, 5);
            double Dc = 35 / 512d * Math.Pow(ec, 3) + 315 / 2048d * Math.Pow(ec, 4) + 31185 / 131072d * Math.Pow(ec, 5);
            double Ec = 315 / 16384d * Math.Pow(ec, 4) + 3465 / 65536d * Math.Pow(ec, 5);
            double Fc = 693 / 131072d * Math.Pow(ec, 5);
            double M0 = a * (1 - ec);
            double Alpha = Ac * M0;
            double Beta = -1 / 2d * Bc * M0;
            double Gamma = 1 / 4d * Cc * M0;
            double Delte = -1 / 6d * Dc * M0;
            double Epsilon = 1 / 8d * Ec * M0;
            double Zeta = -1 / 10d * Fc * M0;
            double X = x;
            double B0 = X / Alpha;
            double Bf = 0;
            while (true)
            {
     
                double dert = Beta * Math.Sin(2 * B0) + Gamma * Math.Sin(4 * B0) + Delte * Math.Sin(6 * B0) + Epsilon * Math.Sin(8 * B0) + Zeta * Math.Sin(10 * B0);
                Bf = (X - dert) / Alpha;
                if (Math.Abs(Bf - B0) < 0.00000001)
                    break;
                else
                    B0 = Bf;
            }
            //辅助公式
            double Wf = Math.Sqrt(1 - ec * Math.Pow(Math.Sin(Bf), 2));
            double n2 = ecc * Math.Pow(Math.Cos(Bf), 2);
            double tf = Math.Tan(Bf);
            double Nf = a / Wf;
            double Mf = a * (1 - ec) / Math.Pow(Wf, 3);
            double b0 = Bf;
            double b1 = 1 / (Nf * Math.Cos(Bf));
            double b2 = -tf / (2 * Nf * Mf);
            double b3 = -(1 + 2 * tf * tf + n2) * b1 / (6 * Nf * Nf);
            double b4 = -(5 + 3 * tf * tf + n2 - 9 * n2 * tf * tf) * b2 / (12 * Nf * Nf);
            double b5 = -(5 + 28 * tf * tf + 24 * Math.Pow(tf, 4) + 6 * n2 + 8 * n2 * tf * tf) * b1 / (120 * Math.Pow(Nf, 4));
            double b6 = (61 + 90 * tf * tf + 45 * Math.Pow(tf, 4)) * b2 / (360 * Math.Pow(Nf, 4));
            PointBL BL = new PointBL();
            BL.B = b0 + b2 * Math.Pow(y, 2) + b4 * Math.Pow(y, 4) + b6 * Math.Pow(y, 6);
            BL.L = b1 * Math.Pow(y, 1) + b3 * Math.Pow(y, 3) + b5 * Math.Pow(y, 5) + L0 * Math.PI / 180;
            return BL;
        }
    }

测绘学科中的经纬度坐标一般为dd.mmssssss格式，如114.123345表示114°，12′，33.45″，用以下AngleRadian类进行弧度角度转换。

class AngleRadian
    {
     
        /// 

        /// dd.mmssssss格式的角度转换为弧度
        /// 
        /// 
        /// 
        public double ConvertDegreesToRadians(double degrees)
        {
     
            double d = Math.Truncate(degrees);
            double m = Math.Truncate((degrees - d) * 100);
            double s = ((degrees - d) * 100 - m) * 100;
            double radians = (d + m / 60 + s / 3600) / 180 * Math.PI;
            return radians;
        }
        /// 

        /// 弧度转换为dd.mmssssss格式的角度
        /// 
        /// 
        /// 
        public double ConvertRadiansToDegrees(double radians)
        {
     
            double dd = radians / Math.PI * 180;
            double d = Math.Truncate(dd);
            double m = Math.Truncate((dd - d) * 60);
            double s = Math.Round(((dd - d) * 60 - m) * 60, 4);//返回四位小数
            double degrees = d + m / 100 + s / 10000;
            return degrees;
            
        }
        /// 

        /// dd.mmssssss格式的角度转换为°′″形式的字符串
        /// 
        /// 
        /// 
        public string ConvertDegreesToString(double degrees)
        {
     
            string symbol = "";
            if (degrees < 0)
            {
     
                degrees = Math.Abs(degrees);
                symbol = "-";
            }
            double d = Math.Truncate(degrees);
            double m = Math.Truncate((degrees - d) * 100);
            double s = ((degrees - d) * 100 - m) * 100;
            string dms = symbol + d.ToString() + "°" + m.ToString() + "′" + s.ToString() + "″";
            return dms;
        }
        /// 

        /// 弧度转换为°′″形式的字符串
        /// 
        /// 
        /// 
        public string ConvertRadiansToString(double radians)
        {
     
            string symbol = "";
            if (radians < 0)
            {
     
                radians = Math.Abs(radians);
                symbol = "-";
            }
            double dd = radians / Math.PI * 180;
            double d = Math.Truncate(dd);
            double m = Math.Truncate((dd - d) * 60);
            double s = Math.Round(((dd - d) * 60 - m) * 60, 4);//返回四位小数
            string dms = symbol + d.ToString() + "°" + m.ToString() + "′" + s.ToString() + "″";
            return dms;
        }
    }

浅谈高斯投影

1、分带

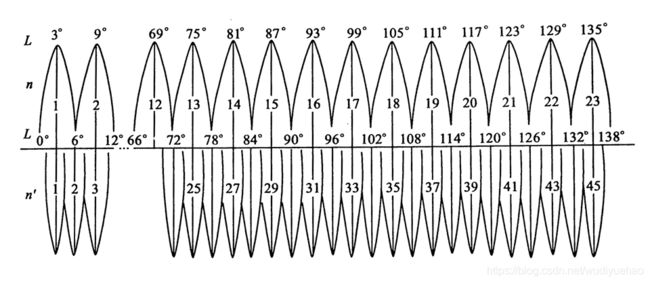
我国采用6、3度带。中央子午线与带号的关系
6度带
自格林威治零度经线起，每6度分为一个投影带，自西向东分带，全球共分为60个投影带，带号依次编为第 1、2…60带。我国6°带中央子午线的经度，由73°起每隔6°而至135°，共计11带，带号用n表示，中央子午线的经度用Ｌ０表示。
L=6n-3（n为带号，L为中央经线经度）
3度带
是在6度带的基础上分成的，它的中央子午线与六度带的中央子午线和分带子午线重合，即自 1.5度子午线起每隔经差3度自西向东分带，带号依次编为三度带第 1、2…120带。中央子午线经度依次为3°, 6°, 9°, … , 360°。
L=3n（n为带号，L为中央经线经度）

2、在我国x坐标都是正的，y坐标的最大值(在赤道上)约为330km。为了避免出现负的y坐标，则无论3°或6°带，每带的纵坐标轴要西移500 km，即在每带的横（y）坐标上加500 km。

为了指明该点属于何带，还规定在横坐标y值之前，要写上带号。
因此坐标值表现形式有三种：自然值、+500KM值、通用值。

所以拿到一个坐标应当进行判断它到底是哪一种类型的坐标值，本程序的转换是基于自然值的转换