老司机开车,教女朋友什么是「马拉车算法」
小白可点击图片进行预习
一、回文
正着、反着读都是一样的称为回文, e g \mathrm{eg} eg.121,abccba
回文有啥用呢?
写诗???考试出题。。。[复杂]
《 菩 萨 蛮 菩萨蛮 菩萨蛮》
苏轼
柳庭风静人眠昼,昼眠人静风庭柳。香汗薄衫凉,凉衫薄汗香。
手红冰碗藕,藕碗冰红手。郎笑藕丝长,长丝藕笑郎。
二、算法
解决这类回文串问题一般有四种算法
| 算法种类 | 时间复杂度 | 空间复杂度 | 描述 |
|---|---|---|---|
| B F BF BF | O ( n 3 ) O(n^3) O(n3) | O ( n 3 ) O(n^3) O(n3) | 遍历所有子字符串,子串数为 n 2 n^2 n2,长度平均为 n / 2 n/2 n/2 |
| d p dp dp | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | 两层循环,外层循环从后往前,内层循环从当前访问的字符到结尾 |
| 中心扩散法 | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 分奇偶两种情况,以 i i i为中心不断向两边扩展判断,无需额外空间 |
| M a n a c h e r Manacher Manacher | O ( n ) O(n) O(n) | O ( n ) O(n) O(n) | 无需向中心检测法分奇偶两种情况讨论,直接从左到右遍历一遍 |
-
Brute – force
根据回文串的定义,枚举所有长度 ≥ 2 ≥2 ≥2的子串,依次判断是否是回文串
#include这个 B F BF BF也没什么用,就是希望读者们在刷题时,要先想想暴力怎么打,然后在一步步优化,最后才是正解,而不是看完题就直接看题解。
-
DP(区间DP)
回文的 d p dp dp有点小难,不太会的建议不要深究(其实我自己的 d p dp dp也不是很好) ,只要知道时间复杂度和空间复杂度有就够了。(感兴趣的读者可以康康)
根据回文的定义可知:一个回文去掉等长的前后缀后,剩下的还是回文
- 如果一个字符串头尾两个字符都不相等,那么这个字符串肯定不是回文串
- 如果一个字符串两头的字符相等,再继续往下判断
- 如果里面的子串是回文串,那么整体就是回文串
- 如果里面的子串不是,那么整体也不是
在头尾字符相等的情况下,里面的子字符串的回文性质决定了整个子串的回文性质,我们可以简单粗暴地将这定义为状态
f i r s t first first 状 态 状态 状态
d p [ i ] [ j ] dp[i][j] dp[i][j]表示子串 s [ i ] → s [ j ] s[i] \to s[j] s[i]→s[j]是否为回文串
s e c o n d second second 状 态 转 移 方 程 状态转移方程 状态转移方程
if(s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1];
- 由于构成子串,因此
i ≤ j,所以我们只需填这张纸对角线以上的部分。 - 看到
dp[i + 1][j - 1]就得考虑到边界问题
边界条件:[i + 1, j - 1]不构成区间,即长度小于 2 2 2,即(j - 1) - (i + 1) < 2,整理得:j - i < 3,显然,j - i < 3 < = > <=> <=> j - i + 1 < 4,即子串s[i] -> s[j]长度等于 2 2 2或 3 3 3时,只需判断头尾两字符是否相等即可下结论。
if(s[i] == s[j] && j - i < 2) dp[i][j] = 1;
else dp[i][j] = dp[i + 1][j - 1];
t h i r d third third 初 始 化 初始化 初始化
单个字符一定是回文串,因此把对角线初始化为 1 1 1
for(register int i = 1; i <= n; ++i) dp[i][i] = 1;
其实初始化可以省去,应为只有一个字符一定是回文,dp[i][j]根本不会被其他状态值更新的
f o r t h forth forth 输 出 输出 输出
只要得到dp[i][j] = 1,记录回文串的「起始位置」和「回文长度」即可。
f i f t h fifth fifth 优 化 空 间 优化空间 优化空间
在填表的过程中,只考虑了左下方的数值。
#include-
中心扩散法
b f bf bf是采用双指针来验证是否是回文串。
那 我 们 可 以 怎 么 实 现 优 化 呢 ? 那我们可以怎么实现优化呢? 那我们可以怎么实现优化呢?
- 比较容易想到枚举可能是回文串的“中心位置”,从“中心位置”向两边扩散出去,得到一个回文串。
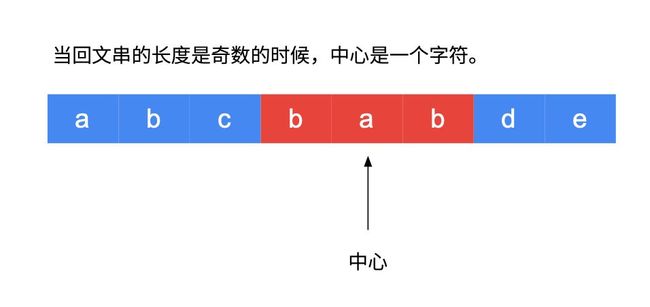
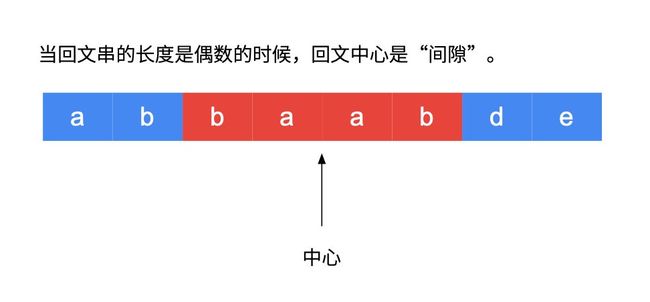
但这里需要注意一个细节:我们需要分成奇偶两种情况
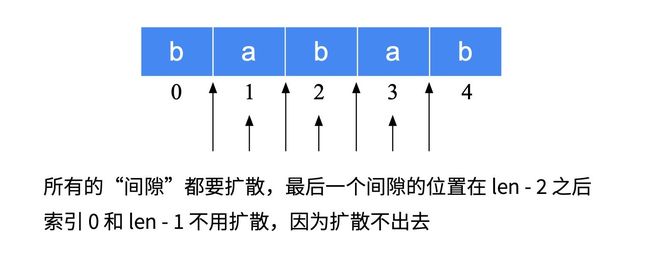
那 如 何 找 下 一 个 字 符 串 可 能 的 回 文 子 串 的 “ 中 心 ” 呢 ? 那如何找下一个字符串 可能的回文子串的“中心”呢? 那如何找下一个字符串可能的回文子串的“中心”呢?
1.如果传入重合的索引编码,得到的回文串长为奇数
2.如果传入相邻的索引编码,得到的回文串长为偶数
#include-
Manather
-
( 1 ) 解 决 奇 偶 性 (1)解决奇偶性 (1)解决奇偶性
M a n a c h e r Manacher Manacher算法先对字符串做了一个预处理,在所有空隙中插入同样的某种任意的字符(不包括原串内的字符),这样就使得所有的串都是奇数的长度。(一般插'#'字符)
aba ——> #a#b#a#
abba ——> #a#b#b#a#
- 解 决 重 复 访 问 解决重复访问 解决重复访问
概念引入:回文串最左或最右与其对称轴的距离称为回文半径
用len[i]表示第 i i i字符为对称轴的回文串的长度,(我们一般对字符串从左到右处理),所以len[i]为枚举第 i i i个字符为对称轴的回文串的长度
模 板 题 模板题 模板题
#include三、有趣的回文
-
单词
tattarrattat是牛津词典中最长的回文单词,出现于爱尔兰作家詹姆斯 · 乔伊斯的小说《尤利西斯》,是敲门的意思 -
吉尼斯纪录的最长回文单词是
detartrated,是化学术语