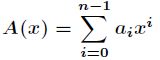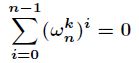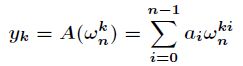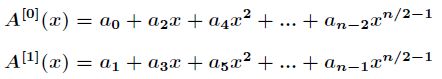莫比乌斯反演
莫比乌斯反演在数论中占有重要的地位，许多情况下能大大简化运算。那么我们先来认识莫比乌斯反演公式。
定理：
和
是定义在非负整数集合上的两个函数，并且满足条件
，那么我们得到结论
在上面的公式中有一个
函数，它的定义如下：
（1）若
，那么
（2）若
，
均为互异素数，那么
（3）其它情况下
对于函数，它有如下的常见性质：
（1）对任意正整数
有
（2）对任意正整数有
线性筛选求莫比乌斯反演函数代码。
void Init()
{
memset(vis,0,sizeof(vis));
mu[1] = 1;
cnt = 0;
for(int i=2; i有了上面的知识，现在我们来证明莫比乌斯反演定理。
证明
证明完毕！
嗯，有了莫比乌斯反演，很多问题都可以简化了，接下来我们来看看莫比乌斯反演在数论中如何简化运算的。
题目：http://bz.cdqzoi.com/JudgeOnline/problem.php?id=2818
题意：给一个正整数，其中
，求使得
为质数的
的个数，
。
分析：对于本题，因为是使得为质数，所以必然要枚举小于等于的质数，那么对于每一个质数
，只
需要求在区间
中，满足有序对互质的对数。
也就是说，现在问题转化为：在区间
中，存在多少个有序对使得互质，这个问题就简单啦，因为
是有序对，不妨设
，那么我们如果枚举每一个
，小于有多少个
与互素，这正是欧拉函数。所以
我们可以递推法求欧拉函数，将得到的答案乘以2即可，但是这里乘以2后还有漏计算了的，那么有哪些呢？
是
且为素数的情况，再加上就行了。
代码：
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 10000010;
bitset prime;
LL phi[N];
LL f[N];
int p[N];
int k;
void isprime()
{
k = 0;
prime.set();
for(int i=2; i>= 1;
for(int i=3; i 上题不算太难，普通的欧拉函数就可以搞定，接下来我们来看看它的升级版。
题意：给定两个数
和
，其中
，
，求
为质数的
有多少对？其中和的范
围是
。
分析：本题与上题不同的是和不一定相同。在这里我们用莫比乌斯反演来解决，文章开头也说了它能大大简化
运算。我们知道莫比乌斯反演的一般描述为：
其实它还有另一种描述，本题也是用到这种。那就是：
好了，到了这里，我们开始进入正题。。。
对于本题，我们设
为满足
且和的的对数
为满足
且和的的对数
那么，很显然
，反演后得到
因为题目要求是为质数，那么我们枚举每一个质数
，然后得到
如果直接这样做肯定TLE，那么我们必须优化。
我们设
，那么继续得到
。
到了这里，可以看出如果我们可以先预处理出所有的
对应的
的值，那么本题就解决了。
我们设
，注意这里为素数，
。
那么，我们枚举每一个
，得到
，现在分情况讨论：
（1）如果整除
，那么得到
（2）如果不整除，那么得到
代码：
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 10000005;
bool vis[N];
int p[N];
int cnt;
int g[N],u[N],sum[N];
void Init()
{
memset(vis,0,sizeof(vis));
u[1] = 1;
cnt = 0;
for(int i=2;i>n>>m;
if(n > m) swap(n,m);
LL ans = 0;
for(int i=1,last;i<=n;i=last+1)
{
last = min(n/(n/i),m/(m/i));
ans += (n/i)*(m/i)*(sum[last]-sum[i-1]);
}
cout< 多项式乘法运算初级版——快速傅里叶变换
快速傅里叶变换在信息学竞赛中主要用于求卷积，或者说多项式乘法。我们知道，多项式乘法的普通算法时间复杂度
是
，通过快速傅里叶变换可以使时间降为
，那么接下来会详细介绍快速傅里叶变换的原理。
首先来介绍多项式的两种表示方法，即系数表示法和点值表示法。从某种意义上说，这两种方法是等价的。先设
（1）系数表示法
对于一个次数界为
的多项式
来说，其系数表示法就是一个由系数组成的向量
，很
明显，这样的多项式乘法运算的时间复杂度为。
（2）点值表示法
对于一个次数界为的多项式来说，其点值是个点值对所形成的集合
其中
各不相同，并且当
时，有
。可以看出一个多项式可以有多种不同的点值
表示法，而通过这个不同的点值对可以表示一个唯一的多项式。而通过点值表示法来计算多项式的乘法，时间
复杂度为
。
从原则上来说，计算多项式的点值是简单易行的，因为我们只需要先选取个相异的点，然后通过秦九韶算法可
以在时间内求出所有的
，实际上如果我们的选得巧妙的话，就可以加速这一过程，使其运行时间变
为。
根据多项式的系数表示法求其点值表示法的过程称为求值，而根据点值表示法求其系数表示法的过程称为插值。
对于求卷积或者说多项式乘法运算问题，先是通过傅里叶变换对系数表示法的多项式进行求值运算，这一步的时
间复杂度为
，然后在时间内进行点值相乘，再进行插值运算。
那么，接下来就是我们今天的重点了，如何高效地对一个多项式进行求值运算，即将多项式的表示法变为点值表示法。
如果选取单位复根作为求值点，则可以通过对系数向量进行离散傅里叶变换（DFT），得到相应的点值表示。同样地
也可以通过对点值对进行逆DFT运算，获得相应的系数向量。DFT和逆DFT的时间复杂度均为。
一. 求DFT
选取
次单位复根作为
来求点值是比较巧妙的做法。
次单位复根是满足
的复数
，次单位复根恰好有个，它们是
，
，为
了解释这一式子，利用复数幂的定义
，值
称为主次单位根，所有其
它次单位复根都是
的次幂。
个次单位复根
在乘法运算下形成一个群，该群的结构与加法群
模相同。
接下来认识几个关于次单位复根的重要性质。
（1）相消引理
对于任何整数
，有
（2）折半引理
如果
且为偶数，则
（3）求和引理
对任意整数
和不能被
整除的非零整数
，有
回顾一下，我们希望计算次数界为
的多项式
在
处的值，假定是2的幂，因为给定的次数界总可以增大，如果需要，总可以添加值为零
的新的高阶系数。假定已知
的系数形式为
，对
，定义结果
如下
向量
是系数向量
的离散傅里叶变换，写作
。
通过使用一种称为快速傅里叶变换（FFT）的方法，就可以在
时间内计算出
，而直接
计算的方法所需时间为
，FFT主要是利用单位复根的特殊性质。FFT方法运用了分治策略，它用
中偶数下标的系数与奇数下标的系数，分别定义了两个新的次数界为
的多项式
和
则进一步有
这样
在
处的值得问题就转换为求次数界为
的多项式和在点
处的值。由于在奇偶分类时导致顺序发生变化，所以需要先通过Rader算法进行
倒位序，在FFT中最重要的一个操作是蝴蝶操作，通过蝴蝶操作可以将前半部分和后半部分的值求出。
题目：http://acm.hdu.edu.cn/showproblem.php?pid=1402
题意：大数乘法，需要用FFT实现。
代码：
#include
#include
#include
#include
using namespace std;
const int N = 500005;
const double PI = acos(-1.0);
struct Virt
{
double r, i;
Virt(double r = 0.0,double i = 0.0)
{
this->r = r;
this->i = i;
}
Virt operator + (const Virt &x)
{
return Virt(r + x.r, i + x.i);
}
Virt operator - (const Virt &x)
{
return Virt(r - x.r, i - x.i);
}
Virt operator * (const Virt &x)
{
return Virt(r * x.r - i * x.i, i * x.r + r * x.i);
}
};
//雷德算法--倒位序
void Rader(Virt F[], int len)
{
int j = len >> 1;
for(int i=1; i> 1;
while(j >= k)
{
j -= k;
k >>= 1;
}
if(j < k) j += k;
}
}
//FFT实现
void FFT(Virt F[], int len, int on)
{
Rader(F, len);
for(int h=2; h<=len; h<<=1) //分治后计算长度为h的DFT
{
Virt wn(cos(-on*2*PI/h), sin(-on*2*PI/h)); //单位复根e^(2*PI/m)用欧拉公式展开
for(int j=0; j=0; i--)
{
if(result[i])
{
high = i;
break;
}
}
for(int i=high; i>=0; i--)
printf("%d",result[i]);
puts("");
}
int main()
{
while(~scanf("%s%s",str1,str2))
{
Init(str1,str2);
Work();
Export();
}
return 0;
} 题目：http://acm.hdu.edu.cn/showproblem.php?pid=4609
题意：给定n条长度已知的边，求能组成多少个三角形。
分析：用一个num数组来记录次数，比如num[i]表示长度为i的边有num[i]条。然后对num[]求卷积，除去本身重
复的和对称的，然后再整理一下就好了。
代码：
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 400005;
const double PI = acos(-1.0);
struct Virt
{
double r,i;
Virt(double r = 0.0,double i = 0.0)
{
this->r = r;
this->i = i;
}
Virt operator + (const Virt &x)
{
return Virt(r+x.r,i+x.i);
}
Virt operator - (const Virt &x)
{
return Virt(r-x.r,i-x.i);
}
Virt operator * (const Virt &x)
{
return Virt(r*x.r-i*x.i,i*x.r+r*x.i);
}
};
//雷德算法--倒位序
void Rader(Virt F[],int len)
{
int j = len >> 1;
for(int i=1; i> 1;
while(j >= k)
{
j -= k;
k >>= 1;
}
if(j < k) j += k;
}
}
//FFT实现
void FFT(Virt F[],int len,int on)
{
Rader(F,len);
for(int h=2; h<=len; h<<=1) //分治后计算长度为h的DFT
{
Virt wn(cos(-on*2*PI/h),sin(-on*2*PI/h)); //单位复根e^(2*PI/m)用欧拉公式展开
for(int j=0; j>= 1;
sum[0] = 0;
for(int i=1; i<=len; i++)
sum[i] = sum[i-1] + num[i];
LL cnt = 0;
for(int i=0; i 多项式乘法运算终极版——NTT（快速数论变换）
在上一篇文章中 http://blog.csdn.net/acdreamers/article/details/39005227 介绍了用快速傅里叶变
换来求多项式的乘法。可以发现它是利用了单位复根的特殊性质，大大减少了运算，但是这种做法是对复数系数的矩阵
加以处理，每个复数系数的实部和虚部是一个正弦及余弦函数，因此大部分系数都是浮点数，我们必须做复数及浮点数
的计算，计算量会比较大，而且浮点数的计算可能会导致误差增大。
今天，我将来介绍另一种计算多项式乘法的算法，叫做快速数论变换（NTT），在离散正交变换的理论中，已经证明在
复数域内，具有循环卷积特性的唯一变换是DFT，所以在复数域中不存在具有循环卷积性质的更简单的离散正交变换。
因此提出了以数论为基础的具有循环卷积性质的快速数论变换。
回忆复数向量，其离散傅里叶变换公式如下
离散傅里叶逆变换公式为
今天的快速数论变换（NTT）是在
上进行的，在快速傅里叶变换（FFT）中，通过
次单位复根来运算的，即满
足
的
，而对于快速数论变换来说，则是可以将
看成是
的等价，这里
是模素数
的原根（由于是素数，那么原根一定存在）。即
所以综上，我们得到数论变换的公式如下
而数论变换的逆变换公式为
这样就把复数对应到一个整数，之后一切都是在
系统内考虑。
上述数论变换（NTT）公式中，要求
是素数且
必须是
的因子。由于
经常是2的方幂，所以可以构造形
如
的素数。通常来说可以选择
为费马素数，这样的变换叫做费马数数论变换。
这里我们选择
，
，这样得到模的原根值为
。
题目：http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1028
分析：题目意思就是大数相乘，此处用快速数论变换（NTT）实现。
代码：
#include
#include
#include
using namespace std;
typedef long long LL;
const int N = 1 << 18;
const int P = (479 << 21) + 1;
const int G = 3;
const int NUM = 20;
LL wn[NUM];
LL a[N], b[N];
char A[N], B[N];
LL quick_mod(LL a, LL b, LL m)
{
LL ans = 1;
a %= m;
while(b)
{
if(b & 1)
{
ans = ans * a % m;
b--;
}
b >>= 1;
a = a * a % m;
}
return ans;
}
void GetWn()
{
for(int i=0; i> 1;
for(int i=1; i> 1;
while(j >= k)
{
j -= k;
k >>= 1;
}
if(j < k) j += k;
}
}
void NTT(LL a[], int len, int on)
{
Rader(a, len);
int id = 0;
for(int h = 2; h <= len; h <<= 1)
{
id++;
for(int j = 0; j < len; j += h)
{
LL w = 1;
for(int k = j; k < j + h / 2; k++)
{
LL u = a[k] % P;
LL t = w * (a[k + h / 2] % P) % P;
a[k] = (u + t) % P;
a[k + h / 2] = ((u - t) % P + P) % P;
w = w * wn[id] % P;
}
}
}
if(on == -1)
{
for(int i = 1; i < len / 2; i++)
swap(a[i], a[len - i]);
LL Inv = quick_mod(len, P - 2, P);
for(int i = 0; i < len; i++)
a[i] = a[i] % P * Inv % P;
}
}
void Conv(LL a[], LL b[], int n)
{
NTT(a, n, 1);
NTT(b, n, 1);
for(int i = 0; i < n; i++)
a[i] = a[i] * b[i] % P;
NTT(a, n, -1);
}
void Transfer(LL a[], int n)
{
int t = 0;
for(int i = 0; i < n; i++)
{
a[i] += t;
if(a[i] > 9)
{
t = a[i] / 10;
a[i] %= 10;
}
else t = 0;
}
}
void Print(LL a[], int n)
{
bool flag = 1;
for(int i = n - 1; i >= 0; i--)
{
if(a[i] != 0 && flag)
{
printf("%d", a[i]);
flag = 0;
}
else if(!flag)
printf("%d", a[i]);
}
puts("");
}
int main()
{
GetWn();
while(scanf("%s%s", A, B)!=EOF)
{
int len;
Prepare(A, B, a, b, len);
Conv(a, b, len);
Transfer(a, len);
Print(a, len);
}
return 0;
}