SBT总结
SBT
什么是SBT
SBT即Size Balanced Tree,是一种高效的二叉查找树,复杂度非常稳定。
SBT保证的一个节点的子树大小与兄弟节点子树大小相同,这个特殊性质需要维护,也可以完成很多操作。
SBT的数组
struct SBT
{
int key,left,right,size;
}tree[100100];
其中key是节点的键值,left和right是节点左右子树,size是节点的大小。
子树大小的维护
树要满足一下条件:
tree[i].left.size>=max(tree[i].right.right.size,tree[i].right.left.size)
tree[i].right.size>=max(tree[i].left.left.size,tree[i].left.right.size)
我们思考我们要怎么维护子树大小。我们有一个常用的方法,就是旋转。
左旋和右旋
其实和treap,splay是相似的。比如:
void lrot(int &x)
{
int y=tree[x].right;
tree[x].right=tree[y].left;
tree[y].left=x;
tree[y].size=tree[x].size;//转上去的节点数量为先前此处节点的size
tree[x].size=tree[tree[x].left].size+tree[tree[x].right].size+1;
x=y;
}
void rrot(int &x)
{
int y=tree[x].left;
tree[x].left=tree[y].right;
tree[y].right=x;
tree[y].size=tree[x].size;
tree[x].size=tree[tree[x].left].size+tree[tree[x].right].size+1;
x=y;
}
与很多二叉查找树不同的是,不用记录父亲节点,所以旋转中不需要改变多少变量。
旋转是维护平衡的基础。
maintain函数
当我们插入一个点,树就可能不再平衡,我们使用的函数就是maintain函数。
maintain(x)指修复以x为根的树的平衡性。调用maintain(x)的前提条件是,x的左右子树都已平衡。
插入时我们要考虑四种情况。
分别是:
-
x.left.left.size>x.right.size
-
x.left.right.size>x.right.size
-
x.right.right.size>x.left.size
-
x.right.left.size>x.left.size
我们直接看一下代码。
void maintain(int &x,bool flag)
{
if(flag==false)//左边
{
if(tree[tree[tree[x].left].left].size>tree[tree[x].right].size)//左孩子的左子树大于右孩子
rrot(x);
else if(tree[tree[tree[x].left].right].size>tree[tree[x].right].size)//右孩子的右子树大于右孩子
{
lrot(tree[x].left);
rrot(x);
}
else return ;
}
else //右边
{
if(tree[tree[tree[x].right].right].size>tree[tree[x].left].size)//右孩子的右子树大于左孩子
lrot(x);
else if(tree[tree[tree[x].right].left].size>tree[tree[x].left].size)//右孩子的左子树大于左孩子
{
rrot(tree[x].right);
lrot(x);
}
else return ;
}
maintain(tree[x].left,false);
maintain(tree[x].right,true);
maintain(x,true);
maintain(x,false);
}
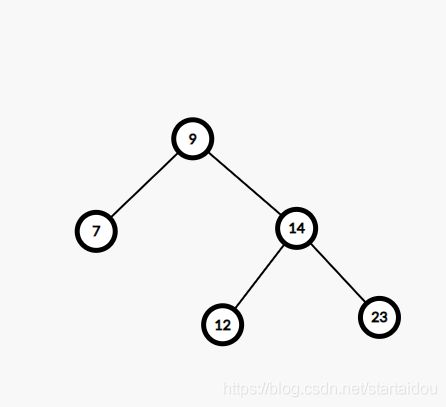
比如这样一张图

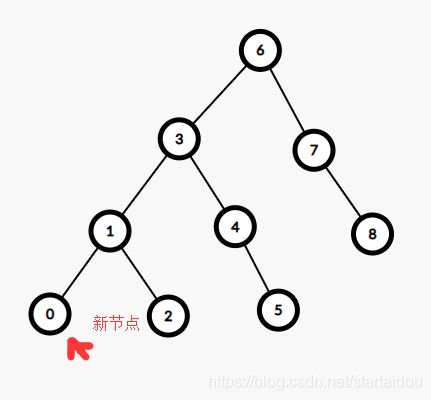
然后插入一个键值为0的点。insert(t,left,data),即insert(1,left,data)就是插在1的左边。
我们怎么处理这些情况呢?
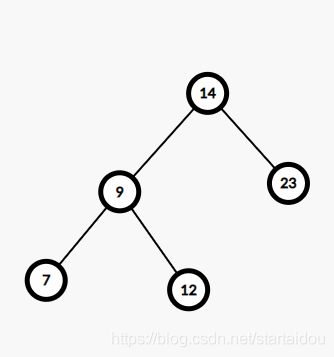
我们先让x右旋,即6右旋。
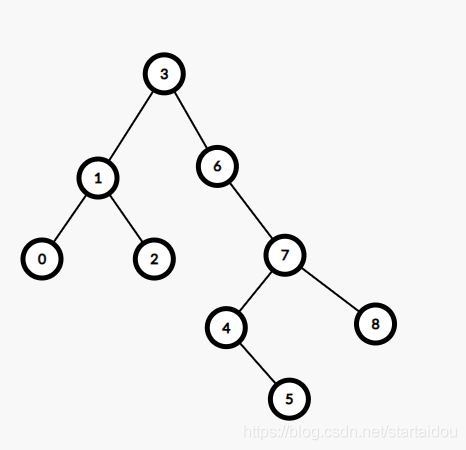
这个时候它已经满足条件了。
有时候我们不能一次旋转就可以达到平衡,所以要多次旋转。
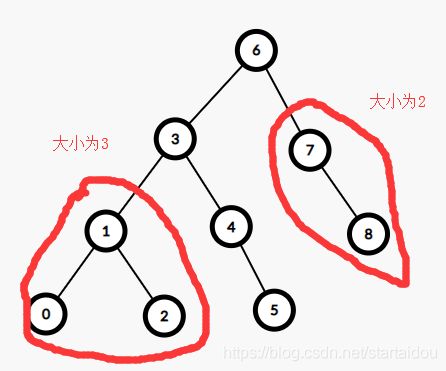
比如这种两次旋转。
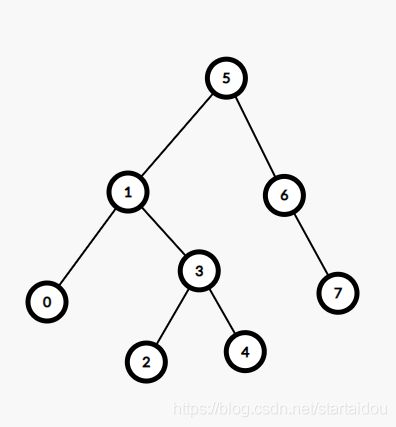
把3旋转到1。
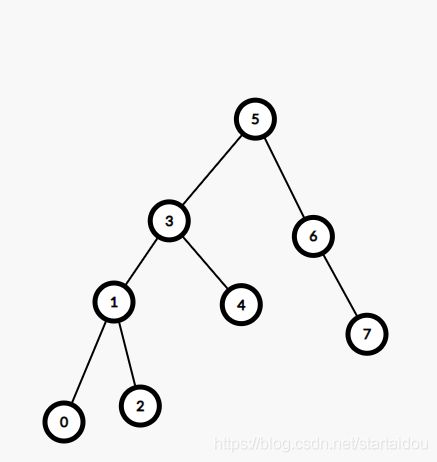
这样就和之前一次旋转一样了。
把3旋转到5。
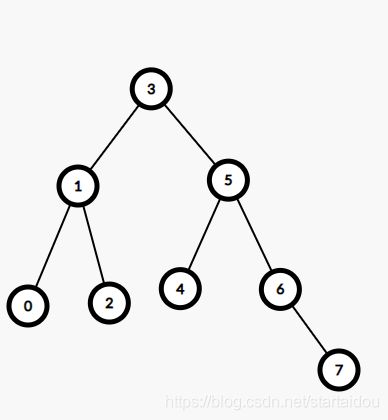
可能我们需要更多次旋转,但可以证明,最多旋转logn次。
现在我们就可以用SBT解决问题了。
其他操作
插入操作
void insert(int &x,int key)
{
if(x==0)
{
x=++top;
tree[x].left=tree[x].right=0;
tree[x].size=1;
tree[x].key=key;
}
else
{
++tree[x].size;
if(key<tree[x].key) insert(tree[x].left,key);
else insert(tree[x].right,key);//相同元素插入到右子树中
maintain(x,key>=tree[x].key);//每次插入把平衡操作压入栈中
}
}
前驱查询与后继查询
前驱
int pred(int &x,int y,int key)//查找key的前驱
{
if(x==0) return y;
if(tree[x].key<key) return pred(tree[x].right,x,key);
else return pred(tree[x].left,y,key);
}
后继
int succ(int &x,int y,int key)//查找key的后继
{
if(x==0) return y;
if(tree[x].key>key) return succ(tree[x].left,x,key);
else return succ(tree[x].right,y,key);
}
删除操作
虽说删除会使树不再平衡,但是树的深度不会增加,可以不调用maintain函数。
我们有两种删除方法。
即用前驱或后继替换这个元素。
前驱替换
int predremove(int &x,int key)
{
int kkey;
//if(!x) return 0;
--tree[x].size;
if((key==tree[x].key)||((key<tree[x].key)&&(tree[x].left==0))||((key>tree[x].key)&&(tree[x].right==0)))
{
kkey=tree[x].key;
if((tree[x].left)&&(tree[x].right))
{
tree[x].key=predremove(tree[x].left,tree[x].key+1);
}
else
{
x=tree[x].left+tree[x].right;
}
}
else if(key>tree[x].key) kkey=predremove(tree[x].right,key);
else if(key<tree[x].key) kkey=predremove(tree[x].left,key);
return kkey;
}
后继替换
int succremove(int &x,int key)
{
--tree[x].size;
if(key>tree[x].key) succremove(tree[x].right,key);
else if(key<tree[x].key) succremove(tree[x].left,key);
else
{
//有左子树,无右子树
if((tree[x].left!=0)&&(tree[x].right==0))
{
int temp=x;
x=tree[x].left;
return temp;
}
else if((tree[x].right!=0)&&(tree[x].left==0))
{
int temp=x;
x=tree[x].right;
return temp;
}
//无左子树和右子树
else if((!tree[x].left)&&(!tree[x].right))
{
int temp=x;
x=0;
return temp;
}
//有右子树
else //找到x右子树中最小元素,也就是找后继元素
{
int temp=tree[x].right;
while(tree[temp].left) temp=tree[temp].left;
tree[x].key=tree[temp].key;
succremove(tree[x].right,tree[temp].key);
}
}
}
其他查询操作
实际上几乎所有的平衡树查询都能实现。
查询最小值或最大值
int getmin(int x)//根为x的子树中的最小值
{
while(tree[x].left) x=tree[x].left;
return tree[x].key;
}
int getmax(int x)
{
while(tree[x].right) x=tree[x].right;
return tree[x].key;
}
查询第k小值
int select(int &x,int k)//求第k小数
{
int r=tree[tree[x].left].size+1;
if(r==k) return tree[x].key;
else if(r<k) return select(tree[x].right,k-r);
else return select(tree[x].left,k);
}
查询排行
int rank(int &x,int key)//求key排第几
{
if(key<tree[x].key) return rank(tree[x].left,key);
else if(key>tree[x].key) return rank(tree[x].right,key)+tree[tree[x].left].size+1;
return tree[tree[x].left].size+1;
}
最后的最后
我为了方便理解,没有打记录重复的SBT,其实就是加一个cnt嘛。
SBT其实很好写的。