AlphaGo Zero 简析
Mastering the Game of Go without Human Knowledge
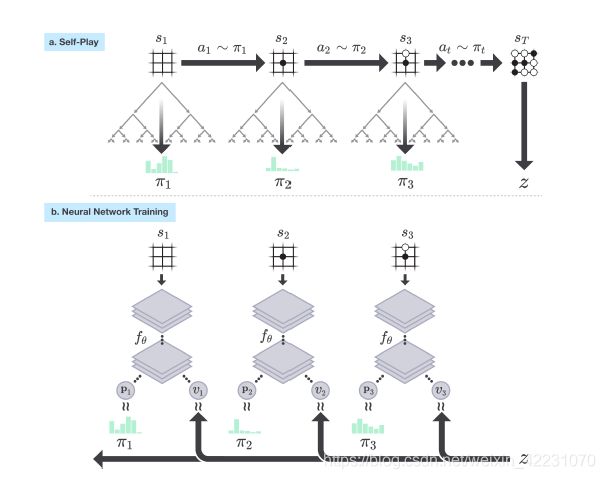
在AlphaGo Zero里,依然使用MCTS,但是去掉了每一次simulation中rollout的过程,因为这步很费时。可以看到有ab两部分,分别为自我博弈和神经网络训练。
在self-Play中,每次move都要进行一次完整的MCTS,因为对传统的MCTS进行了改进,引入edge的概念,存储Q、P、N值,用于选择节点。因为没有rollout,所以进行一次完整的MCTS速度很快。MCTS的具体步骤看下图:
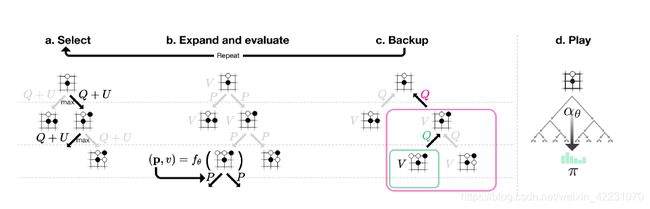
每次选择best_child的依据是 M a x ( Q ( s , a ) + U ( s , a ) ) Max(Q(s,a)+U(s,a)) Max(Q(s,a)+U(s,a)), 其中:
Q ( s , a ) = 1 / N ( s , a ) ∑ s ′ ∣ s , a → s ′ V ( s ′ ) Q(s,a)=1/N(s,a)\sum_{s'|s,a\rightarrow s'}V(s') Q(s,a)=1/N(s,a)s′∣s,a→s′∑V(s′),
U ( s , a ) ∝ P ( s , a ) / ( 1 + N ( s , a ) ) U(s,a)\propto P(s,a)/(1+N(s,a)) U(s,a)∝P(s,a)/(1+N(s,a))
Q代表Action-value,U则代表探索性,和传统的MCTS的UCT的形式很相似。
假设每次MCTS需要进行1000次simulation,结束后,MCTS返回一个概率模型 π t \pi_t πt ,其中 π t = α θ i − 1 ( s t ) ∝ N ( s , a ) 1 / t \pi_t = \alpha_{\theta_i-1}(s_t) \propto N(s,a)^{1/t} πt=αθi−1(st)∝N(s,a)1/t, 这个策略是基于MCTS的,将用于校正随机初始化的神经网络。 π t \pi_t πt是作用于第t个状态的,根据这个概率采样选择一个行动,这个和RL中的随机策略梯度是类似的。然后到T次结束,则完成一次iteration,有了结果Z,根据第一张图,这个时候就要和self-play结合起来,存储为 ( s t , π t , z t ) (s_t, \pi_t, z_t) (st,πt,zt), zt就是最后的输赢状况,每步都是一样的,+1或是-1。
( p , v ) = f θ ( s ) , L o s s = ( z − v ) 2 + π T l o g P + c ∣ ∣ θ ∣ ∣ 2 (p, v) = f_\theta(s), Loss=(z-v)^2+\pi^TlogP+c||\theta||^2 (p,v)=fθ(s),Loss=(z−v)2+πTlogP+c∣∣θ∣∣2 每一次iteration,就是一次完整的游戏过程后,对神经网络进行梯度下降。
总之,还是要看原论文,网上有些没说全很容易搞糊涂。