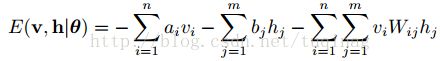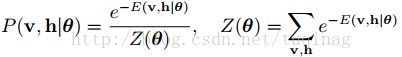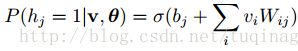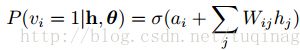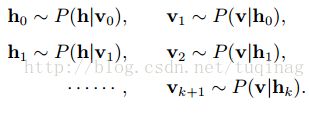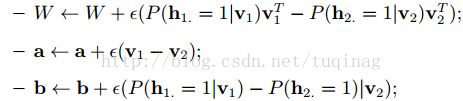Deep Learning 读书笔记（二）：关于限制玻尔兹曼机的各种
因为限制玻尔兹曼机是一个概率模型，所以会涉及到很多的概率推导，因为式子实在是过于庞大而且也不好理解，所以我也只是写出了一些会用到的结果。概率的推导实在是比较复杂，我自己其实也不能说是很懂，希望大家理解。
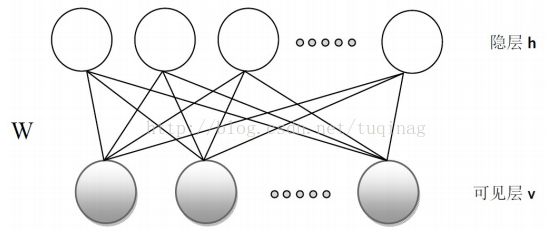
限制玻尔兹曼机（RBM）来源于玻尔兹曼机（BM），之所以被加上“限制”两字，是因为它并不允许同一层中神经元的连接。神经元的输出只有两种状态，一般使用二进制的0和1表示。限制波尔兹曼机的结构如下图所示：
RBM有一个可见层和一个隐藏层。RBM具有很好的性质：在给定可见层单元状态（输入数据）时，各隐藏层单元的激活与否是条件独立的；反之，给定隐藏层单元的状态时，可见层单元的激活与否亦条件独立。这样一来，尽管RBM所表示的分布仍无法有效计算，但通过Gibbs采样可以得到服从RBM所表示分布的随机样本。Gibbs采样的具体过程会在后面提到。
Deep Learning三大标杆之一的Bengio从理论上证明了，只要隐藏层单元的数目足够多，RBM能够拟合任意离散的分布。这一优美的性质或许也是RBM被广泛使用的原因之一。
RBM的快速学习算法----对比分歧算法是由Hinton在“A fast learning algorithm for deep belief nets”中所提出的。这篇文章表述的十分理论，充分展示了Hinton强大的数学功底，对于我来说真的有些晦涩难懂，希望以后能有机会与大家分享这篇文章。可以说是在对比分歧算法被提出之后，Deep Learning才真正有了它的用武之地，在学术界与工业界才有了如今这么好的发展。
RBM中的隐藏层单元和可见层单元可以为任意的指数族单元（给定隐藏层单元（可见层单元），可见层单元（隐藏层单元）的分布可以为任意的指数族分布），如softmax单元、高斯单元、泊松单元等。这里我们假设所有的可见层单元和隐藏层单元均为二值变量。
对于一组给定的状态（v,h），RBM作为一个系统所具备的的能量定义为：
上式中，
是RBM的参数，它们均为实数。
当参数确定时，基于该能量函数，可以得到（v,h）的联合概率分布：
由RBM的特殊结构可知：当给定可见层单元的状态时，各隐藏层的激活状态之间是条件独立的。此时，第j个隐藏层单元的激活概率为：
由于RBM的结构式对称的，当给定隐藏层单元的状态时，各可见层单元的激活状态之间也是条件独立的，即第i个可见层单元的激活概率为：
对于RBM的结构已经基本上介绍完了，接下来呢就是介绍RBM的学习算法。最常规的方法就是借助极大似然法来对参数的更新规则进行推导，但是在对极大似然函数的log形式进行推导后发现，梯度是很难计算的。因此需要使用一些采样方法来获取其的近似值，一般使用Gibbs采样法。接下来介绍下在RBM中使用Gibbs算法的具体方法。
在RBM中进行k步Gibbs采样的具体算法为：用一个训练样本（或可见层的任何随机化状态）初始化可见层的状态
，交替进行如下采样：
在采样步数k足够大的情况下，可以得到服从RBM所定义的分布的样本。
尽管利用Gibbs采样我们可以得到对数似然函数关于未知梯度的近似，但通常情况下需要使用较大的样本步数，这使得RBM的训练效率依旧不高，尤其是当观测数据的特征维度较高时。这时对比分歧算法就有了其用武之地了。
与Gibbs采样不同，对比分歧算法中，当使用训练数据初始化时，仅需要使用1步Gibbs采样便可以得到足够好的近似。在算法一开始，可见单元的状态被设置成一个训练样本，并利用公式计算隐藏层单元的二值状态。在所有隐藏层单元的状态确定后，根据公式来确定第i个可见单元
取值为1的概率，进而产生可见层的一个重构。算法的具体步骤为：
各参数的更新准则为：
要想使一个模型取得好的效果，一个好的学习算法固然不可少，当然模型参数的选择也是很重要的。接下来就针对RBM说说参数的选择中应该注意到的问题。
学习率：学习率若过大，将导致重构误差急剧增加，权值也会变得异常大。设置学习率的一般做法是先做权重更新和权重的直方图，令权重更新量为权重的10^-3倍左右。如果有一个单元的输入值很大，则权重更新应再小一些，因为同一方向上较多的小的波动很容易改变梯度的符号。相反的，对于偏置，其权重更新可以大一些。
权重和偏置的初始值：一般的，连接权重
可初始化为来自正太分布N(0,0.01)的随机数，隐藏层单元的偏置
初始化为0。对于第i个可见单元，其偏置
通常初始化为
，其中
表示训练样本中第i个特征处于激活状态所占的比率。
隐藏层单元个数：如果我们关心的主要目标是避免过拟合而不是计算复杂度，则可以先估算一下用一个好的模型描述一个数据所需要的比特数，用其乘上训练集容量。基于所得的数，选择比其低一个数量级的值作为隐藏层单元的个数。如果训练数据是高度冗余的，则可以使用更少一些的隐藏层单元。