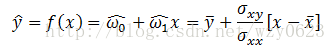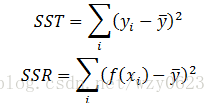MADlib——基于SQL的数据挖掘解决方案（11）——回归之线性回归
一、回归方法简介
事物之间的关系可以抽象为变量之间的关系。变量之间的关系可以分为两类：一类叫确定关系，也叫函数关系，其特征是：一个变量随着其它变量的确定而确定。另一类关系叫相关关系，变量之间的关系很难用一种精确的方法表示出来。例如，通常人的年龄越大血压越高，但人的年龄和血压之间没有确定的数量关系，人的年龄与血压之间的关系就是相关关系。回归方法就是处理变量之间相关关系的一种数学方法。其解决问题的大致步骤如下;
- 收集一组包含因变量和自变量的数据；
- 选定因变量和自变量之间的模型，即一个数学式子，利用数据按照一定规则（如最小二乘）计算模型中的系数；
- 利用统计分析方法对不同的模型进行比较，找出效果最好的模型；
- 判断得到的模型是否适合于这组数据；
- 利用模型对因变量做出预测或解释。
回归在数据挖掘中是最为基础的方法，也是应用领域和应用场景最多的方法，只要是量化型问题，我们一般都会先尝试用回归方法俩研究会分析。下面给出回归的数学定义。
令D指包含N个观测的数据集
。每个
对应于第i个观测的属性集，又称解释变量（explanatoryvariable）或自变量，而
对应于目标变量（targetvariable），或称因变量。回归任务的解释变量可以是离散的或连续的。
回归（regression）是一个任务，它学习一个把每个属性集x映射到一个输出y的目标函数（target function）f。回归的目标是找到一个可以以最小误差拟合输入数据的目标函数。回归任务的误差函数（error function）可以用绝对误差和或平方误差和表示：
二、一元线性回归
1. 最小二乘法
设Y是一个可观测的随机变量，它受到一个非随机变量因素x和随机误差ε影响。若Y与x有如下线性关系：
且ε的均值E(x)=0，方差
，其中
是固定的未知参数，称为回归系数（regression coefficient），Y称为因变量，x称为自变量，则称此Y与x之间的函数关系表达式为一元线性回归模型。利用最小二乘法可以得到回归模型参数
的最小二乘估计
，估计公式为：
其中，
。
于是就可以建立经验模型：
2. 分析回归误差
某些数据可能包含x和y的测量误差。此外，可能存在一些混杂因素影响因变量y，但未包含在模型中。正因为如此，回归任务中的因变量y可能是非确定的，也就是说，即使提供相同属性集x，它也可能产生不同的值。
我们可以使用概率方法对这类情况建模，其中y被看作一个随机变量：
测量误差和模型误差都被一个随机误差ε所吸收。通常假定数据中的随机误差出现是独立的，并且服从某种概率分布。
例如，如果随机误差来自一个均值为0、方差为
的正态分布，则
这表明最小化
蕴含地假定随机误差来自一个正态分布。此外，可以证明最能最小化这类误差的常数模型
是均值，即
。
另一种典型的误差概率模型使用拉普拉斯分布：
这表明最小化绝对误差
蕴含地假定随机误差服从拉普拉斯分布。这种情况下的最佳常量模型对应于
，y的中位数。
误差平方和的定义公式为：
线性回归的目标就是找出参数(
），它们最小化误差平方和SSE。
除SSE之外，我们还可以定义另外两种误差：
SST称为总平方和，而SSR称为回归平方和。在使用平均值估计因变量时，SST表示预测误差，而SSR代表回归模型的误差量。SST、SSE和SSR之间的关系为：SST = SSE + SSR。
3. 分析拟合的满意度
对于得到的回归方程形式，通常需要进行回归效果的评价，当有几种回归结果后，还通常需要加以比较以选出较好的方程，常用的准则有：
（1） 决定系数
，其数学定义为：
称为决定系数。显然
<=1，
大表示观测值与拟合值比较靠近，也就意味着从整体上看，n个点的散布离曲线较近。因此
大的方程为好。
（2） 剩余标准差s，其数学定义为：
s称为剩余标准差，可以将s看成是平均残差平方和的算术根，自然其值小的方程为好。其实上面两个准则所选方程总是一致的，因为s小必有残差平方和小，从而
必定大。不过，这两个量从两个角度给出我们定量的概念。
的大小给出了总体上拟合程度的好坏，s给出了观测点与回归曲线偏离的一个量值。所以，通常在实际问题中两者都求出，供使用者从不同角度去认识所拟合的曲线回归。
（3） F检验，其数学表达式为：
如果满足
，则认为变量y与x有显著的线性关系。
三、多元线性回归
设Y是一个可观测的随机变量，它受到p（p>0）个非随机变量
和随机误差ε的影响。若Y与
有如下线性关系：
其中，
是固定的未知参数，称为回归系数；ε是均值为0、方差为
的随机变量；Y称为被解释变量；
称为解释变量。此模型称为多元线性回归模型。
自变量
是非随机的且可精确观测，随机误差ε代表其随机因素对因变量Y产生的影响。对于总体
的n组观测值
，应满足式：
其中，
相互独立，且设
，记
则模型可用矩阵形式表示为：
其中，Y称为观测向量；X称为设计矩阵；ω称为待估计向量；ε是不可观测的n维随机向量，它的分量相互独立，假定
。
建立多元线性回归建模的基本步骤如下：
- 对问题进行分析，选择因变量与解释变量，作出因变量与各解释变量的散点图，初步设定线性回归模型的参数个数。
- 输入因变量与自变量的观测数据（y,X），计算参数的估计。
- 分析数据的异常点情况。
- 作显著性检验，若通过，则对模型作预测。
- 对模型进一步研究，如残差的正态性检验、残差的异方差检验、残差的自相关检验等。
四、MADlib的线性回归相关函数
1. 训练函数
（1） 语法
linregr_train( source_table,
out_table,
dependent_varname,
independent_varname,
grouping_cols,
heteroskedasticity_option
)（2） 参数
| 参数名称 |
数据类型 |
描述 |
| source_table |
VARCHAR |
包含训练数据的源表名。 |
| out_table |
VARCHAR |
包含模型的输出表名。主输出表列和概要输出表列如表2、3所示。 |
| dependent_varname |
VARCHAR |
训练数据中因变量列的名称。 |
| independent_varname |
VARCHAR |
评估使用的自变量的表达式列表，一般显式地由包括一个常数1项的自变量列表提供。 |
| grouping_cols（可选） |
VARCHAR |
缺省值为NULL。和SQL中的“GROUP BY”类似，是一个将输入数据集分成离散组的表达式，每个组运行一个回归。此值为NULL时，将不使用分组，并产生一个单一的结果模型。 |
| heteroskedasticity_option（可选） |
BOOLEAN |
缺省值为FALSE。设置成TRUE时会计算并返回模型的异方差。 |
表1 linregr_train函数参数说明
| 列名 |
数据类型 |
描述 |
| <...> |
TEXT |
当使用分组选项时，表示分组列。 |
| coef |
FLOAT8[] |
回归系数向量。 |
| r2 |
FLOAT8 |
模型确定的R平方系数。 |
| std_err |
FLOAT8[] |
系数的标准方差向量。 |
| t_stats |
FLOAT8[] |
系数的t-统计量向量。 |
| p_values |
FLOAT8[] |
系数的P值向量。 |
| odds_ratios |
FLOAT8[] |
比值比exp(ci)。 |
| condition_no |
FLOAT8 |
X*X矩阵的条件数。高条件数说明结果中的一些数值不稳定，产生的模型不可靠。这通常是由于底层设计矩阵中有相当多的共线性造成的，在这种情况下可能更适合使用其它回归技术（如弹性网络回归）。 |
| bp_stats |
FLOAT8 |
当设置了heteroskedacity参数时，表示异方差的Breush-Pagan统计。 |
| bp_p_value |
FLOAT8 |
当设置了heteroskedacity参数时，表示Breush-Pagan计算的P值。 |
| num_rows_processed |
INTEGER |
每个分组中实际使用的行数。 |
| num_missing_rows_skipped |
INTEGER |
训练时跳过的行数。如果自变量或因变量包含NULL值，则该行在每组计算时被跳过。 |
表2 linregr_train函数主输出表列说明
训练函数在产生输出表的同时，还会创建一个名为
| 列名 |
数据类型 |
描述 |
| source_table |
TEXT |
源数据表名称。 |
| out_table |
TEXT |
输出表名。 |
| dependent_varname |
TEXT |
因变量名。 |
| independent_varname |
TEXT |
自变量名。 |
| num_rows_processed |
INTEGER |
用于计算的总行数。 |
| num_missing_rows_skipped |
INTEGER |
由于空值跳过的总行数。 |
表3 linregr_train函数概要输出表列说明
2. 预测函数
（1） 语法
linregr_predict(coef, col_ind)（2） 参数
coef：FLOAT8[]类型，回归系数向量。
col_ind：FLOAT8[]类型，包含自变量列名索引的数组。
五、线性回归示例
1. 一元线性回归
（1） 问题提出
近10年来，某市社会商品零售总额与职工工资总额（单位：亿元）的数据见表4，请建立社会商品零售总额与职工工资总额数据的回归模型。
| 职工工资总额 |
23.8 |
27.6 |
31.6 |
32.4 |
33.7 |
34.9 |
43.2 |
52.8 |
63.8 |
73.4 |
| 商品零售总额 |
41.4 |
51.8 |
61.7 |
67.9 |
68.7 |
77.5 |
95.9 |
137.4 |
155.0 |
175.0 |
表4 商品零售总额与职工工资总额
该问题只有两个变量，是典型的一元回归问题，先要确定是否是线性的，当确定是线后就可以利用MADlib的线性回归函数建立它们之间的回归模型。从图1所示的数据散点图上看到，两个变量的数据的确接近一条线上，因此可以判断这些数据近似成线性关系。
图1 职工工资总额和商品零售总额关系趋势图
（2） 调用训练函数建立模型
-- 建立表并添加数据
drop table if exists t1;
create table t1 (a float, b float);
insert into t1 values
(23.8,41.4),(27.6,51.8),(31.6,61.7),(32.4,67.9),(33.7,68.7),
(34.9,77.5),(43.2,95.9),(52.8,137.4),(63.8,155.0),(73.4,175.0);
-- 训练线性模型
drop table if exists t1_linregr, t1_linregr_summary;
select madlib.linregr_train( 't1',
't1_linregr',
'b',
'array[1, a]'
);
-- 查看结果模型
\x on
select * from t1_linregr; 结果：
-[ RECORD 1 ]------------+-----------------------------------------------------------------------------
coef | {-23.5493464974992,2.79912144049615}
r2 | 0.986778045431921
std_err | {5.10282699272296,0.114555208049907}
t_stats | {-4.61496079155387,24.4346938750851}
p_values | {0.0017214811063928,8.40137971469318e-09}
condition_no | 127.169076670091
num_rows_processed | 10
num_missing_rows_skipped | 0
variance_covariance | {{26.038843317662,-0.54748720824343},{-0.54748720824343,0.0131228956913574}}从结果看，r2的值接近于1，而p_values的值足够小，说明模型较好。
（3） 利用预测函数估计残差
残差在数理统计中是指实际观察值与估计值（拟合值）之间的差。“残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话，我们可以将残差看作误差的观测值。它应符合模型的假设条件，且具有误差的一些性质。利用残差所提供的信息，来考察模型假设的合理性及数据的可靠性称为残差分析。
\x off
select a, b, predict, b - predict residual
from (select t1.*,
madlib.linregr_predict(m.coef,array[1, a]) as predict
from t1, t1_linregr m) t; 结果：
a | b | predict | residual
------+-------+------------------+---------------------
23.8 | 41.4 | 43.0697437863091 | -1.66974378630913
27.6 | 51.8 | 53.7064052601945 | -1.9064052601945
31.6 | 61.7 | 64.9028910221791 | -3.20289102217909
32.4 | 67.9 | 67.142188174576 | 0.757811825424
33.7 | 68.7 | 70.781046047221 | -2.08104604722101
34.9 | 77.5 | 74.1399917758164 | 3.36000822418363
43.2 | 95.9 | 97.3726997319344 | -1.47269973193441
52.8 | 137.4 | 124.244265560697 | 13.1557344393026
63.8 | 155 | 155.034601406155 | -0.0346014061550477
73.4 | 175 | 181.906167234918 | -6.90616723491809
(10 rows)
2. 多元线性回归
（1） 问题提出
某科学基金会希望估计从事某研究的学者的年薪Y与他们的研究成果（论文、著作等）的质量指标X1、从事研究的时间X2、能成功获得资助的指标X3之间的关系，为此按一定的实验设计方法调查了24位研究学者，得到如表5所示的数据（i为学者序号），试建立Y与X1、X2、X3之间关系的数学模型，并得出有关结论和作统计分析。
| I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| Xi1 |
3.5 |
5.3 |
5.1 |
5.8 |
4.2 |
6.0 |
6.8 |
5.5 |
3.1 |
7.2 |
4.5 |
4.9 |
| Xi2 |
9 |
20 |
18 |
33 |
31 |
13 |
25 |
30 |
5 |
47 |
25 |
11 |
| Xi3 |
6.1 |
6.4 |
7.4 |
6.7 |
7.5 |
5.9 |
6.0 |
4.0 |
5.8 |
8.3 |
5.0 |
6.4 |
| Yi |
33.2 |
40.3 |
38.7 |
46.8 |
41.4 |
37.5 |
39.0 |
40.7 |
30.1 |
52.9 |
38.2 |
31.8 |
| I |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
| Xi1 |
8.0 |
6.5 |
6.6 |
3.7 |
6.2 |
7.0 |
4.0 |
4.5 |
5.9 |
5.6 |
4.8 |
3.9 |
| Xi2 |
23 |
35 |
39 |
21 |
7 |
40 |
35 |
23 |
33 |
27 |
34 |
15 |
| Xi3 |
7.6 |
7.0 |
5.0 |
4.4 |
5.5 |
7.0 |
6.0 |
3.5 |
4.9 |
4.3 |
8.0 |
5.8 |
| Yi |
43.3 |
44.1 |
42.5 |
33.6 |
34.2 |
48.0 |
38.0 |
35.9 |
40.4 |
36.8 |
45.2 |
35.1 |
表5 从事某研究的学者的相关指标数据
该问题是典型的多元回归问题，但能否应用多元回归，最好先通过数据可视化判断它们之间的变化趋势，如果近似满足线性关系，则可以利用线性回归方法对该问题进行回归。
（2） 作出因变量Y与各自变量的样本散点图
作散点图的目的是观察因变量Y与各自变量间是否有比较好的线性关系，以便选择恰当的数学模型形式。图2分别为年薪Y与成果质量指标X1、研究工作时间X2、获得资助的指标X3之间的散点图。从图中可以看出这些点大致分布在一条直线旁边，因此有比较好的线性关系，可以采用线性回归。
图2 因变量Y与各自变量的样本散点图
（3） 调用训练函数建立模型
-- 建立表并添加数据
drop table if exists t1;
create table t1 (x1 float, x2 float, x3 float, y float);
insert into t1 values
(3.5,9,6.1,33.2), (5.3,20,6.4,40.3), (5.1,18,7.4,38.7),
(5.8,33,6.7,46.8), (4.2,31,7.5,41.4), (6.0,13,5.9,37.5),
(6.8,25,6.0,39.0), (5.5,30,4.0,40.7), (3.1,5,5.8,30.1),
(7.2,47,8.3,52.9), (4.5,25,5.0,38.2), (4.9,11,6.4,31.8),
(8.0,23,7.6,43.3), (6.5,35,7.0,44.1), (6.6,39,5.0,42.5),
(3.7,21,4.4,33.6), (6.2,7,5.5,34.2), (7.0,40,7.0,48),
(4.0,35,6.0,38.0), (4.5,23,3.5,35.9), (5.9,33,4.9,40.4),
(5.6,27,4.3,36.8), (4.8,34,8.0,45.2), (3.9,15,5.8,35.1);
-- 训练线性模型
drop table if exists t1_linregr, t1_linregr_summary;
select madlib.linregr_train( 't1',
't1_linregr',
'y',
'array[1, x1, x2, x3]'
);
-- 查看结果模型
\x on
select * from t1_linregr;结果：
-[ RECORD 1 ]------------+----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
coef | {17.4360844805194,1.11937123487486,0.321549680035209,1.33338805066807}
r2 | 0.913094894036178
std_err | {2.01313917062048,0.323340769702551,0.0365410911568227,0.294934722021009}
t_stats | {8.66114212816461,3.46189327100506,8.79967373320137,4.52095989760436}
p_values | {3.34622308123056e-08,0.00246297144041073,2.59478249724937e-08,0.000208347220434948}
condition_no | 162.923246160157
num_rows_processed | 24
num_missing_rows_skipped | 0
variance_covariance | {{4.05272932028652,-0.308664994654568,0.0010662360168379,-0.382166636046883},{-0.308664994654568,0.104549253351838,-0.00506182989810972,-0.0207961107291977},{0.0010662360168379,-0.00506182989810972,0.00133525134293122,-0.00120729338355019},{-0.382166636046883,-0.0207961107291977,-0.00120729338355019,0.0869864902536095}}从训练结果中看到，回归系数b=(17.4361,1.1194,0.3215,1.3334)，相关系数的平方r2=0.9131，t检验对应的概率p值很小。因此我们得到初步的回归方程为：
由结果对模型的判断：
- 对相关系数R的评价：本例R的绝对值为0.9556，表明线性相关性较强。
- p值检验：p<0.05（预定显著水平），说明因变量y与自变量之间有显著的线性相关关系。
两种推断方法推断的结果一致，说明因变量与自变量之间存在较强的线性关系，线性回归模型可用。
（4） 利用预测函数估计残差
\x off
select x1, x2, x3, y, predict, y - predict residual
from (select t1.*,
madlib.linregr_predict(m.coef, array[1, x1, x2, x3]) as predict
from t1, t1_linregr m) t;结果：
x1 | x2 | x3 | y | predict | residual
-----+----+-----+------+------------------+---------------------
3.5 | 9 | 6.1 | 33.2 | 32.3814980319735 | 0.818501968026474
5.3 | 20 | 6.4 | 40.3 | 38.333429150336 | 1.966570849664
5.1 | 18 | 7.4 | 38.7 | 38.7998435939587 | -0.0998435939586741
5.8 | 33 | 6.7 | 46.8 | 43.4732770234316 | 3.32672297656843
4.2 | 31 | 7.5 | 41.4 | 42.1058941280958 | -0.705894128095842
6 | 13 | 5.9 | 37.5 | 36.1994472291679 | 1.3005527708321
6.8 | 25 | 6 | 39 | 41.0868791825571 | -2.08687918255711
5.5 | 30 | 4 | 40.7 | 38.5726688760597 | 2.12733112394031
3.1 | 5 | 5.8 | 30.1 | 30.2475344026823 | -0.147534402682325
7.2 | 47 | 8.3 | 52.9 | 51.6755131538182 | 1.22448684618178
4.5 | 25 | 5 | 38.2 | 37.1789372916769 | 1.02106270832314
4.9 | 11 | 6.4 | 31.8 | 34.9917335360692 | -3.19173353606917
8 | 23 | 7.6 | 43.3 | 43.9204461854054 | -0.620446185405434
6.5 | 35 | 7 | 44.1 | 45.2999526631148 | -1.19995266311481
6.6 | 39 | 5 | 42.5 | 44.031312405407 | -1.53131240540699
3.7 | 21 | 4.4 | 33.6 | 34.1972087532353 | -0.597208753235293
6.2 | 7 | 5.5 | 34.2 | 33.9606681756644 | 0.239331824335615
7 | 40 | 7 | 48 | 47.4673866807283 | 0.532613319271704
4 | 35 | 6 | 38 | 41.1681365252596 | -3.1681365252596
4.5 | 23 | 3.5 | 35.9 | 34.5357558556043 | 1.36424414439566
5.9 | 33 | 4.9 | 40.4 | 41.1851156557165 | -0.785115655716531
5.6 | 27 | 4.3 | 36.8 | 38.119973374642 | -1.31997337464198
4.8 | 34 | 8 | 45.2 | 44.4088599344604 | 0.791140065539594
3.9 | 15 | 5.8 | 35.1 | 34.3585281909343 | 0.741471809065693
(24 rows)