【深度学习】波尔次曼机,受限波尔兹曼机,DBN详解


神经网络自20世纪50年代发展起来后,因其良好的非线性能力、泛化能力而备受关注。然而,传统的神经网络仍存在一些局限,在上个世纪90年代陷入衰落,主要有以下几个原因:
1、传统的神经网络一般都是单隐层,最多两个隐层,因为一旦神经元个数太多、隐层太多,模型的参数数量迅速增长,模型训练的时间非常之久;
2、传统的神经网络,随着层数的增加,采用随机梯度下降的话一般很难找到最优解,容易陷入局部最优解。在反向传播过程中也容易出现梯度弥散或梯度饱和的情况,导致模型结果不理想;
3、随着神经网络层数的增加,深度神经网络的模型参数很多,就要求在训练时需要有很大的标签数据,因为训练数据少的时候很难找到最优解,也就是说深度神经网络不具备解决小样本问题的能力。
由于以上的限制,深度的神经网络一度被认为是无法训练的,从而使神经网络的发展一度停滞不前。
2006年,“神经网络之父”Geoffrey Hinton祭出神器,一举解决了深层神经网络的训练问题,推动了深度学习的快速发展,开创了人工智能的新局面,使近几年来科技界涌现出了很多智能化产品,深深地影响了我们每个人的生活。
那这个神器是什么呢?那就是“深度信念网络”(Deep Belief Network,简称DBN)。
深度信念网络(DBN)通过采用逐层训练的方式,解决了深层次神经网络的优化问题,通过逐层训练为整个网络赋予了较好的初始权值,使得网络只要经过微调就可以达到最优解。而在逐层训练的时候起到最重要作用的是“受限玻尔兹曼机”(Restricted Boltzmann Machines,简称RBM),为什么叫“受限玻尔兹曼机”呢?因为还有一个是不受限的,那就是“玻尔兹曼机”(Boltzmann Machines,简称BM)。
下面依次介绍一下什么是“玻尔兹曼机”(BM)、“受限玻尔兹曼机”(RBM)?
一、玻尔兹曼机(Boltzmann Machines,简称BM)

玻尔兹曼机于1986年由大神Hinton提出,这种网络中神经元只有两种状态(未激活、激活),用二进制0、1表示,状态的取值根据概率统计法则决定。
由于这种概率统计法则的表达形式与著名统计力学家L.E.Boltzmann提出的玻尔兹曼分布类似,故将这种网络取名为“玻尔兹曼机”。
在物理学上,玻尔兹曼分布(也称为吉布斯分布,Gibbs Distribution)是描述理想气体在受保守外力的作用(或保守外力的作用不可忽略)时,处于热平衡态下的气体分子按能量的分布规律。
在统计学习中,如果我们将需要学习的模型看成高温物体,将学习的过程看成一个降温达到热平衡的过程(热平衡在物理学领域通常指温度在时间或空间上的稳定),最终模型的能量将会收敛为一个分布,在全局极小能量上下波动,这个过程称为“模拟退火”,其名字来自冶金学的专有名词“退火”,即将材料加热后再以一定的速度退火冷却,可以减少晶格中的缺陷,而模型能量收敛到的分布即为玻尔兹曼分布。
听起来很难理解的样子,只需要记住一个关键点:能量收敛到最小后,热平衡趋于稳定,也就是说,在能量最少的时候,网络最稳定,此时网络最优。
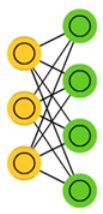
玻尔兹曼机(BM)是由随机神经元全连接组成的反馈神经网络,且对称连接,由可见层、隐层组成,BM可以看做是一个无向图,如下图所示:

其中,x1、x2、x3为可见层,x4、x5、x6为隐层。
整个能量函数定义为
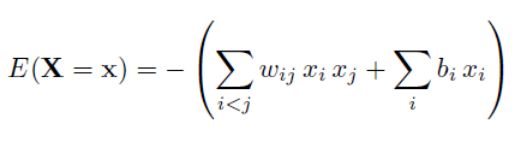
其中,w为权重,b为偏置变量,x只有{0,1}两种状态。
根据玻尔兹曼分布,给出的一个系统在特定状态能量和系统温度下的概率分布,如下:
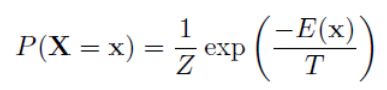
前面讲过,“能量收敛到最小后,热平衡趋于稳定”,因此:
二、受限玻尔兹曼机 Restricted BoltzmannMachine (RBM)
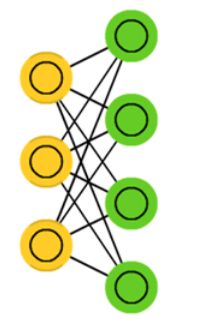
所谓“受限玻尔兹曼机”(RBM)就是对“玻尔兹曼机”(BM)进行简化,使玻尔兹曼机更容易更加简单使用,原本玻尔兹曼机的可见元和隐元之间是全连接的,而且隐元和隐元之间也是全连接的,这样就增加了计算量和计算难度。
“受限玻尔兹曼机”(RBM)同样具有一个可见层,一个隐层,但 层内无连接,层与层之间全连,节点变量仍然取值为0或1,是一个二分图。也就是将“玻尔兹曼机”(BM)的层内连接去掉,对连接进行限制,就变成了“受限玻尔兹曼机”(RBM),这样就使得计算量大大减小,使用起来也就方便了很多。如上图。
“受限玻尔兹曼机”(RBM)的特点是: 在给定可见层单元状态(输入数据)时,各隐层单元的激活条件是独立的(层内无连接),同样,在给定隐层单元状态时,可见层单元的激活条件也是独立的。
跟“玻尔兹曼机”(BM)类似,根据玻尔兹曼分布,可见层(变量为v,偏置量为a)、隐层(变量为h,偏置量为b)的概率为:

RBM的本质是非监督学习的利器,可以用于降维(隐层设置少一点)、学习提取特征(隐层输出就是特征)、自编码器(AutoEncoder)以及深度信念网络(多个RBM堆叠而成)等等。
假设有一个二部图,每一层的节点之间没有链接,一层是可视层,即输入数据层(v),一层是隐藏层(h),如果假设所有的节点都是随机二值变量节点(只能取0或者1值),同时假设全概率分布p(v,h)满足Boltzmann 分布,我们称这个模型是Restricted BoltzmannMachine (RBM)。
三、深度置信网络(Deep Belief Network)
又称深度信念网络
2006年,Hinton大神又又又出手了,提出了“深度信念网络”(DBN),并给出了该模型一个高效的学习算法,这也成了深度学习算法的主要框架,在该算法中,一个DBN模型由若干个RBM堆叠而成,训练过程由低到高逐层进行训练,如下图所示:
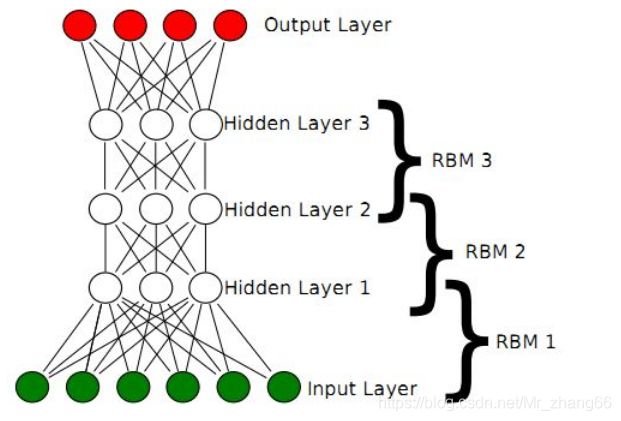
回想一下RBM,由可见层、隐层组成,显元用于接受输入,隐元用于提取特征,因此隐元也有个别名,叫特征检测器。也就是说,通过RBM训练之后,可以得到输入数据的特征。
正是由于RBM的以上特点,使得DBN逐层进行训练变得有效,通过隐层提取特征使后面层次的训练数据更加有代表性,通过可生成新数据能解决样本量不足的问题。逐层的训练过程如下:
(1)最底部RBM以原始输入数据进行训练
(2)将底部RBM抽取的特征作为顶部RBM的输入继续训练
(3)重复这个过程训练以尽可能多的RBM层

由于RBM可通过CD快速训练,于是这个框架绕过直接从整体上对DBN高度复杂的训练,而是将DBN的训练简化为对多个RBM的训练,从而简化问题。而且通过这种方式训练后,可以再通过传统的全局学习算法(如BP算法)对网络进行微调,从而使模型收敛到局部最优点,通过这种方式可高效训练出一个深层网络出来,如下图所示:

Hinton提出,这种预训练过程是一种无监督的逐层预训练的通用技术,也就是说,不是只有RBM可以堆叠成一个深度网络,其它类型的网络也可以使用相同的方法来生成网络。
参考
链接: 大话深度信念网络(DBN).