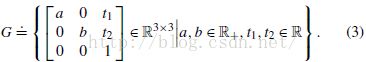TILT:Transform Invariant Low-Rank Textures

前言

淅淅沥沥的雨下了一天。一上午都没有精神，中午回宿舍睡了一个饱饱的觉，下午要沉下心来好好地写点东西，不辜负这适宜的温度。文章不太好理解，那又有什么关系呢？多花些时间就是了，真的，感受越来越强烈，有时候最慢的学习方式可能也是最快的学习方式......很多地方我也不是很理解，希望通过写博客逐字逐句地读下来加深自己的理解，同时希望博文能服务一下大众。

简介

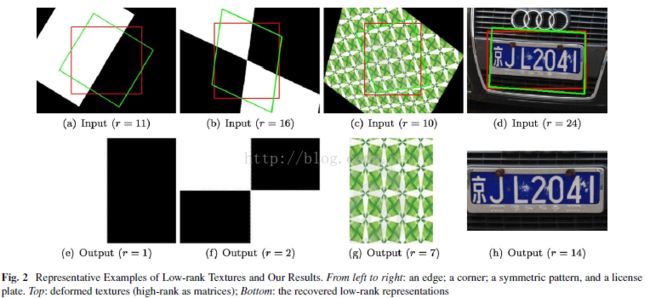
传统的图像低秩近似算法，往往仅考虑样本间像素的相似性，却没有考虑图像作为二维像素集合其本身具有的规律性。事实上，未加旋转的图像由于对称性和自相似性，可以看作是一个带噪声的低秩矩阵。当图像由端正发生旋转时，规律性被破坏矩阵的秩相应的就会增加。那么这篇文章就提出了变化不变纹理，用低秩性与噪声的稀疏性进行低秩恢复，通过几何变换把不规则的区域校正成端正的，如具有横平竖直、对称等特性，进而通过低秩来刻画这些特性。注意：这里的纹理与我们传统理解的纹理特征可能不太一样，此处的纹理指的是决定图像规则的一种低秩结构。这是一篇发表在机器视觉领域顶级期刊的文献，与以往研究工作不同的是，以往的算法经常专注于分析稀有且难以准确测量的不变量，而该文转而寻求图像中大量存在的代表结构信息的不变量，这是一个很大的不同。终极目标是，从三维平面表面上规则或近似规则的样式对应的二维图像中提取不变的信息（几何的或纹理的），这些信息可以刻画为低秩模型，如下面的例子：

红色窗口代表着原始的输入，绿色窗口则是通过我们模型校正过的纹理。可以这样理解，在绿色窗口中的图像一般都变成对称的了，因此图像具有低秩性。可以发现，校正过图像的秩要明显的低一些了。

文章的创新点是提出的方法直接使用图像感兴趣区域原始的像素点进行相应的操作，而不需要预提取如角、边、SIFT、Gabor特征等某些低层次特征，而且适用性更广，且模型及求解对破损、遮挡、杂乱等造成的严重误差也很鲁棒，只要损坏区域相对较小即可。同时，作者提供了代码可以下载，链接如下： http://perception.csl.illinois.edu/matrix-rank/tilt.html

变换不变低秩纹理

低秩纹理的定义

现在开始进入核心部分。在这篇文章中，我们将二维纹理表示为一个定义在实数二维空间上的一个函数I0(x,y)，我们称I0为低秩纹理当且仅当一维函数 张成一个有限维的线性空间，也就是有下式成立

如果r是一个有限数，我们就称I0为秩为r的纹理。容易发现，如果函数I0(x,y)的秩为1，那么函数一定是g(x).h(y)的形式。（这里我不知道该怎么解释，原文是这样说的，但是下面紧跟着给出的式子可以从分块矩阵相乘的角度进行类似理解）推广一下，一个秩为r的函数I0(x,y)可以显式地分解为r个秩为1函数的组合，即

下面几幅图像具有理想的低秩纹理

从上面可以看出，一个水平或者竖直的边(e)可以看成秩为1的纹理，一个角(f)可以看成秩为2的纹理。可以这样说，低秩纹理整合了很多传统的局部特征（边、角）。通过上述定义可以发现， 规则对称的样式(pattern)更容易形成低秩纹理。所以，低秩纹理这一概念包含了一更为宽泛的“特征”或者区域，而不仅仅局限于边角之类的。然而，需要指出的是，现实场景中并非所有的对称纹理或形状具有低秩性，我们仅考虑那些产生低秩矩阵的对称纹理。

给定一低秩纹理（对应一函数），显然将函数扩大多少倍或者对坐标进行线性变换其秩并不会发生改变，也就是说按照我们的定义，通过 变换得到的新的低秩纹理（对应一个新的函数）的与最初的低秩纹理具有相同的秩。在现实应用中，观测到的往往是变换得到的I(x,y)而希望复原原始的I0(x,y)。在本文中，无特别声明，我们认为可通过scale和transform得到彼此的两个低秩纹理等价，即 成立,这个等价群众的元素具有如下形式

公式3可理解为人工地将(x,y)拓展为(x,y,1)，1有单位截距的意味。

现实中，二维纹理图像函数并非连续的，我们通常都是离散采样将连续函数I0(x,y)表示为一个m*n的矩阵。对低秩纹理，我们总是假设采样窗口的大小显著大于纹理固有的秩，即 成立。

容易得知，只要采样率不致使由公式（2）定义的函数失真，那么得到的矩阵的秩同连续函数的秩一样。方便起见，我们将采样得到的矩阵同样记作I0(x,y)，相对其自身的维度，i0(x,y)有较低的秩。

REMARK：这里的低秩纹理与我们传统说的纹理不是一个意思，我在文章开头就提到了。

变形与损坏的低秩纹理

在大多数的真实图像中，我们很少看到完美的低秩纹理，主要有两个原因：

1.观测视角的改变引起函数域的改变；

2。纹理函数取样的值被诸如噪声、遮挡等损坏影响

为了从变形和毁坏的图像度量中提取器固有的低秩纹理，我们必须首先对影响因素建模然后设法去消除。

变形的低秩纹理

尽管许多平面表面和结构在三维中呈现出低秩纹理，但它们的图像不一定具有低秩性。假设在平面表示上有一个低秩纹理I0(i,y)，我们从特定视角观测的图像I(x,y)则是原始低秩纹理的一个转换版本，即

其中t属于一个特定的李群G（此处不作深究），我们假设G既是一个仿射群又是一个同构群。当变换得到的纹理I被视作一个矩阵的时候其不再具有低秩性。比如，理想情况下一水平边秩为1，但是当我们将其旋转45°的时候，它变成了一个满秩矩阵。

损坏的低秩纹理

除了图像域转换，观测图像的纹理还可能被噪声、遮挡等损坏。对损坏部分可以通过一个误差矩阵E来刻画，模型如下：

结果是观测矩阵I也不再低秩。在本文中，我们总是假设只有小部分被损坏，因此矩阵E是稀疏的。我们的终极目标就是从变形与损坏的纹理中精准恢复出低秩纹理I0。

问题1 复原低秩纹理

给定一变形和损坏的低秩纹理 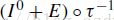，复原I0和变换t，此问题可模型化为

与RPCA模型较为相似，细节不再陈述。

通过迭代凸优化算法求解模型

通过适当的松弛模型可转化为

（ 下面内容我也不太懂）注意到尽管上面的目标函数是凸的，但是其约束是非线性的，因此整个额外难题依然是非凸的。解决该问题的一个通用的技术是在当前估计和迭代中线性化其约束条件，其线性版本为

至此变为线性问题且易于求解。论文里是这样说的，然而我并不理解这里，单纯翻译至此。求解框架也不再陈述了，原因是我自己都不懂。

就先这样吧，后面的实验结果部分反正就是效果很好了，哈哈！还望同仁阅读到此文可以发邮件至 [email protected] 多多交流，有什么自己的理解也可以和我分享，共同进步！先写到这里了。

不断更新

用低秩纹理这个性质来校正图像，直接从图像中的不变特征出发，在原始的输入图像上选取变换区域进行处理，并且在该算法的模型构建过程中，加入对噪声图像的估计和约束，使得模型对图像中少量的噪声具有鲁棒性，其校正效果也比传统的方法有很大的改善，但在出现如下两种情况时，该方法的校正结果依然是误差较大或者完全失败。一个是平面问题，当输入图像的变换区域不在同一平面时，如侧面与侧面相接、侧面和地面相接，则TILT校正失败。如下图

另一个问题是阴影问题，变换不变纹理的方法基于两个基本假设：纹理低秩和噪声稀疏。当存在较大阴影信息时，阴影信息可能会被错误地判别为纹理信息，破坏了低秩结构。如下图则不能通过TILT很好地校正

上述内容参照硕士学位论文 《建筑物外立面图像校正技术研究_李陆美》，版权归原作者所有。