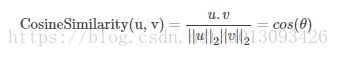词向量的优化操作
本文是基于吴恩达老师《深度学习》第五课第二周练习题所做。
0.背景简介
由于词向量的训练需要花费大量的计算,因此本文直接load预先训练好的词向量,在辅助程序中使用read_glove_vecs()函数从glove.6B.50d.txt中导入。
def read_glove_vecs(glove_file):
with open(glove_file, 'r', encoding = 'utf-8') as f:
words = set()
word_to_vec_map = {}
for line in f:
line = line.strip().split()
curr_word = line[0]
words.add(curr_word)
word_to_vec_map[curr_word] = np.array(line[1:], dtype=np.float64)
return words, word_to_vec_map文本所需的第三方库及辅助程序,可点击此处下载。
import numpy as np
from w2v_utils import *
words, word_to_vec_map = read_glove_vecs('data\glove.6B.50d.txt')其实GloVe向量集为我们提供了更多的有用的信息,首先我们来分析一下如何确定两个词之间的相似性。
1.余弦相似度
为了衡量两个向量间的相似度,我们采用余弦相似度的定义,其实质就是计算两个向量的余弦值,直观的理解就是使用向量间的夹角大小来衡量二者的相似性。计算公式及原理图如下。
def cosine_similarity(u, v):
distance = 0
dot = np.dot(u, v)
norm_u = np.sqrt(np.sum(u ** 2))
norm_v = np.sqrt(np.sum(v ** 2))
cosine_similarity = dot / (norm_u * norm_v)
return cosine_similarityfather = word_to_vec_map[b"father"]
mother = word_to_vec_map[b"mother"]
ball = word_to_vec_map[b"ball"]
crocodile = word_to_vec_map[b"crocodile"]
france = word_to_vec_map[b"france"]
italy = word_to_vec_map[b"italy"]
paris = word_to_vec_map[b"paris"]
rome = word_to_vec_map[b"rome"]
print("cosine_similarity(father, mother) = ", cosine_similarity(father, mother))
print("cosine_similarity(ball, crocodile) = ",cosine_similarity(ball, crocodile))
print("cosine_similarity(france - paris, rome - italy) = ",\
cosine_similarity(france - paris, rome - italy))cosine_similarity(father, mother) = 0.8909038442893615
cosine_similarity(ball, crocodile) = 0.2743924626137942
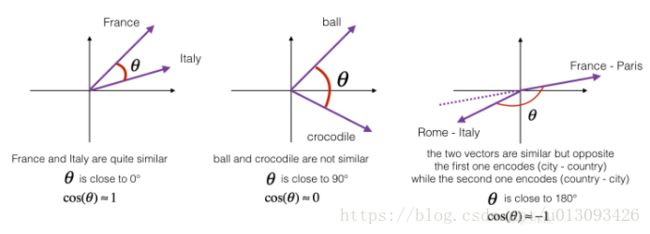
cosine_similarity(france - paris, rome - italy) = -0.67514793081742012.词类比任务
词类比任务的主要形式如下:‘man is to woman as king is to queen’ ,具体说来,我们要试图找到一个单词d,完成句子 “a is to b as c is to _为实现这个任务,我们会使用余弦相似度来计算e_b−e_a 与e_d−e_c 之间的相似度。
def complete_analogy(word_a, word_b, word_c, word_to_vec_map):
word_a, word_b, word_c = word_a.lower(), word_b.lower(), word_c.lower()
e_a, e_b, e_c = word_to_vec_map[word_a], word_to_vec_map[word_b],\
word_to_vec_map[word_c]
words = word_to_vec_map.keys()
max_cosine_sim = -100
best_word = None
for w in words:
if w in [word_a, word_b, word_c]:
continue
cosine_sim = cosine_similarity(e_b - e_a, word_to_vec_map[w] - e_c)
if cosine_sim > max_cosine_sim:
max_cosine_sim = cosine_sim
best_word = w
triads_to_try = [('italy', 'italian', 'spain'), ('india', 'delhi', 'japan'), \
('man', 'woman', 'boy'), ('small', 'smaller', 'large')]
for triad in triads_to_try:
print ('{} -> {} :: {} -> {}'.format( *triad, complete_analogy(*triad,word_to_vec_map)))italy -> italian :: spain -> spanish
india -> delhi :: japan -> tokyo
man -> woman :: boy -> girl
small -> smaller :: large -> larger3.词向量除偏
词语是包含感情色彩的,但是机器是很难体会到这其中的含义,为了避免机器学习产生歧视与偏见,我们需要在算法上加以优化。首先我们初步了解下GloVe词向量与性别具有怎样的关联。令g=e_woman - e_man,g可以代表gender(性别)的概念。当然在实际中我们会选择很多对词取多个g值的平均值作为最终的g值。
g = word_to_vec_map['woman'] - word_to_vec_map['man']
print(g)[-0.087144 0.2182 -0.40986 -0.03922 -0.1032 0.94165
-0.06042 0.32988 0.46144 -0.35962 0.31102 -0.86824
0.96006 0.01073 0.24337 0.08193 -1.02722 -0.21122
0.695044 -0.00222 0.29106 0.5053 -0.099454 0.40445
0.30181 0.1355 -0.0606 -0.07131 -0.19245 -0.06115
-0.3204 0.07165 -0.13337 -0.25068714 -0.14293 -0.224957
-0.149 0.048882 0.12191 -0.27362 -0.165476 -0.20426
0.54376 -0.271425 -0.10245 -0.32108 0.2516 -0.33455
-0.04371 0.01258 ]接下来分析不同词与g之间的余弦相似度代表的含义:
print ('List of names and their similarities with constructed vector:')
#girls and boys name
name_list = ['john', 'marie', 'sophie', 'ronaldo', 'priya', 'rahul', 'danielle', 'reza', 'katy', 'yasmin']
for w in name_list:
print (w, cosine_similarity(word_to_vec_map[w], g))
List of names and their similarities with constructed vector:
john -0.23163356145973724
marie 0.315597935396073
sophie 0.31868789859418784
ronaldo -0.31244796850329437
priya 0.17632041839009402
rahul -0.16915471039231716
danielle 0.24393299216283895
reza -0.07930429672199553
katy 0.2831068659572615
yasmin 0.23313857767928758由此可见,女性名字与g之间的余弦相似度趋近于正值,男性名字与g之间的余弦相似度趋近负值。
试一试其他值:
print('Other words and their similarities:')
word_list = ['lipstick', 'guns', 'science', 'arts', 'literature', 'warrior','doctor', 'tree', 'receptionist',
'technology', 'fashion', 'teacher', 'engineer', 'pilot', 'computer', 'singer']
for w in word_list:
print (w, cosine_similarity(word_to_vec_map[w], g))
List of names and their similarities with constructed vector:
john -0.23163356145973724
marie 0.315597935396073
sophie 0.31868789859418784
ronaldo -0.31244796850329437
priya 0.17632041839009402
rahul -0.16915471039231716
danielle 0.24393299216283895
reza -0.07930429672199553
katy 0.2831068659572615
yasmin 0.23313857767928758
Other words and their similarities:
lipstick 0.2769191625638267
guns -0.1888485567898898
science -0.06082906540929701
arts 0.008189312385880337
literature 0.06472504433459932
warrior -0.20920164641125288
doctor 0.11895289410935041
tree -0.07089399175478091
receptionist 0.33077941750593737
technology -0.13193732447554302
fashion 0.03563894625772699
teacher 0.17920923431825664
engineer -0.0803928049452407
pilot 0.0010764498991916937
computer -0.10330358873850498
singer 0.1850051813649629我们注意到computer更靠近man,而literature更靠近woman,这就是偏见问题。
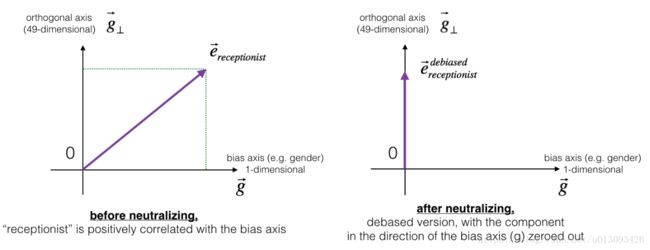
3.1中立化偏差
下图将会帮助了解中立化是如何实现的。如果使用一个50维的词向量,那么这50维的空间可以划分为两个部分:偏差方向g和其余49维g_perpendicular.中立化的过程就是让向量e_receptionist在g方向的分量为零的过程,最终获得向量![]()
def neutralize(word, g, word_to_vec_map):
e = word_to_vec_map[word]
e_biascomponent = np.dot(e, g) / np.square(np.linalg.norm(g)) * g
e_debiased = e - e_biascomponent
return e_debiasede = "receptionist"
print("cosine similarity between " + e + " and g, before neutralizing: ", cosine_similarity(word_to_vec_map["receptionist"], g))
e_debiased = neutralize("receptionist", g, word_to_vec_map)
print("cosine similarity between " + e + " and g, after neutralizing: ", cosine_similarity(e_debiased, g))
cosine similarity between receptionist and g, before neutralizing: 0.33077941750593737
cosine similarity between receptionist and g, after neutralizing: -2.099120994400013e-173.2性别相关词对的均衡方法
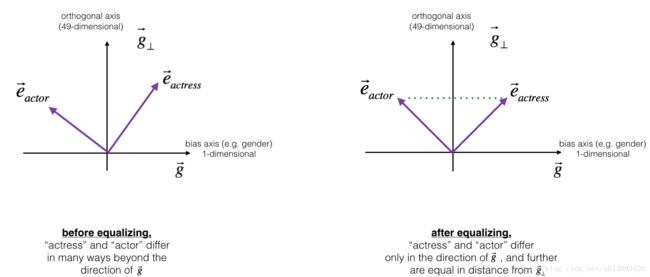
在对词向量分析的过程中,我们会发现这样的现象:actress比actor更靠近babysit,这也是偏见的一种形式。通常处理这个问题的思路是让这两个单词在g_perpendicular上的分量相等,如下图所示:
用到的公式比较多,不详述。
def equalize(pair, bias_axis, word_to_vec_map):
w1, w2 = pair
e_w1, e_w2 = word_to_vec_map[w1], word_to_vec_map[w2]
mu = (e_w1 + e_w2) / 2
mu_B = np.dot(mu, bias_axis) / np.sum(bias_axis ** 2) * bias_axis
mu_orth = mu - mu_B
e_w1B = np.dot(e_w1, bias_axis) / np.sum(bias_axis**2) * bias_axis
e_w2B = np.dot(e_w2, bias_axis) / np.sum(bias_axis**2) * bias_axis
corrected_e_w1B = np.sqrt(np.abs(1-np.sum(mu_orth**2))) * (e_w1B - mu_B)/np.linalg.norm(e_w1-mu_orth-mu_B)
corrected_e_w2B =np.sqrt(np.abs(1-np.sum(mu_orth**2))) * (e_w2B - mu_B)/np.linalg.norm(e_w2-mu_orth-mu_B)
e1 = corrected_e_w1B + mu_orth
e2 = corrected_e_w2B + mu_orth
return e1, e2print("cosine similarities before equalizing:")
print("cosine_similarity(word_to_vec_map[\"man\"], gender) = ", cosine_similarity(word_to_vec_map["man"], g))
print("cosine_similarity(word_to_vec_map[\"woman\"], gender) = ", cosine_similarity(word_to_vec_map["woman"], g))
print()
e1, e2 = equalize(("man", "woman"), g, word_to_vec_map)
print("cosine similarities after equalizing:")
print("cosine_similarity(e1, gender) = ", cosine_similarity(e1, g))
print("cosine_similarity(e2, gender) = ", cosine_similarity(e2, g))
cosine similarities before equalizing:
cosine_similarity(word_to_vec_map["man"], gender) = -0.11711095765336832
cosine_similarity(word_to_vec_map["woman"], gender) = 0.35666618846270376
cosine similarities after equalizing:
cosine_similarity(e1, gender) = -0.7004364289309387
cosine_similarity(e2, gender) = 0.7004364289309387
这些除偏的方法非常有助于减少偏见,但不能消除全部的偏见。希望读者之后进一步探索
4.参考文献
- The debiasing algorithm is from Bolukbasi et al., 2016, Man is to Computer Programmer as Woman is to
Homemaker? Debiasing Word Embeddings
- The GloVe word embeddings were due to Jeffrey Pennington, Richard Socher, and Christopher D. Manning. (https://nlp.stanford.edu/projects/glove/)