opengl 教程(11) 平移/旋转/缩放

原帖地址：http://ogldev.atspace.co.uk/www/tutorial11/tutorial11.html

      在前面的教程中，我们通过矩阵变化实现了物体在三维空间的平移、旋转、缩放操作。在本篇教程中，我们来实现这三种的变化的组合操作。通常情况下，我们会先缩放三维模型，使得它和其它物体大小相匹配，然后会旋转该物体，使得它朝向正确的方向，最后则是平移操作。为了实现上述操作，我们只需把三个变化矩阵相乘，就得到了最终的变化矩阵，该矩阵乘以顶点坐标向量，就得到变化后的坐标位置。

看下面的公式：

M_n * M_n-1 * ... * M₀ * V = (M_n* M_n-1 * ... * M₀) * V
N = M_n * M_n-1 * ... * M₀
那么
M_n * M_n-1 * ... * M₀ * V = N * V

      所以我们只需在cpu上计算组合矩阵，然后做为uniform变量，传输到shader中区。在顶点shader中，用该矩阵来乘顶点位置，得到最终的坐标。

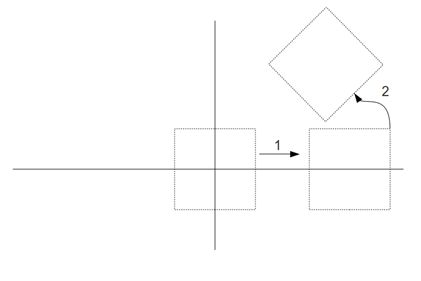
     前面说了，通常情况下，先缩放，再旋转，最后平移，矩阵相乘的方式，也是按照这个顺序，如果顺序反了或者不对，就会得到不同的结果，比如下面的图是先旋转，然后平移的效果。

下面的图则是先平移，后旋转的结果，可见顺序不同，最终的结果也不同。

      在本教程的程序中，我们引入了pipeline类，该类隐藏矩阵变化的细节，我们只要传入缩放、旋转、平移的参数，就可以得到最终的变化矩阵。

主要代码：

在math_3d.h中增加了矩阵类，主要用来实现矩阵的乘法操作。

#define ToRadian(x) ((x) * M_PI / 180.0f)
#define ToDegree(x) ((x) * 180.0f / M_PI)

首先定义了2个角度弧度转化的宏。

inline Matrix4f operator*(const Matrix4f& Right) const
{
Matrix4f Ret;
for (unsigned int i = 0 ; i < 4 ; i++) {
for (unsigned int j = 0 ; j < 4 ; j++) {
Ret.m[i][j] = m[i][0] * Right.m[0][j] +
m[i][1] * Right.m[1][j] +
m[i][2] * Right.m[2][j] +
m[i][3] * Right.m[3][j];
}
}
return Ret;
}


重载矩阵相乘操作符，实现2个4x4矩阵的乘法操作。

pipeline类抽象了单个物体矩阵变化的所有细节。

const Matrix4f* Pipeline::GetTrans()
{
Matrix4f ScaleTrans, RotateTrans, TranslationTrans;
InitScaleTransform(ScaleTrans);
InitRotateTransform(RotateTrans);
InitTranslationTransform(TranslationTrans);
m_transformation = TranslationTrans * RotateTrans * ScaleTrans;
return &m_transformation;
}
这个函数先得到三个变化矩阵，然后把它们乘起来，得到最后的矩阵。
Pipeline p;
p.Scale(sinf(Scale * 0.1f), sinf(Scale * 0.1f), sinf(Scale * 0.1f));
p.WorldPos(sinf(Scale), 0.0f, 0.0f);
p.Rotate(sinf(Scale) * 90.0f, sinf(Scale) * 90.0f, sinf(Scale) * 90.0f);
glUniformMatrix4fv(gWorldLocation, 1, GL_TRUE, (const GLfloat*)p.GetTrans());

      在渲染函数中，我们定义一个Pipeline变量，分别调用它的三个类，传入缩放、旋转、平移参数，然后得到最终的变化矩阵，并把它传送到shader中去。

     下面是程序运行后的效果，一个四面体在窗口内飞来飞去：