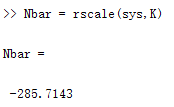控制教程 —— 介绍篇:6.状态空间控制器设计
在本教程中,我们将展示如何使用状态空间(或时域)的方法设计控制器和观测器。
本教程中使用的主要MATLAB命令为:
文章目录
-
- 形式
- 稳定性
- 可控性和可观性
- 使用极点配置设计控制器
- 介绍参考给定
- 观测器设计
形式
有几种不同的方法来描述线性微分方程组,在"控制教程 —— 介绍篇:1.建模"部分中介绍了状态空间描述。对于SISO LTI系统,状态空间形式如下:
d x d t = A x + B u \frac{d\mathbf{x}}{dt} = A\mathbf{x} + Bu dtdx=Ax+Bu y = C x + D u y = C\mathbf{x} + Du y=Cx+Du其中 x \mathbf{x} x表示系统状态变量的 n x 1 向量, u u u表示输入的量, y y y表示输出的量。矩阵 A A A (n x n), B B B (n x 1) 和 C C C (1 x n) 确定状态变量与输入和输出之间的关系。一共有 n 个一阶微分方程。状态空间描述形式也可以用于具有多输入和多输出(MIMO)的系统,这里主要关注单输入单输出(SISO)系统。
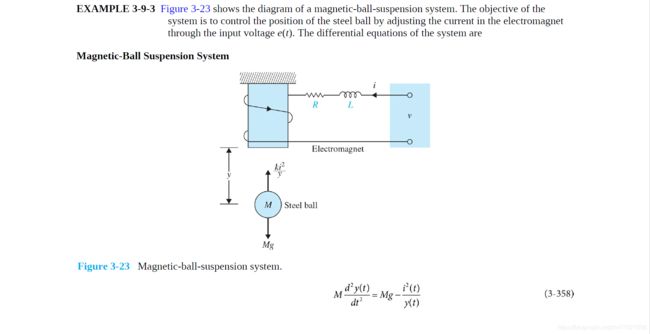
为了介绍状态空间控制设计方法,我们将以磁悬浮球为例。流过线圈的电流回产生磁力,该磁力可以平衡重力,并使球(由磁性材料制成)悬浮在空中。该系统的建模已在许多控制教科书中描述(包括B.C.Kuo撰写的《Automatic Control Systems》,第七版)。

补充参考建模方法:


也可以参考:传送门
其中 h h h 是球的垂直位置, i i i 是通过电磁铁的电流, V V V 是施加的电压, m m m 是球的质量, g g g 是重力加速度, L L L 是电感, R R R 是电阻, K K K 是施加在球上的磁力系统。为简单起见,我们将选择 m = 0.05 k g m=0.05kg m=0.05kg, K = 0.0001 K=0.0001 K=0.0001, L = 0.01 H L=0.01H L=0.01H, R = 1 Ω R=1\Omega R=1Ω, g = 9.8 m / s 2 g=9.8m/s^2 g=9.8m/s2,当 h = K i 2 / m g h=Ki^2/mg h=Ki2/mg (此时 d h / d t = 0 dh/dt = 0 dh/dt=0)时,系统处于平衡状态(球悬浮在空中),如 h = 0.01 m h=0.01m h=0.01m 时,电流约为 7 A 7A 7A,这样可以的到状态方程
d x d t = A x + B u \frac{d\mathbf{x}}{dt} = A\mathbf{x} + Bu dtdx=Ax+Bu y = C x + D u y = C\mathbf{x} + Du y=Cx+Du其中
x = [ Δ h Δ h ˙ Δ i ] x = \left[{\begin{array}{c} \Delta h \\ \Delta \dot{h} \\ \Delta i \end{array}}\right] x=⎣⎡ΔhΔh˙Δi⎦⎤是系统状态变量的集合(3x1向量), u u u 是输入电压,与平衡位置的偏差为 Δ V \Delta V ΔV, y y y是输出高度,与平衡位置的偏差为 Δ h \Delta h Δh,可以建立个系数:
A = [ 0 1 0
980 0 -2.8
0 0 -100 ];
B = [ 0
0
100 ];
C = [ 1 0 0 ];
稳定性
我们要做的第一件事就是分析开环系统(没有任何控制的情况下)的稳定性。如控制教程 —— 介绍篇:2.系统分析介绍的,根据系统矩阵 A A A 的特征值(等于传递函数的极点)来确定稳定性。 A A A 矩阵的特征值是 det ( s I − A ) = 0 \det(sI-A)=0 det(sI−A)=0关于 s s s 的解。
poles = eig(A)

从结果可以看出,有一个极点在右半平面,这意味着开环系统不稳定。
要观察初始状态为非零时,该不稳定系统的表现,可以运行一下命令:
t = 0:0.01:2;
u = zeros(size(t));
x0 = [0.01 0 0];
sys = ss(A,B,C,0);
[y,t,x] = lsim(sys,u,t,x0);
plot(t,y)
title('Open-Loop Response to Non-Zero Initial Condition')
xlabel('Time (sec)')
ylabel('Ball Position (m)')
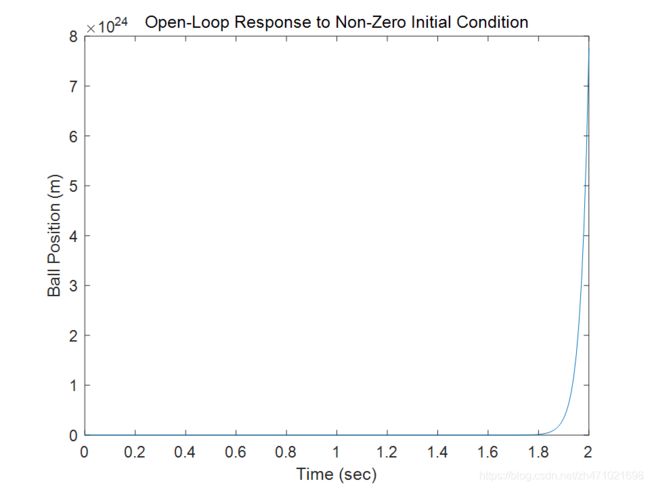
从图中可以看出球与电磁铁之间的距离回达到无穷大,但一般会掉落到桌子或者地板上。
可控性和可观性
如果始终存在一个控制输入 u ( t ) u(t) u(t),该输入可以在有限时间内将系统的任何状态转换为任何其他状态,则该系统是可控的。可以证明,当且仅当LTI系统的可控矩阵 C \mathcal{C} C 具有满秩时(例如 rank( C = n \mathcal{C}=n C=n),n 是状态变量个数)。可以使用命令rank(ctrb(A,B))或rank(ctrb(sys))。
C = [ B A B A 2 B ⋯ A n − 1 B ] \mathcal{C} = [B\ AB\ A^2B\ \cdots \ A^{n-1}B] C=[B AB A2B ⋯ An−1B]当系统存在无法直接测量状态时,必须使用可用的系统输出来估计未知部分的状态值。如果能基于系统输入 u ( t ) u(t) u(t) 和系统输出 y ( t ) y(t) y(t) 的信息确定初始状态 x ( t 0 ) x(t_0) x(t0),那么在一定的时间间隔 t 0 < t < t f t_0rank(obsv(A,C))或者rank(obsv(sys))确定。
O = [ C C A C A 2 ⋮ C A n − 1 ] \mathcal{O} = \left[ \begin{array}{c} C \\ CA \\ CA^2 \\ \vdots \\ CA^{n-1} \end{array} \right] O=⎣⎢⎢⎢⎢⎢⎡CCACA2⋮CAn−1⎦⎥⎥⎥⎥⎥⎤可控性和可观性是双重概念,当且仅当系统 ( A ′ , B ′ ) (A',B') (A′,B′) 是可观测的,系统 ( A , B ) (A,B) (A,B) 才是可控的。例如下面我们将看到的
使用极点配置设计控制器
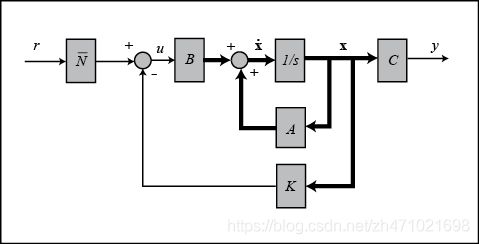
使用极点配置来构建一个控制器,全状态反馈系统的示意图如下所示,所谓全状态,是指控制器始终知道多有状态变量。对于上面的系统,我们需要一个传感器来测量球的位置,另一个传感器来测量球的速度,还需要一个传感器来测量电磁铁中的电流。
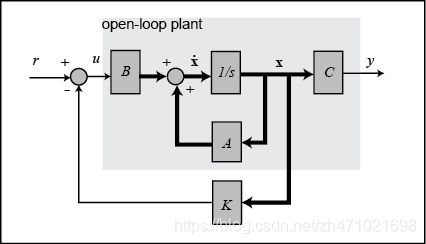
为了简单,假设参考给定为0, r r r = 0,则输入为
u = − K x u = -K\mathbf{x} u=−Kx此时,闭环反馈系统的状态空间方程为:
x ˙ = A x + B ( − K x ) = ( A − B K ) x \dot{\mathbf{x}} = A\mathbf{x} + B(-K\mathbf{x}) = (A-BK)\mathbf{x} x˙=Ax+B(−Kx)=(A−BK)x y = C x y = C\mathbf{x} y=Cx闭环反馈系统的稳定性和时域特性主要取决于矩阵特征值( A − B K A-BK A−BK)的位置,该特征值等于闭环极点。由于矩阵 A A A 和 B B B 均为 3x3,因此系统将有3个极点。通过选择适当的状态反馈增益矩阵 K K K,我们可以将这些闭环极点放置在我们想要的任何位置(因为系统是可控的)。我们可以使用MATLAB的place命令来根据闭环极点找到状态反馈增益 K K K 。
在尝试该方法之前,我们必须确定要在哪里放置闭环极点。假设控制器的标准是稳定时间<0.5s,超调<5%,那么我们可以尝试将两个主导极点放置在 -10±10i (在 ζ \zeta ζ = 0.7 或 45 度下,有 σ \sigma σ = 10 > 4.6*2)。我们可以将第三个极点放在 -50处 (这样它不会对响应产生太大的影响),我们可以稍后根据闭环行为的结果来调整它。输入如下命令
p1 = -10 + 10i;
p2 = -10 - 10i;
p3 = -50;
K = place(A,B,[p1 p2 p3]);
sys_cl = ss(A-B*K,B,C,0);
lsim(sys_cl,u,t,x0);
xlabel('Time (sec)')
ylabel('Ball Position (m)')

可以看到超调量太大(传递函数中存在零点,这将增加超调量,在状态空间中看不出明确的零点)。这里,尝试将两个极点移至更左侧,以查看瞬态响应是否有改善。
p1 = -20 + 20i;
p2 = -20 - 20i;
p3 = -100;
K = place(A,B,[p1 p2 p3]);
sys_cl = ss(A-B*K,B,C,0);
lsim(sys_cl,u,t,x0);
xlabel('Time (sec)')
ylabel('Ball Position (m)')

这次过冲减小,比较两中情况下所需的控制量 ( u u u),通常,将极点移动到越远,所需的控制量越大。
注意,如果要在同一个位置放置两个或多个极点,则place将失效,您可以使用名为acker函数,该函数可以实现相同的目标。
K = acker(A,B,[p1 p2 p3])
介绍参考给定
现在,我们将采用定义的控制系统并应用一个输入步长(我们为步长选择一个较小的值,因此可以在有效范围内保持线性化)。
t = 0:0.01:2;
u = 0.001*ones(size(t));
sys_cl = ss(A-B*K,B,C,0);
lsim(sys_cl,u,t);
xlabel('Time (sec)')
ylabel('Ball Position (m)')
axis([0 2 -4E-6 0])
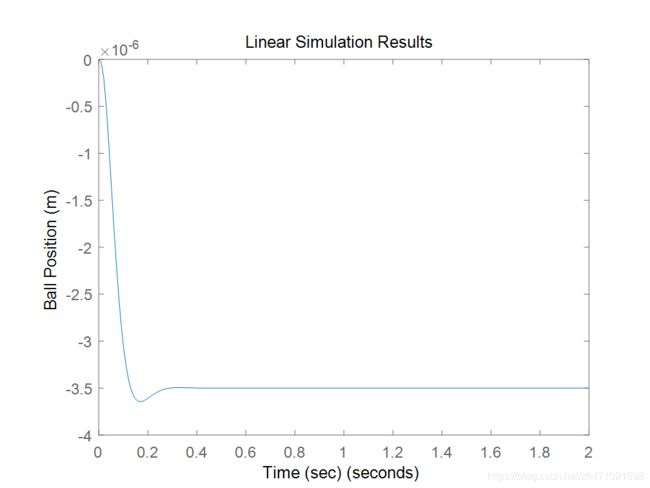
系统根本无法很好地跟踪,并且球的位置是负值而不是正。
回顾之前的示意图,我们没有将输入和参考输入进行比较;相反,我们测量所有状态,乘以增益矢量 K K K,然后从参考给定中减去该结果。这样不会使期望 K x K\mathbf{x} Kx。为了消除该问题,我们可以缩放参考输入,使其在稳态下等于 K x K\mathbf{x} Kx。下图显示了比例因子 N ‾ \overline{N} N。
我们可以在MATLAB中使用rscale来计算 N ‾ \overline{N} N(将以下命令放在K=…之后),该功能在新的版本MATLAB中已经没有,可以从这里下载。并保存在工作空间运行。
Nbar = rscale(sys,K)
lsim(sys_cl,Nbar*u,t)
title('Linear Simulation Results (with Nbar)')
xlabel('Time (sec)')
ylabel('Ball Position (m)')
axis([0 2 0 1.2*10^-3])
观测器设计
当我们无法测量所有状态变量 x \mathbf{x} x 时,我们可以构建一个观测器来估计它们,并仅测量输出 y = C x y=C\mathbf{x} y=Cx,对于悬浮球示例,我们将向系统添加三个新的估计状态变量 x ^ \hat{\mathbf{x}} x^。

观测器基本上是被控对象的复制,它具有相同的输入和几乎相同的微分方程,一个额外的项将实际测量的输出 y y y 与估计的输出 y ^ = C x ^ \hat{y} = C\hat{\mathbf{x}} y^=Cx^ 进行比较;这将有助于校正估计状态 x ^ \hat{\mathbf{x}} x^ ,并使它接近实际状态 x \mathbf{x} x 的值(如果测量结果的误差很小)。
x ^ ˙ = A x ^ + B u + L ( y − y ^ ) \dot{\hat{\mathbf{x}}} = A\hat{\mathbf{x}} + Bu + L(y - \hat{y}) x^˙=Ax^+Bu+L(y−y^) y ^ = C x ^ \hat{y} = C\hat{\mathbf{x}} y^=Cx^观测器的误差表现由 A − L C A-LC A−LC的极点决定。
e ˙ = x ˙ − x ^ ˙ = ( A − L C ) e \dot{\mathbf{e}} = \dot{\mathbf{x}} - \dot{\hat{\mathbf{x}}} = (A - LC)\mathbf{e} e˙=x˙−x^˙=(A−LC)e首先,我们需要选择观测器增益 L L L,由于我们希望观测器的动力学比系统本身快得多,因此我们需要将极点放置在距离系统主极点左侧至少5倍的位置。如果要使用place,则需要将三个观测极点放在不同位置。
op1 = -100;
op2 = -101;
op3 = -102;
由于可控性和可观性之间的对偶性,我们可以使用相同的技术来找到可控性矩阵,方法是将矩阵 B B B 替换成矩阵 C C C ,然后对每个矩阵进行转置
L = place(A',C',[op1 op2 op3])';
给出上面框图中的方程式,用于估算 x ^ \hat{\mathbf{x}} x^,并引入 e = x − x ^ \mathbf{e}=\mathbf{x}-\hat{\mathbf{x}} e=x−x^。我们将估计状态用于反馈 u = − K x ^ u=-K\hat{\mathbf{x}} u=−Kx^,因此并非所有状态变量都需要测量。
At = [ A-B*K B*K
zeros(size(A)) A-L*C ];
Bt = [ B*Nbar
zeros(size(B)) ];
Ct = [ C zeros(size(C)) ];
首先,查看当参考输入为零的系统响应, e = x \mathbf{e}=\mathbf{x} e=x
sys = ss(At,Bt,Ct,0);
lsim(sys,zeros(size(t)),t,[x0 x0]);
title('Linear Simulation Results (with observer)')
xlabel('Time (sec)')
ylabel('Ball Position (m)')

当通过 x \mathbf{x} x 和 e \mathbf{e} e 来获得 x ^ \hat{\mathbf{x}} x^ 时, x ^ = x − e \hat{\mathbf{x}} = \mathbf{x} - \mathbf{e} x^=x−e
t = 0:1E-6:0.1;
x0 = [0.01 0.5 -5];
[y,t,x] = lsim(sys,zeros(size(t)),t,[x0 x0]);
n = 3;
e = x(:,n+1:end);
x = x(:,1:n);
x_est = x - e;
% Save state variables explicitly to aid in plotting
h = x(:,1); h_dot = x(:,2); i = x(:,3);
h_est = x_est(:,1); h_dot_est = x_est(:,2); i_est = x_est(:,3);
plot(t,h,'-r',t,h_est,':r',t,h_dot,'-b',t,h_dot_est,':b',t,i,'-g',t,i_est,':g')
legend('h','h_{est}','hdot','hdot_{est}','i','i_{est}')
xlabel('Time (sec)')