PAT(甲级)2019年秋季考试
7-1 Forever (20分)
"Forever number" is a positive integer A with K digits, satisfying the following constrains:
- the sum of all the digits of A is m;
- the sum of all the digits of A+1 is n; and
- the greatest common divisor of m and n is a prime number which is greater than 2.
Now you are supposed to find these forever numbers.
Input Specification:
Each input file contains one test case. For each test case, the first line contains a positive integer N (≤5). Then N lines follow, each gives a pair of K (3 For each pair of K and m, first print in a line 思路:(1)循环是不可能循环的,公式又不会推,只有深搜这个样子。 (2)然后就是剪枝,把类似11111119这样的提前就减掉了。 (3)面向对象化,把很多小步骤写成单独的函数。 7-2 Merging Linked Lists (25分) Given two singly linked lists L1=a1→a2→⋯→an−1→an and L2=b1→b2→⋯→bm−1→bm. If n≥2m, you are supposed to reverse and merge the shorter one into the longer one to obtain a list like a1→a2→bm→a3→a4→bm−1⋯. For example, given one list being 6→7 and the other one 1→2→3→4→5, you must output 1→2→7→3→4→6→5. Each input file contains one test case. For each case, the first line contains the two addresses of the first nodes of L1 and L2, plus a positive N (≤105) which is the total number of nodes given. The address of a node is a 5-digit nonnegative integer, and NULL is represented by Then N lines follow, each describes a node in the format: where For each case, output in order the resulting linked list. Each node occupies a line, and is printed in the same format as in the input. 思路:(1)链表遍历,存入结构体数组,分出长短。 (2)正常归并操作。 7-3 Postfix Expression (25分) Given a syntax tree (binary), you are supposed to output the corresponding postfix expression, with parentheses reflecting the precedences of the operators. Each input file contains one test case. For each case, the first line gives a positive integer N (≤ 20) which is the total number of nodes in the syntax tree. Then N lines follow, each gives the information of a node (the i-th line corresponds to the i-th node) in the format: where For each case, print in a line the postfix expression, with parentheses reflecting the precedences of the operators.There must be no space between any symbols. 思路:(1)结构体存储输入,然后确定根节点。 (2)进行后序遍历(代码里写的是build),并对每个节点的信息添加括号(包括叶节点) 7-4 Dijkstra Sequence (30分) Dijkstra's algorithm is one of the very famous greedy algorithms. It is used for solving the single source shortest path problem which gives the shortest paths from one particular source vertex to all the other vertices of the given graph. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later. In this algorithm, a set contains vertices included in shortest path tree is maintained. During each step, we find one vertex which is not yet included and has a minimum distance from the source, and collect it into the set. Hence step by step an ordered sequence of vertices, let's call it Dijkstra sequence, is generated by Dijkstra's algorithm. On the other hand, for a given graph, there could be more than one Dijkstra sequence. For example, both { 5, 1, 3, 4, 2 } and { 5, 3, 1, 2, 4 } are Dijkstra sequences for the graph, where 5 is the source. Your job is to check whether a given sequence is Dijkstra sequence or not. Each input file contains one test case. For each case, the first line contains two positive integers Nv (≤103) and Ne (≤105), which are the total numbers of vertices and edges, respectively. Hence the vertices are numbered from 1 to Nv. Then Ne lines follow, each describes an edge by giving the indices of the vertices at the two ends, followed by a positive integer weight (≤100) of the edge. It is guaranteed that the given graph is connected. Finally the number of queries, K, is given as a positive integer no larger than 100, followed by K lines of sequences, each contains a permutationof the Nv vertices. It is assumed that the first vertex is the source for each sequence. All the inputs in a line are separated by a space. For each of the K sequences, print in a line 思路:(1)利用邻接矩阵存图信息。 (2)对每一组测试数据分别进行一次dij。 (3)如果利用dis选出的next节点和样例不一样,判断其已知距离是否相等, 如果相等,则按照样例来进行。 Output Specification:
Case X, where X is the case index (starts from 1). Then print n and A in the following line. The numbers must be separated by a space. If the solution is not unique, output in the ascending order of n. If still not unique, output in the ascending order of A. If there is no solution, output No Solution.Sample Input:
2
6 45
7 80
Sample Output:
Case 1
10 189999
10 279999
10 369999
10 459999
10 549999
10 639999
10 729999
10 819999
10 909999
Case 2
No Solution#includeInput Specification:
-1.Address Data Next
Address is the position of the node, Data is a positive integer no more than 105, and Next is the position of the next node. It is guaranteed that no list is empty, and the longer list is at least twice as long as the shorter one.Output Specification:
Sample Input:
00100 01000 7
02233 2 34891
00100 6 00001
34891 3 10086
01000 1 02233
00033 5 -1
10086 4 00033
00001 7 -1
Sample Output:
01000 1 02233
02233 2 00001
00001 7 34891
34891 3 10086
10086 4 00100
00100 6 00033
00033 5 -1#includeInput Specification:
data left_child right_child
data is a string of no more than 10 characters, left_child and right_child are the indices of this node's left and right children, respectively. The nodes are indexed from 1 to N. The NULL link is represented by −1. The figures 1 and 2 correspond to the samples 1 and 2, respectively.
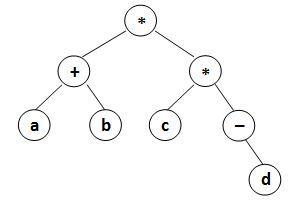
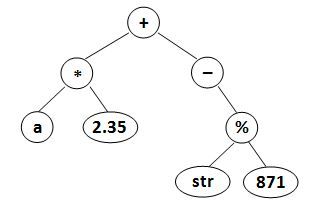
Figure 1
Figure 2
Output Specification:
Sample Input 1:
8
* 8 7
a -1 -1
* 4 1
+ 2 5
b -1 -1
d -1 -1
- -1 6
c -1 -1
Sample Output 1:
(((a)(b)+)((c)(-(d))*)*)
Sample Input 2:
8
2.35 -1 -1
* 6 1
- -1 4
% 7 8
+ 2 3
a -1 -1
str -1 -1
871 -1 -1
Sample Output 2:
(((a)(2.35)*)(-((str)(871)%))+)#includeInput Specification:
Output Specification:
Yes if it is a Dijkstra sequence, or No if not.Sample Input:
5 7
1 2 2
1 5 1
2 3 1
2 4 1
2 5 2
3 5 1
3 4 1
4
5 1 3 4 2
5 3 1 2 4
2 3 4 5 1
3 2 1 5 4
Sample Output:
Yes
Yes
Yes
No#include