并查集及其维护(C++)
基本思想
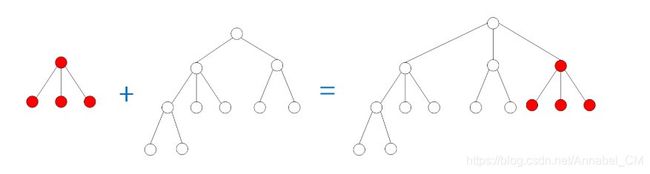
用树结构实现并查集的算法思路可以如下描述,假设现在要添加多个路径(点对):
1、初始化:每个点看做一棵树,当然这是一棵只有根节点的树,存储了这个节点本身的值作为组别(你也可以令其他不会产生冲突的记号做组别);
2、查询:对于点对(a,b),通过a和b向其根节点回溯(当然初始时就是它们本身),判断其所在组别;
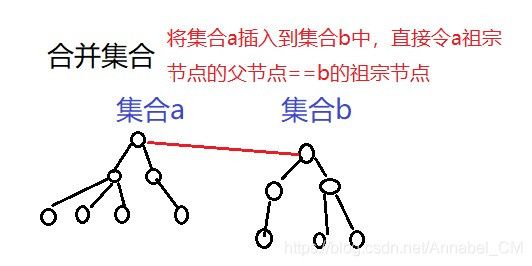
3、合并:若不在同一组别,令其中一个点(比如a吧)所在树的根节点成为另一个点(比如b)的根节点的孩子。这样即便再查询到a,通过上面的查询过程,程序也会最终判断得到的是现在b的根节点所在的组别,相当于是改变了a所在组的全部元素的组别;
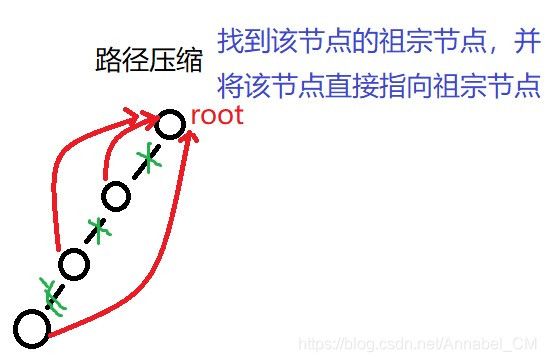
路径压缩
再看看树的生成,这一点就要在查询过程中做文章了,因为每次我们是从树的一个节点回溯到其根节点,所以一个最直接的办法是,将这条路径上的所有中间节点记录下来,全部变成根节点的子节点。但是这样一来会增加算法的空间复杂度(反复开辟内存和销毁)。所以一个备选的思路是每遍历到一个节点,就将这个节点变成他的爷爷节点的孩子(和其父节点在同一层了)。相当于是压缩了查询的路径,这样,频繁的查询当然会导致树的“扁平化”程度更彻底。
基本模板
(1)朴素并查集:
int p[N]; //存储每个点的祖宗节点(父节点)
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ ) p[i] = i;
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
(2)维护size的并查集:
int p[N], size[N];
//p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义,表示祖宗节点所在集合中的点的数量
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
size[i] = 1;
}
// 合并a和b所在的两个集合:
size[find(b)] += size[find(a)];
p[find(a)] = find(b);
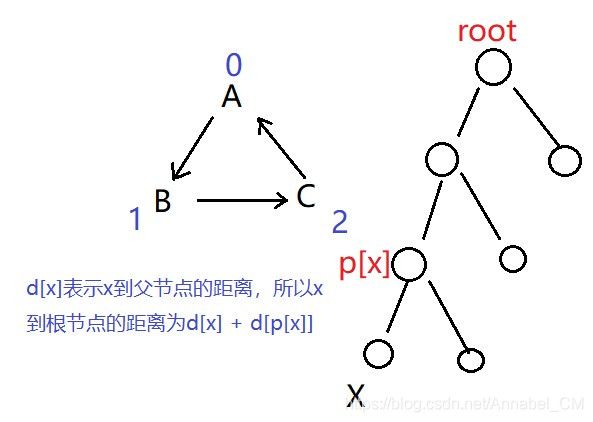
(3)维护到祖宗节点距离的并查集:
int p[N], d[N];
//p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离
// 返回x的祖宗节点
int find(int x)
{
if (p[x] != x)
{
int u = find(p[x]);
d[x] += d[p[x]];
p[x] = u;
}
return p[x];
}
// 初始化,假定节点编号是1~n
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
d[i] = 0;
}
// 合并a和b所在的两个集合:
p[find(a)] = find(b);
d[find(a)] = distance; // 根据具体问题,初始化find(a)的偏移量
作者:yxc
链接:https://www.acwing.com/blog/content/404/
来源:AcWing
经典例题
1、AcWing 836. 合并集合
一共有n个数,编号是1~n,最开始每个数各自在一个集合中。
现在要进行m个操作,操作共有两种:
“M a b”,将编号为a和b的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;
“Q a b”,询问编号为a和b的两个数是否在同一个集合中;
输入格式
第一行输入整数n和m。
接下来m行,每行包含一个操作指令,指令为“M a b”或“Q a b”中的一种。
输出格式
对于每个询问指令”Q a b”,都要输出一个结果,如果a和b在同一集合内,则输出“Yes”,否则输出“No”。
每个结果占一行。
数据范围
1≤n,m≤105
输入样例:
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例:
Yes
No
Yes
#include 2、AcWing 837. 连通块中点的数量
给定一个包含n个点(编号为1~n)的无向图,初始时图中没有边。
现在要进行m个操作,操作共有三种:
“C a b”,在点a和点b之间连一条边,a和b可能相等;
“Q1 a b”,询问点a和点b是否在同一个连通块中,a和b可能相等;
“Q2 a”,询问点a所在连通块中点的数量;
输入格式
第一行输入整数n和m。
接下来m行,每行包含一个操作指令,指令为“C a b”,“Q1 a b”或“Q2 a”中的一种。
输出格式
对于每个询问指令”Q1 a b”,如果a和b在同一个连通块中,则输出“Yes”,否则输出“No”。
对于每个询问指令“Q2 a”,输出一个整数表示点a所在连通块中点的数量
每个结果占一行。
数据范围
1≤n,m≤105
输入样例:
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例:
Yes
2
3
注意
1、cnt只有祖节点的有意义
2、要特别注意所有处理cnt的地方,都要“归根结底”
3、在点a和点b之间连一条边时,注意判断a,b 是否在同一集合内
#include 3、AcWing 240. 食物链
动物王国中有三类动物A,B,C,这三类动物的食物链构成了有趣的环形。
A吃B, B吃C,C吃A。
现有N个动物,以1-N编号。
每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述:
第一种说法是”1 X Y”,表示X和Y是同类。
第二种说法是”2 X Y”,表示X吃Y。
此人对N个动物,用上述两种说法,一句接一句地说出K句话,这K句话有的是真的,有的是假的。
当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
1) 当前的话与前面的某些真的话冲突,就是假话;
2) 当前的话中X或Y比N大,就是假话;
3) 当前的话表示X吃X,就是假话。
你的任务是根据给定的N和K句话,输出假话的总数。
输入格式
第一行是两个整数N和K,以一个空格分隔。
以下K行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中D表示说法的种类。
若D=1,则表示X和Y是同类。
若D=2,则表示X吃Y。
输出格式
只有一个整数,表示假话的数目。
数据范围
1≤N≤50000,
0≤K≤100000
输入样例:
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
输出样例:
3
思路
采用并査集,但是维护多一个数组 d,用来计算当前节点到父节点的 距离,初始化为 0(因为自身到自身的距离为 0)。根据当前节点到 root 节点的距离(root 节点只能存在一个,其他节点都是 root 节点的子节点)。这个距离算出来只能出现三种情况:0, 1, 2(距离大于或者等于3,取模处理)
//当动物x和动物y的距离%3等于1时,说明x捕食y
//当动物x和动物y的距离%3等于2时,说明y捕食x 也可以说y是x的天敌
//当动物x和动物y的距离%3等于0时,说明x和y是同类
#include