AFML读书笔记--Backtest Statistics & Understanding Strategy Risk
Advance Finance Machine Learning读书笔记
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。
因为年初疫情影响,书剩在别的地方无法出门取,AFML所以断更了很久,现在持续更新中……
之前有搜到大神weixin_38753422的AFML系列。写得很详细并且有代码和图片解释,链接在此
此系列从Part 1 Chapter 3开始写起,Chapter3之前内容可以在上面的链接里看到。(注意并不是所有内容的整理,而是我个人觉得需要整理的内容)
本文讲的时Part 3 Chapter 14 &15 Backtest Statistics & Understanding Strategy Risk
评价策略
前几章内容记录了进行回测的三种不同方法
- 前向回测法
- CPCV法
- 人造数据法
这一章主要记录的是有哪些可以给策略进行评估的指标
以下是一些指标的罗列:
- 时间跨度:我们的回测时间长度应该做到尽可能地长,囊括住所有的情况
- 平均AUM:AUM(Asset Under Management)平均持仓量, 持 仓 金 额 持 仓 标 的 物 的 数 量 \frac{持仓金额}{持仓标的物的数量} 持仓标的物的数量持仓金额
- 平均容量:最小AUM指的是能满足最基本的持仓和风险控制的需求、但是随着AUM的上升,交易成本就会不断上升,平均容量就是指该策略能达到的最优风险控制下的最大AUM
- 杠杆:这个没啥好解释的吧
- 最大持仓量:策略给出的Bet金额的最大量,建议是接近于平均AUM,给出的越大表明策略越倾向学习到了特殊事件(异常值)
- 多头仓位:在一个多空中立的策略中,多头仓位应该接近于0.5,如果偏离比较严重,回测结果可能于实际投入结果相差较远
- 交易频率:这个不解释了
- 平均持仓时间:高频策略这个值会低,低频策略这个值会高
- 年化成交量: 年 度 交 易 的 金 额 年 度 平 均 A U M \frac{年度交易的金额}{年度平均AUM} 年度平均AUM年度交易的金额
- 与指数的相关程度:如果你的收益与大盘收益的有高度相关,那么你的策略并没有多大的价值
评价指标:
- PnL:策略在回测数据上的总收益
- 多头PnL:策略的多头收益,可以用户检测策略在多空方向上的偏差
- 年化收益:不解释
- Hit比例:Bet最终是 正PnL 占总Bet数的比例
- Hit收益:在Hit bet中所产生的收益
- 策略损失:在非Hit Bet 中所产生的亏损
总收益是指变现了的或者未变现的账面收益,包括应计利息,已付息票和交易期间的股息
了解你的策略风险
每个策略都有它自己的止盈止损的点位,即使你的策略不设置止损的点位,那跌到需要交保证金的时候就是止损位了。所以一个策略总有它的两个退出位。
对称成本
假设你的策略每年会执行 n n n 个服从 I I D IID IID 的bet,那每个bet我们可以用 X i , i ∈ [ 1 , n ] X_i, i\in[1,n] Xi,i∈[1,n]来表示
正收益的bet表示为:收益 π > 0 \pi >0 π>0 机率 P [ X i = π ] = p P[X_i = \pi] = p P[Xi=π]=p
负收益的bet表示为:收益 π < 0 \pi <0 π<0 机率 P [ X i = − π ] = 1 − p P[X_i = -\pi] = 1 - p P[Xi=−π]=1−p
p p p 是模型预测的二分类结果的probability
真正例会获得正收益
假正例会负收益
真负例与假负例都会Pass,不会产生bet
因为每个bet之间都是相互独立的,所以
收益的期望是 E [ X i ] = π p + ( − π ) ( 1 − p ) = π ( 2 p − 1 ) E[X_i]=\pi p+(-\pi)(1-p)=\pi(2p-1) E[Xi]=πp+(−π)(1−p)=π(2p−1)
收益的方差是 V [ X i ] = E [ X i 2 ] − E [ X i ] 2 = 4 π 2 p ( 1 − p ) V[X_i]=E[X_i^2]-E[X_i]^2=4\pi^2 p(1-p) V[Xi]=E[Xi2]−E[Xi]2=4π2p(1−p)
也就可以算出年化夏普比率 θ \theta θ为:
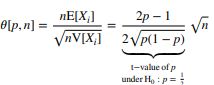
可以看出夏普比率与收益无关,并且 n n n越大,夏普比例越大,也就解释了为什么机构都喜欢高频策略了。
夏普比率是跟Precision有关,与Accuracy无关,如果Bet中负例太多, n n n就越少也就夏普比率越小。
同时,我们可以通过上式反推出 p p p的值如果我们确定夏普比率的情况下
0 ⩽ p ⩽ 1 0\leqslant p\leqslant1 0⩽p⩽1
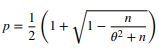
当我们策略是每周进行一bet,那么策略的precision需要达到 p = 0.6336 p = 0.6336 p=0.6336,夏普 θ \theta θ才能达到2
非对称成本
假设你的策略每年会执行 n n n 个服从 I I D IID IID 的bet,那每个bet我们可以用 X i , i ∈ [ 1 , n ] X_i, i\in[1,n] Xi,i∈[1,n]来表示
正收益的bet表示为:收益 π > 0 \pi >0 π>0 机率 P [ X i = π + ] = p i P[X_i = \pi_+] = p_i P[Xi=π+]=pi
负收益的bet表示为:收益 π < 0 \pi <0 π<0 机率 P [ X i = π − ] = 1 − p P[X_i = \pi_-] = 1 - p P[Xi=π−]=1−p
且 π + > π − \pi_+>\pi_- π+>π−
收益的期望是 E [ X i ] = ( π + − π − ) p + π i E[X_i]=(\pi_+-\pi_-)p+\pi_i E[Xi]=(π+−π−)p+πi
收益的方差是 ( π + − π − ) 2 p ( 1 − p ) (\pi_+-\pi_-)^2 p(1-p) (π+−π−)2p(1−p)
所以策划的年化夏普收益率为:
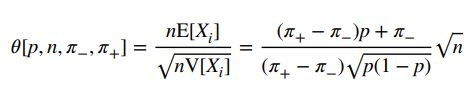
当 π + = π − \pi_+ =\pi_- π+=π−的情况下上式就是这个
![]()
到这我们就推出了在不同参数( π − , π + , n \pi_-,\pi_+,n π−,π+,n)策略需要达到多高的Precision p p p才能达成指定的夏普比率 θ \theta θ
例子:设 n = 260 , π + = . 005 , π − = − . 01 n=260, \pi_+=.005, \pi_-=-.01 n=260,π+=.005,π−=−.01, 那么要达到 θ = 2 \theta = 2 θ=2, p p p就必须达到.72(这个要达到这个Precision不容易)
同时也说明了策略在这些参数的细微变化下,会变化比较大
策略风险估计
当策略参数 n , π − , π + , θ n, \pi_-,\pi_+,\theta n,π−,π+,θ各个参数都确定了之后,就可以判断策略的临界 p p p值:
P [ p < p θ ∗ ] P[p
有一时间序列的bet记录 { π t } t = 1 , 2 … … , T \{\pi_t\}_{t=1,2……,T} { πt}t=1,2……,T
bet序列中的负收益预期可以表示为 π − = E [ { π t ∣ π t ⩽ 0 } t = 1 … … T ] \pi_-=E[\{\pi_t|\pi_t\leqslant0\}_{t=1……T}] π−=E[{ πt∣πt⩽0}t=1……T]
bet序列中的正收益预期可以表示为 π + = E [ { π t ∣ π t ⩾ 0 } t = 1 … … T ] \pi_+=E[\{\pi_t|\pi_t\geqslant 0\}_{t=1……T}] π+=E[{ πt∣πt⩾0}t=1……T]
(这里正、负收益的bet也可以通过模拟混合高斯模型,运用EF3M算法)
接下来年化bet频次 n = T y n = \frac{T}{y} n=yT y y y是运行策略的年数 1 ⩽ y ⩽ T 1 \leqslant y\leqslant T 1⩽y⩽T
最后按照下述步骤[重复采样] p p p:
重复 I I I次以下步骤:
i = 1 … … I i=1……I i=1……I
- 从时间序列bet { π t } t = 1 , 2 … … , T \{\pi_t\}_{t=1,2……,T} { πt}t=1,2……,T中抽取 ⌊ n k ⌋ \left \lfloor nk \right \rfloor ⌊nk⌋个样本 ( ⌊ . ⌋ \left \lfloor . \right \rfloor ⌊.⌋是向下取整),k是你用来衡量策略的年份(eg.k=2)。每次抽取出的样本表示为 { π j ( i ) } j = 1 … … k \{\pi_j^{(i)}\}_{j=1……k} { πj(i)}j=1……k
- 获得 p i = ∥ { π j ( i ) ∣ π j ( i ) > 0 } t = 1 … … ⌊ n k ⌋ ∥ ⌊ n k ⌋ p_i=\frac{\left \| \{\pi_j^{(i)}|\pi_j^{(i)}> 0\}_{t=1……\left \lfloor nk \right \rfloor}\right \|}{\left \lfloor nk \right \rfloor} pi=⌊nk⌋∥∥{ πj(i)∣πj(i)>0}t=1……⌊nk⌋∥∥
对 { p i } i = 1 … … I \{p_i\}_{i=1……I} { pi}i=1……I使用核密度估计方法,模拟一个PDF函数,记为 f [ p ] f[p] f[p]
在足够的多的样本抽样下,可以得出 f [ p ] ∼ N [ p ˉ , p ˉ ( 1 − p ˉ ) ] f[p] \sim N[\bar{p},\bar{p}(1-\bar{p})] f[p]∼N[pˉ,pˉ(1−pˉ)],且 p ˉ = E [ p ] = ∥ { π t ∣ π t ( i ) ⩾ 0 } t = 1 … … T ∥ T \bar{p} = E[p] = \frac{\left \| \{\pi_t|\pi_t^{(i)}\geqslant 0\}_{t=1……T} \right \|}{T} pˉ=E[p]=T∥∥{ πt∣πt(i)⩾0}t=1……T∥∥
在给予限定夏普比率 θ ∗ \theta^* θ∗情况下,策略风险可以用 P [ p < p θ ∗ ] = ∫ − ∞ p θ ∗ f [ p ] d p P[p