python可视化（2-3）绘图对象（箱线图、饼图、文字和箭头）

本文主要介绍箱线图、饼图、文字标记 和 箭头标记
涉及的接口分别为 plt.boxplot、plt.pie、plt.text、plt.arrow

本文的运行环境为 jupyter notebook
python版本为3.7

本文所用到的库包括

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

箱线图

直方图和箱线图是用以描述随机变量分布最重要的两类图，他们各有特色。本系列2.1部分对直方图已有了较为详细的介绍，今天着重介绍另一个绘图对象——箱线图。遗憾的是，作为单变量分布最为重要的两类图，他们均未被引入Excel。
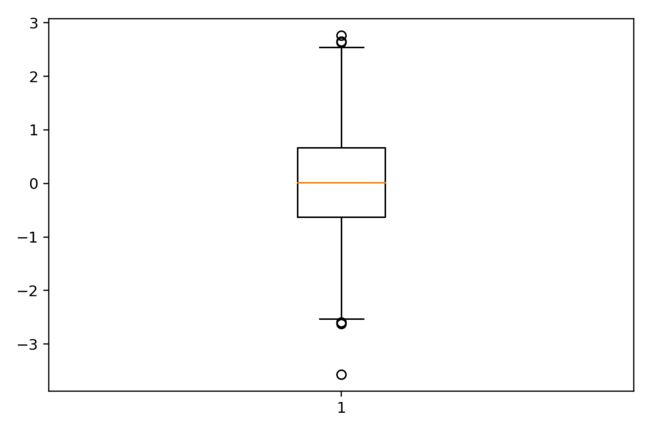
当我们拿到一个数据集，最基础也是最为重要的一步就是观察数据，对于任一随机变量，最为重要的观察点在于其聚合程度和分散程度，包括了1/4分位数，中位数，3/4分位数，上下边界分位数，离群点的箱线图，毫无疑问是该随机变量高度浓缩的一个影像，透过它，我们可以很快地知道数据全貌。

单变量分布

如图，只需要一行代码，即可将x的1000个数据浓缩到一幅图中，从下至上一共5个小横线，分别代表了x的下边界分位数，1/4分位数，中位数，3/4分位数，上下边界分位数，其中上下边界分位数通过以下公式获得：
$$上边界分位数=3/4分位数+1.5\times (3/4分位数-1/4分位数)$$
$$下边界分位数=1/4分位数-1.5\times (3/4分位数-1/4分位数)$$
超过上下边界分位数的数据均被绘制为离群点。

np.random.seed(1234)
x=np.random.randn(1000)
plt.boxplot(x)

多变量分布

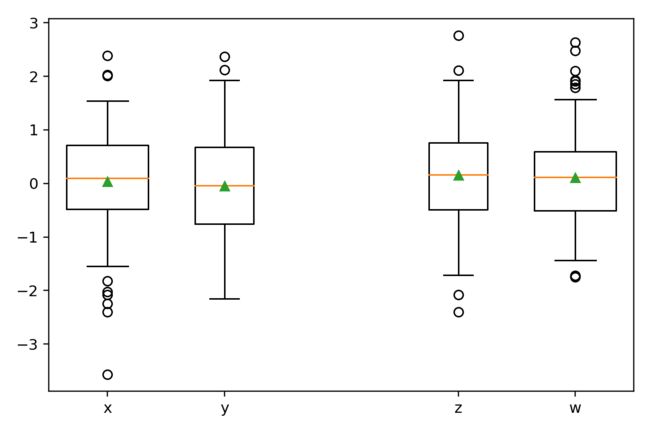
仅仅对单变量的数据分布有所了解是不够的，需要将数据集中所有变量均在同一尺度下进行展示。
在多变量分布的展示上，箱线图与直方图策略上略有不同：直方图更擅长重叠式地展示，这样可以逐一对比各序列在任一x位置的差异；箱线图更擅长将数据拉开，仅对比其在y方向上的差异。
如下图所示，x，y，z，w为四个大致相同的分布，多变量分布涉及到的修饰参数均在代码中以注释的形式予以说明。

np.random.seed(1234)
x = np.random.randn(100)
y = np.random.randn(100)
z = np.random.randn(100)
w = np.random.randn(100)
res = plt.boxplot([x, y, z, w],
                  whis=1.0,      # 确定上下边界点 Q3 + whis*IQR  whis默认为1.5
                  positions=[1, 2, 4, 5],       # 每个序列对应的x坐标位置
                  labels=['x', 'y', 'z', 'w'],    # 每个序列的x标签文本
                  widths=[0.7, 0.5, 0.5, 0.7],    # 每个序列的箱子宽度
                  showmeans=True,  # 显示均值 如图中绿色上三角
                  )

修饰

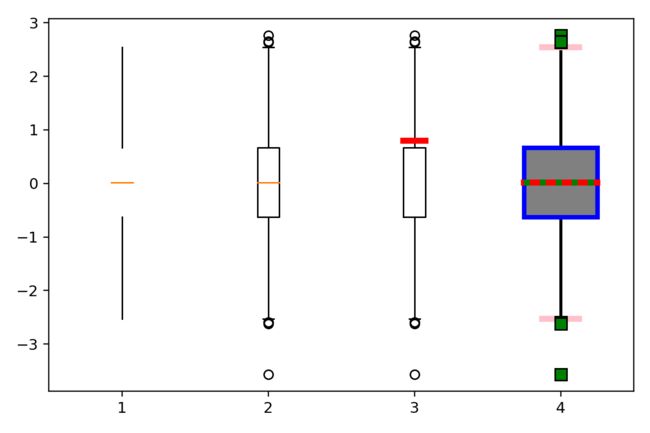
下图从左至右详细地展示了plt.boxplot接口各参数对绘图对象的影响，从图中可以看出，箱线图可供细节上调整的参数是非常多的，这给了使用者充分的自由度，用来绘制自己需要的图形，详情请看代码注释。

np.random.seed(1234)
x = np.random.randn(1000)
plt.boxplot(x,
            positions=[1],
            showcaps=False,  # 取消显示边界值线
            showbox=False,  # 取消显示箱体实体
            showfliers=False,  # 取消显示离群点
            )
# 箱线图各元素的显示
plt.boxplot(x,
            positions=[2],
            showcaps=True,  # 显示边界值线
            showbox=True,  # 显示箱体实体
            showfliers=True,  # 显示离群点
            )
# 自定义中位线
plt.boxplot(x,
                  positions=[3],
                  usermedians=[0.8],  # 自定义中位值
                  medianprops={
     'lw': 4, 'color': 'r'},  # 设置中位线
                  )
# 箱线图各元素的设置
plt.boxplot(x,
            positions=[4],
            widths=[0.5],   # 箱体宽度

            showcaps=True,  # 显示边界值线
            capprops={
     'color': 'pink', 'lw': 4, 'ls': '-'},  # 设置边界值线

            showbox=True,  # 显示箱子实体
            patch_artist=True,  # 将箱子设置成可填充样式
            boxprops={
     'facecolor': 'gray',
                      'edgecolor': 'b', 'lw': 3},  # 设置箱体填充颜色,轮廓颜色，轮廓线宽

            showfliers=True,  # 显示离群点
            flierprops={
     'marker': 's', 'markerfacecolor': 'g',
                        'markersize': 8},  # 设置离群点

            showmeans=True,  # 显示均值
            meanline=True,   # 将均值显示成一条线
            meanprops={
     'lw': 4, 'color': 'g', 'ls': ':'},  # 设置均值线

            medianprops={
     'lw': 4, 'color': 'r'},  # 设置中位线
            whiskerprops={
     'lw': 2, 'color': 'black', 'ls': '-'},  # 设置延伸线
            )

横向条形图

只需要改变一个参数vert即可将箱线图调整为横向，本例还对各序列进行了分别着色，其原理是将不同颜色传入参数boxprops中（需要注意的是，填充起作用的前提为patch_artist被设置为True）。

np.random.seed(1234)
x = np.random.normal(0,1,100)
y = np.random.normal(1,1,100)
z = np.random.normal(1,2,100)
w = np.random.normal(2,1.5,100)
for i,(data,color) in enumerate(zip([x,y,z,w],'bgrk')):
    plt.boxplot(data,
                positions=[i+1],
                widths=[0.5],
                patch_artist=True,
                boxprops=dict(lw=3,facecolor=color),
               vert=False)  # False 时为水平方向箱线图
plt.grid(axis='y')

饼图

真正的牛人，都擅长画饼
这么说，是因为很多行业、产业分析分析报告，往往都是从一张饼开始的；
是因为很多牛逼的公司，都是从一张张饼中成长起来的；
是因为很多人都是被一张张饼吸引过来的；
没有人会拒绝饼，因为世界太荒凉，每个人都很饿！

饼图数据参数

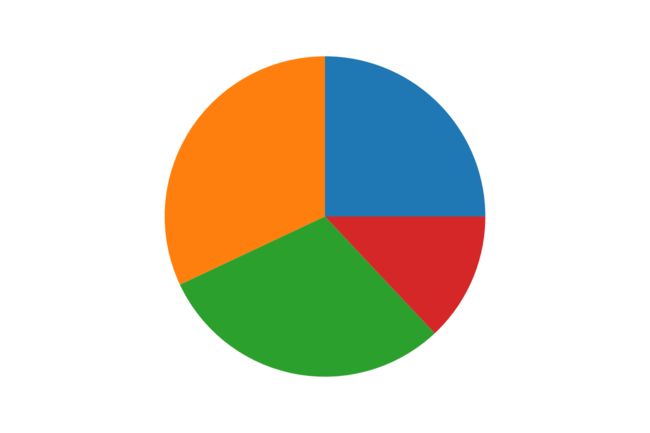
当传入的列表（元组或数据）数据和 $\ge 1$ 时，接口会自动计算各数据的占总体的百分比。

percents=[0.25,0.32,0.3,0.13]  
plt.pie(x=percents)

当传入的列表（元组或数据）数据和 $<1$ 时，接口会将不足1的部分留为空白。

percents=[0.25,0.25,0.25,0.1]  
plt.pie(x=percents)  # 若所绘制的序列所有数据和小于1，则不足1的部分，不填充色块

利用该特性，可以绘制一个只含半扇的饼图。

percents=[0.125,0.125,0.125,0.125]  # 总面积为0.5
plt.pie(x=percents) 

饼图修饰

可以通过一系列的参数修饰饼图，让饼看起来更加充实、秀色可餐。

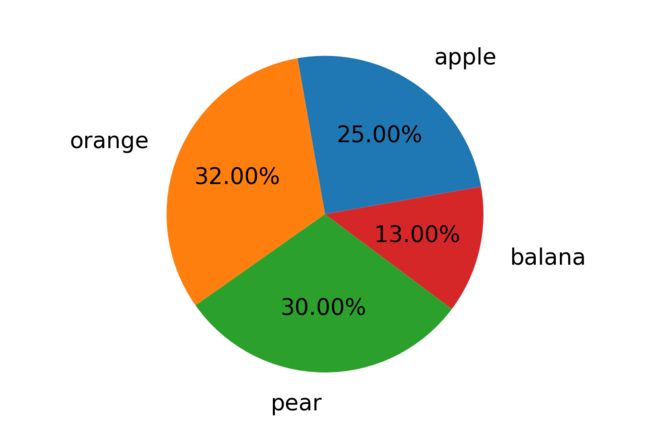
percents = [25, 32, 30, 13] #列表和大于1时，会自动转化为百分比
plt.pie(x=percents,
        labels=['apple', 'orange', 'pear', 'balana'],  # 类别标签
        textprops={
     'size': 15}, # 标签文本设置
        labeldistance=1.2, # 标签相对中心的位置
        autopct='%.2f%%', # 数据标签格式        
        startangle=10, # 第一个饼的起始角度        
        counterclock=True, #默认为逆时针，False时为顺时针
        )

当然对于比较重要的部分，可以通过参数explode将其突出显示。

percents = [25, 32, 30, 13] 
plt.pie(x=percents,
        explode=[0.2,0,0,0]
        )

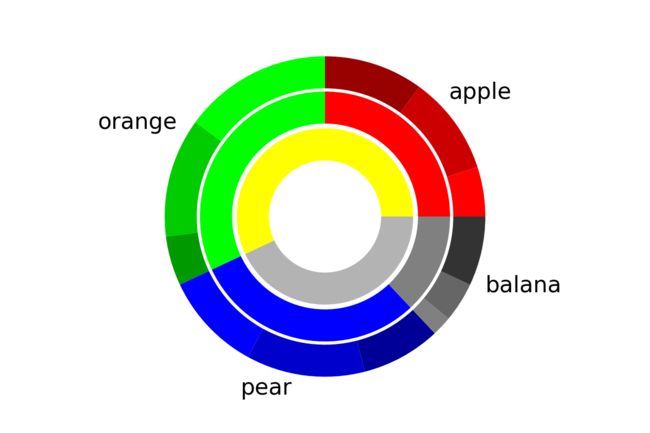
中空饼图

中空是饼图得以展现多序列分布的一种形式，如图，外圈至里圈通过颜色和区域的对应关系，呈现出一种 分 ——> 总 的美感，其原理是通过调节各系列的半径radius，宽度wedgeprops实现的。

outs=[5,10,10,
    15,12,5,
    10,12,8,
    2,4,7]
mids = [25, 32, 30, 13] 
ins = [57, 43]

plt.pie(x=outs,
        colors=[(1.0,0,0),(0.8,0,0),(0.6,0,0),
                (0,1.0,0),(0,0.8,0),(0,0.6,0),
                (0,0,1.0),(0,0,0.8),(0,0,0.6),
                (0.50,0.50,0.50),(0.40,0.40,0.40),(0.20,0.20,0.20),], # 每个pie的颜色
        radius=1.0,
        wedgeprops={
     'width':0.2}
        )

plt.pie(x=mids,
        labels=['apple', 'orange', 'pear', 'balana'],  
        textprops={
     'size': 15}, 
        labeldistance=1.4, 
        colors=[(1.0,0,0),(0,1.0,0),(0,0,1.0),(0.50,0.50,0.50),], 
        radius=0.78,
        wedgeprops={
     'width':0.2}
        )

plt.pie(x=ins,
        colors=[(1.0,1.0,0),(0.70,0.70,0.70),], 
        radius=0.55,
        wedgeprops={
     'width':0.2}
        )

目前很多dashboard控制面板，常以不完整的圈表达某一事项的完成进度，其原理相对简单，代码实现见下图。

outs = [0.8]
mids = [0.6]
ins = [0.5]

startangle=20
plt.pie(x=outs,
        startangle=startangle,
        radius=1.0,
        wedgeprops={
     'width': 0.2}
        )

plt.pie(x=mids,
        startangle=startangle,
        radius=0.78,
        wedgeprops={
     'width': 0.2}
        )

plt.pie(x=ins,
        startangle=startangle,
        radius=0.55,
        wedgeprops={
     'width': 0.2}
        )

文字标记

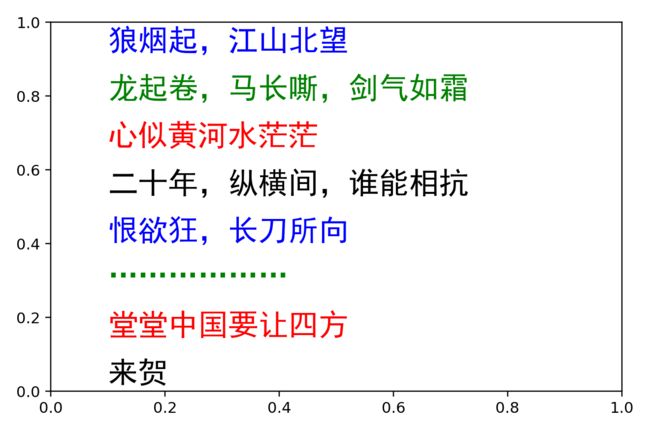
或许可视化的目的是为了少说话，文字标记接口plt.text不支持向量式地输入文字，即我们不能传入一串x，y坐标和一个文字列表，通过一行代码批量标记文字，这与matplotlib中大多数接口的设计略有不同。因此，这也是很多人用此接口常常觉得蹩脚的原因，需要for循环将每个文字标记的坐标和文字映射到绘图对象上。
以下展示了通过for循环将《精忠报国》部分歌词映射到图片上代码及输出效果，参数细节请看代码注释。

文字

geci = '''狼烟起，江山北望
龙起卷，马长嘶，剑气如霜
心似黄河水茫茫
二十年，纵横间，谁能相抗
恨欲狂，长刀所向
………………
堂堂中国要让四方
来贺'''
gecis = geci.split('\n')  # 歌词根据回车分割，返回为一行一行的歌词列表
ax = plt.figure().add_subplot(111)
ypos = np.linspace(0.95, 0.05, len(gecis))  # 每行歌词y坐标的位置
colors = 'bgrkbgrk'
for i, (geci, ypos, color) in enumerate(zip(gecis, ypos, colors)):
    plt.text(
        0.1, ypos,   # 文字坐标x，y，当接口传入transform时，此时为归一化坐标
        geci,  # 文字内容
        fontdict={
     'family': 'SimHei', 'size': 20,
                  'color': color},  # 修饰文字，此处修改了字体、字号、颜色
        va='center',  # 文本相对y的垂直位置 top，center，bottom
        ha='left',   # 文本相对x的水平位置 left，center，right
        transform=ax.transAxes,  # 归一化坐标转换
    )

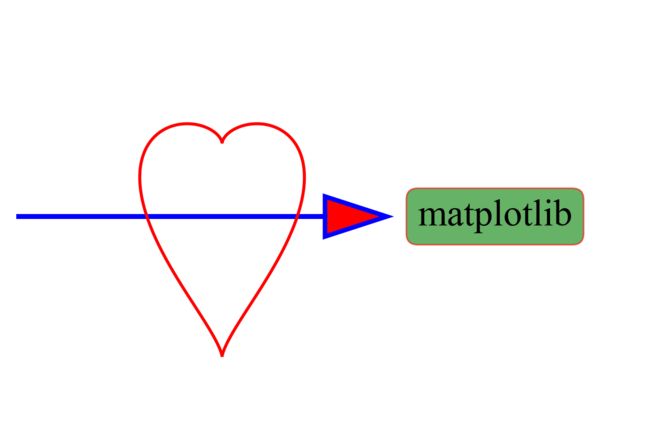
箭头标记

箭头plt.arrow与文字接口有诸多相似之处，以下代码展示了箭头接口的使用，具体内容详见代码注释。

ax = plt.figure().add_subplot(111)

plt.text(
    0.65, 0.5,
    'matplotlib',
    fontdict={
     'family': 'Times New Roman', 'size': 25},
    va='center',
    ha='left',
    transform=ax.transAxes,
    bbox={
                          # 文本边框的设置
        'boxstyle': 'round',    # 边框为圆角
        'facecolor': 'green',   # 边框内部填充绿色
        'edgecolor': 'red',     # 边框轮廓线为红色
        'alpha': 0.6,           # 边框填充色透明度为0.6
    },
)

plt.arrow(x=0, y=0.5,  # 箭头横线起始点坐标x，y，当接口传入transform时，此时为归一化坐标
          dx=0.5, dy=0,  # 箭头相对起始点，x轴与y轴的偏移
          lw=3,  # 线宽
          head_width=0.1,  # 三角形实体箭头的相对宽度
          head_length=0.1,  # 三角形实体箭头的相对长度
          edgecolor='b',  # 箭头轮廓线颜色
          facecolor='r',  # 箭头填充色
          transform=ax.transAxes,  # 归一化坐标转换
          )
plt.axis('off')

# 绘制心形线
t = np.linspace(0, np.pi, 1000)
x = np.sin(t)-0.6
y = np.cos(t) + np.power(x, 2.0/3)-0.25
plt.plot(x, y, color='red', linewidth=2, label='h')
plt.plot(-x, y, color='red', linewidth=2, label='-h')

plt.xlim((-1, 2))
plt.ylim((-1.5, 1.5))

plt.tight_layout()

总体来说，本文涉及的绘图对象重在内涵，希望对你有所启发和帮助！