网络结构搜索之梯度可微

前面介绍了强化学习方法，但屠龙刀毕竟不是人人有。梯度可微算法在保证精度可接受的前提下大幅缩短了训练周期，开启了网络结构搜索的平民化浪潮。

MobileNetV2

FBNet

ShiftNet

Gumbel-Softmax

SNAS

DARTS

ProxylessNAS

P-DARTS

PC-DARTS

DenseNAS

DARTS

DARTS 由 CMU 和 DeepMind 提出，最终发表在 ICLR 2019上。DARTS 在有限资源条件下将模型精度提升到可接受的程度，而且开放代码（quark0/darts）。可谓 NAS 领域内的一大贡献。美中不足的是代码仅在单 GPU 下搜索，以至于后续的 chenxin061/pdarts 和 yuhuixu1993/PC-DARTS 亦维持此设置，成为扩展的阻碍。

DARTS 将搜索空间放宽为连续的，以便可以通过梯度下降来优化体系结构的验证集性能。在所有混合操作中联合学习架构 $\alpha$ 和权重 $w$。这意味着一个双层优化问题，其中 $\alpha$ 作为上层变量，$w$ 作为下层变量：
$$\begin{array}{rl}\underset{\alpha }{\min }& {\mathcal{L}}_{val}(w^{\ast }(\alpha ),\alpha )\\ \text{s.t.}& w^{\ast }(\alpha )={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}_w{\mathcal{L}}_{train}(w,\alpha )\end{array}$$
DARTS 求结构梯度的近似解：

$$\begin{array}{rl}& {\nabla }_{\alpha }{\mathcal{L}}_{val}(w^{\ast }(\alpha ),\alpha )\\ \approx & {\nabla }_{\alpha }{\mathcal{L}}_{val}(w-\xi {\nabla }_w{\mathcal{L}}_{train}(w,\alpha ),\alpha )\end{array}$$

其中 $w$ 表示算法维护的当前权重，$\xi$ 是内部优化步骤的学习率。思路是通过仅使用单个训练步骤来调整 $w$ 来近似 $w^{\ast }(\alpha )$，而不是训练至收敛来完全求解内部优化。

从形式上讲，DARTS 将搜索网络分解为若干（$L$）个的单元（cell）。每个单元组织为具有 $N$ 个节点的有向无环图（DAG），其中每个节点定义一个网络层。预定义操作空间 $\mathcal{O}$，其中每个元素 $o\left(\cdot \right)$ 是在网络层执行的固定操作（例如，identity connection, and $3\times 3$ convolution）。在单元内，目标是从 $\mathcal{O}$ 中选择一个操作来连接每对节点。设一对节点为 $\left(i,j\right)$，其中 $0⩽i<j⩽N-1$，DARTS 的核心思想是将从 $i$ 传播到 $j$ 的信息表示为 $\left|\mathcal{O}\right|$ 操作的加权和，即 $f_{i,j}\left({\mathbf{x}}_i\right)={\sum }_{o\in \mathcal{O}}\frac{\exp \left\{{\alpha }_{i,j}^o\right\}}{{\sum }_{o^{\prime }\in \mathcal{O}}\exp \left\{{\alpha }_{i,j}^{o^{\prime }}\right\}}\cdot o\left({\mathbf{x}}_i\right)$，其中 ${\mathbf{x}}_i$ 是第 $i$ 个节点的输出，${\alpha }_{i,j}^o$ 是加权操作的超参数 $o\left({\mathbf{x}}_i\right)$。节点的输出是所有输入流的总和，即 ${\mathbf{x}}_j={\sum }_{i<j}{f}_{i,j}\left({\mathbf{x}}_i\right)$，整个单元格的输出是通过连接节点 ${\mathbf{x}}_2$–${\mathbf{x}}_{N-1}$ 的输出而形成的，即 $\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left({\mathbf{x}}_2,{\mathbf{x}}_3,\dots ,{\mathbf{x}}_{N-1}\right)$ 。请注意，前两个节点 ${\mathbf{x}}_0$ 和 ${\mathbf{x}}_1$ 是单元的输入节点，在架构搜索期间是固定的。

搜索过程完成后，在每个边 $\left(i,j\right)$ 上，保留具有最大 ${\alpha }_{i,j}^o$ 值的操作 $o$，并且每个节点 $j$ 连接到具有最大 ${\alpha }_{i,j}^o$ 的两个先例（$i<j$）。

实验中， 在 CIFAR-10 上搜索基础单元，由组件构建网络从头训练得到 ImageNet 上的结果。

DARTS 在 $\mathcal{O}$ 中包括以下操作：

• 3 × 3 separable convolution
• 5 × 5 separable convolution
• 3 × 3 dilated separable convolution
• 5 × 5 dilated separable convolution
• 3 × 3 max pooling
• 3 × 3 average pooling
• identity
• $zero$。

所有操作步长为1（如果适用），填充卷积特征图以保持其空间分辨率。使用 ReLU-Conv-BN 顺序进行卷积运算，并且每个可分离卷积总是应用两次（[NASNet] [AmoebaNet][PNAS]）。

卷积单元由 $N=7$ 个节点组成，其中定义输出节点为所有中间节点（不包括输入节点）的深度级联。其余的设置遵循 [NASNet] [AmoebaNet][PNAS]，然后通过将多个单元堆叠在一起形成网络。单元 $k$ 的第一和第二节点分别设置为等于单元 $k-2$ 和单元 $k-1$ 的输出，并且根据需要插入 $1\times 1$ 卷积。 位于网络总深度的1/3和2/3处的单元是约简单元，其中与输入节点相邻的所有操作步长为2。因此，体系结构编码是 $({\alpha }_{normal},{\alpha }_{reduce})$，其中 ${\alpha }_{normal}$ 由所有正常单元共享，${\alpha }_{reduce}$ 由所有约简单元共享。

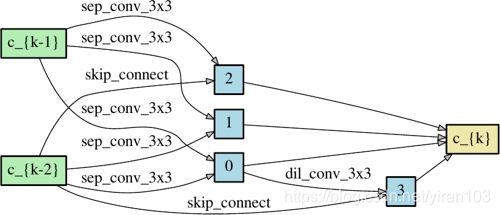
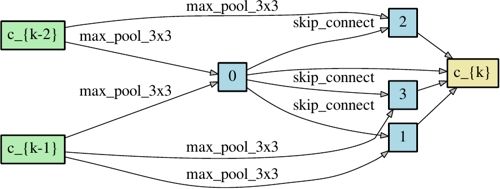
为了更好地理解深度对架构搜索的影响，DARTS 通过将堆栈中的单元数量从8增加到20来对 CIFAR-10进行架构搜索。由于单个 GPU 显存的限制，初始通道数量从16减少到6。测试误差，略低于较浅网络。

P-DARTS

P-DARTS 是同济大学和华为诺亚方舟实验室提出的一种渐进式的可微分网络结构搜索方法，致力于提升 DARTS 的迁移性能。在 CIFAR10和 CIFAR100数据集上搜索基本单元，单个P100 GPU上只需要7个小时。在DARTS中，网络结构搜索是在一个拥有8个 cell 的搜索网络上进行的，然而却是在一个拥有20个 cell 的网络上测试的，在搜索网络和测试网络之间有一个很大的深度差异。

• P-DARTS 渐进地增加搜索网络深度。P-DARTS 提出搜索空间近似，划分学习阶段，减少候选操作的种类的同时增加深度，从而降低显存和时间消耗。算法能够在16 GB 显存的 GPU 上运行。
• 上一阶段结尾将一些操作从搜索空间中删去，因此需要从头开始训练网络参数和结构参数。但是训练一个更深的网络往往比训练一个较浅的网络更难。信息往往倾向于通过 skip-connect 流动，而不是卷积。作者提出搜索空间正则，在 skip-connect 操作添加操作层面的 Dropout 来防止其过拟合到 skip-connect 上，同时限制最终结构中的 skip-connect 操作数量来进一步提高稳定性。
• 作者同时观察到测试时的识别准确率与搜索到的结构中的 skip-connect 操作数量与最终性能高度相关。因此，作者提出第二个搜索空间正则方法，即在最终生成的网络结构中，保留固定数量的 skip-connect 操作。具体的，作者根据最终阶段的结构参数，只保留权值最大的 M 个 skip-connect 操作，这一正则方法保证了搜索过程的稳定性。在本文中， M=2 。

P-DARTS 能够在 16 GB 显存的 GPU 上完成搜索。

PC-DARTS

DARTS 将操作选择转换为固定操作集的加权组合，为寻找有效的网络架构提供了快速解决方案。但联合训练超网络和搜索最优结构，内存和计算开销很大。P-DARTS 减少搜索空间，而这一近似会导致可能牺牲已发现架构的最优性。PC-DARTS 通过对超网络的一小部分进行采样以减少网络空间中的冗余，从而在不损害性能的情况下提高搜索效率。具体来说，PC-DARTS 在通道子集中执行操作搜索，并保持其他部分不变。采样不同通道可能造成在选择超网络的边时出现不一致。PC-DARTS 通过引入边正则（edge normalization）来解决这个问题，在搜索过程中添加了一组新的边级超参数，以减少搜索中的不确定性。项目地址为：yuhuixu1993/PC-DARTS。

PC-DARTS 即部分连接 DARTS，核心思想是直观的：随机抽取其中的一个子集进行操作选择，同时直接放过其余部分，而不是将所有通道都送到操作选择块中。PC-DARTS 假设该子集的计算能近似替代所有通道。除了内存和计算成本都大大降低之外，采样带来了另一个好处，即操作搜索正则化，不易陷入局部最优。然而，PC-DARTS 也带来了副作用，即网络连接的选择将变得不稳定，因为在迭代中会采样不同的信道子集。因此，PC-DARTS 引入边正则（edge normalization）来通过显式学习一组额外的边选择超参数来稳定对网络连接的搜索。通过在整个训练过程中共享这些超参数，所学习的网络结构不易受迭代中通道采样的影响，因此更加稳定。

得益于部分连接策略，PC-DARTS 能够相应地增加批量大小。在实践中，PC-DARTS 为每个操作选择随机抽取 $1/K$ 的通道，这将减少几乎 $K$ 倍的内存成本。这使得我们可以在搜索过程中使用 $K\times$ 批量大小，不仅可以将搜索速度加快 $K$ 倍，而且还稳定了搜索，特别是对于大型数据集。

当然，以上都是作者观点。读代码的话会发现通道不是随机取的，而是固定取前 $1/K$。所以“边正则”概念就有点飘了。DARTS 不仅仅选择操作，还会像剪枝一样确定连接。然而同层会有多个 softmax 输出，从中选最大显得不甚合理。额外加一组结构参数应该可以改善这一点。

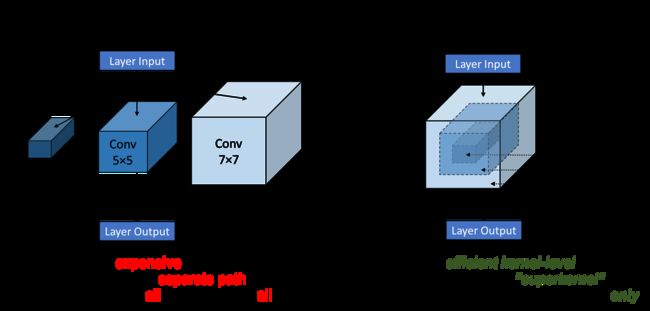
DARTS 的缺点在于其内存效率低下。为了适应 $|\mathcal{O}|$ 操作，在搜索架构的主要部分中，$|\mathcal{O}|$ 操作副本及其输出需要存储在每个节点（即每个网络层），导致 $|\mathcal{O}|\times$ 次内存使用。要装进GPU，必须在搜索期间减小批量大小，这不可避免地降低搜索速度，并且较小的批量大小可能降低搜索稳定性和准确性。

或者，内存效率的另一种解决方案是部分通道连接，如下图所示。以 ${\mathbf{x}}_i$ 与 ${\mathbf{x}}_j$ 的连接为例。这涉及定义一个通道采样掩码 ${\mathbf{S}}_{i,j}$，它为所选通道分配 $1$，为屏蔽的通道分配 $0$。所选通道送入 $\left|\mathcal{O}\right|$ 混合操作计算，而屏蔽通道则绕过这些操作，即直接复制到输出，

$$f_{i,j}^{\mathrm{P}\mathrm{C}}\left({\mathbf{x}}_i;{\mathbf{S}}_{i,j}\right)=\sum _{o\in \mathcal{O}}\frac{\exp \left\{{\alpha }_{i,j}^o\right\}}{{\sum }_{o^{\prime }\in \mathcal{O}}\exp \left\{{\alpha }_{i,j}^{o^{\prime }}\right\}}\cdot o\left({\mathbf{S}}_{i,j}\ast {\mathbf{x}}_i\right)+\left(1-{\mathbf{S}}_{i,j}\right)\ast {\mathbf{x}}_i.$$
其中，${\mathbf{S}}_{i,j}\ast {\mathbf{x}}_i$ 和 $\left(1-{\mathbf{S}}_{i,j}\right)\ast {\mathbf{x}}_i$ 分别表示选定和屏蔽的通道。

在实践中，PC-DARTS 将 $K$ 视为超参数，设置选中通道的比例为 $1/K$。 通过改变 $K$，可以在架构搜索准确度（较小的 $K$）和效率（较大的 $K$）之间进行权衡以取得平衡。

$K$ 带来的直接好处是 $f_{i,j}^{\mathrm{P}\mathrm{C}}\left({\mathbf{x}}_i;{\mathbf{S}}_{i,j}\right)$ 计算减少 $K$ 次。这允许使用更大的批量大小进行结构搜索。随即有两方面的好处：

• 首先，计算成本也可以减少 $K$ 倍。
• 此外，较大的批量大小意味着可以在每次迭代期间对更多训练数据进行采样。这对于结构搜索尤为重要。在大多数情况下，一个操作相对于另一个操作的优势并不显著，除非在一个小批量中包含更多的训练数据，以减少更新网络权重和架构参数的不确定性。

通道采样对神经架构搜索的影响既有有积极的也有消极的：

• 在好的一面，为混合操作输入一小部分通道，同时保持其余部分不变，可以减少在选择操作时的偏向。换句话说，对于边 $\left(i,j\right)$，给定输入 ${\mathbf{x}}_i$，使用两组超参数 $\left\{{\alpha }_{i,j}^o\right\}$ 和 $\left\{{\alpha }_{i,j}^{\prime o}\right\}$ 的差别大大减少了，因为只有一小部分（$1/K$）的输入通道将通过混合操作，而其余通道保持不变。这削弱了 $\mathcal{O}$ 中无参数操作（如 skip-connect、max-pooling 等）相对于含参操作（例如各种卷积）的优势。在早期阶段，搜索算法通常更青睐无参操作，因为它们没有训练参数，从而产生更一致的输出，即 $o\left({\mathbf{x}}_i\right)$。相比之下，在参数得到充分优化之前，含参操作在迭代中传播的信息不一致。因此，无参操作通常会在开始时累积较大的权重（即 ${\alpha }_{i,j}^o$），这使得含参操作即使在经过良好训练之后也很难击败它们。当（执行结构搜索的）代理数据集很难时，这种现象尤其显著，这阻碍了 DARTS 在 ImageNet 上获得令人满意的搜索结果。

• 不利的一面是，和 DARTS 一样，在一个单元格中，每个输出节点 ${\mathbf{x}}_j$ 需要从其先例 $\left\{{\mathbf{x}}_0,{\mathbf{x}}_1,\dots ,{\mathbf{x}}_{j-1}\right\}$ 中选取两个输入节点，候选操作权重为 ${\max }_o{\alpha }_{0,j}^o,{\max }_o{\alpha }_{1,j}^o,\dots ,{\max }_o{\alpha }_{j-1,j}^o$。然而，这些架构参数通过迭代中的随机采样通道进行优化。因此，当采样通道随时间变化时，由它们确定的最佳连接性可能不稳定。这可能导致所得网络架构中出现预期之外的波动。为了缓解这个问题，PC-DARTS 引入了边正则化，${\beta }_{i,j}$ 明确地权衡每个边 $\left(i,j\right)$，因此 ${\mathbf{x}}_j$ 的计算成为：
  $${\mathbf{x}}_j^{\mathrm{P}\mathrm{C}}=\sum _{i<j}\frac{\exp \left\{{\beta }_{i,j}\right\}}{{\sum }_{i^{\prime }<j}\exp \left\{{\beta }_{i^{\prime },j}\right\}}\cdot f_{i,j}\left({\mathbf{x}}_i\right).$$

具体来说，在架构搜索完成后，边 $\left(i,j\right)$ 的连接由 $\left\{{\alpha }_{i,j}^o\right\}$ 和 ${\beta }_{i,j}$ 确定。PC-DARTS 归一化系数，然后相乘，即 $\frac{\exp \left\{{\beta }_{i,j}\right\}}{{\sum }_{i^{\prime }<j}\exp \left\{{\beta }_{i^{\prime },j}\right\}}\cdot \frac{\exp \left\{{\alpha }_{i,j}^o\right\}}{{\sum }_{o^{\prime }\in \mathcal{O}}\exp \left\{{\alpha }_{i,j}^{o^{\prime }}\right\}}$。 由于 ${\beta }_{i,j}$ 在训练过程中共享，因此学习的网络架构不易受迭代间采样通道影响，从而使架构搜索更加稳定。

P-DARTS 在 skip-connect 之后应用了 dropout，以避免参数化和无参数操作之间的信息不平衡。

SNAS

随机神经网络架构搜索（Stochastic Neural Architecture Search，SNAS），是商汤发表在 ICLR 2019上的一篇文章，吸收了 ENAS 和 DARTS 的优点。SNAS 的实质似乎就是将 DARTS 中的 Softmax 换成了Concrete distribution 并加了资源约束项，然而整个叙述却十分复杂。SNAS 在同一轮反向传播中训练神经运算的参数和架构的分布参数（这样真的好？）。号称的思想是，利用泛化损失中的梯度信息提高基于强化学习的 NAS 的效率。

• 与基于强化学习的方法[ENAS]相比，SNAS 的搜索优化可微分，搜索效率更高，可以在更少的迭代次数下收敛到更高准确率。
• 与其他可微分的方法[DARTS]相比，SNAS 直接优化 NAS 任务的目标函数，搜索结果偏差更小，可以直接通过一阶优化搜索。
• 同时优化网络损失函数的期望和网络前向时延的期望，可以自动生成硬件友好的稀疏网络。

SNAS 的实验设置基本与 DARTS 相同。

SNAS 将子网络运行延迟作为目标的正规化项：

$$\begin{array}{r}{\mathbb{E}}_{Z\sim p_{\alpha }(Z)}[L_{\theta }(Z)+\eta C(Z)]={\mathbb{E}}_{Z\sim p_{\alpha }(Z)}[L_{\theta }(Z)]+\eta {\mathbb{E}}_{Z\sim p_{\alpha }(Z)}[C(Z)],\end{array}$$
其中 $C(Z)$ 是与随机变量 $Z$ 相关联的子网络的时间成本，包含3项指标：

• 参数量;
• 浮点运算（float-point operations， FLOPs）的数量;
• 内存访问成本（memory access cost，MAC）。

FBNet

与 BSN 相同，FBNet 以随机超网络表示搜索空间。将寻找最佳架构的问题放宽为找到产生最优体系结构的分布。借助于 Gumbel Softmax 可以使用基于梯度的优化（如 SGD）直接训练架构分布。损失包括交叉熵损失和延迟损失。相当于宏搜索版的 SNAS。

随机超网络对候选块进行采样，采样概率为
$$P_{{\mathbf{\theta }}_l}(b_l=b_{l,i})=\text{softmax}({\theta }_{l,i};{\mathbf{\theta }}_l)=\frac{\exp ({\theta }_{l,i})}{{\sum }_i\exp ({\theta }_{l,i})}.$$
${\mathbf{\theta }}_l$ 包含的参数确定在第 $l$ 层采样每个块的概率。同样，第 $l$ 层的输出可以表示为
$$x_{l+1}=\sum _i{m}_{l,i}\cdot b_{l,i}(x_l),$$
其中 $m_{l,i}$ 是 $\{0,1\}$ 中的随机变量，如果采样块 $b_{l,i}$，则计算结果为1。采样概率由前面的等式确定。$b_{l,i}(x_l)$ 表示给定输入特征图 $x_l$ 的情况下，第 $l$ 层的第 $i$ 块的输出。FBNet 让每个层独立采样，因此，采样架构 $a$ 的概率可以描述为
$$P_{\mathbf{\theta }}(a)=\prod _l{P}_{{\mathbf{\theta }}_l}(b_l=b_{l,i}^{(a)}),$$
其中 $\mathbf{\theta }$ 为一个向量，元素 ${\theta }_{l,i}$ 为第 $i$ 块的第 $l$ 层的采样参数。 $b_{l,i}^{(a)}$ 表示在采样架构中 $a$，在第 $l$ 层中选中第 $i$ 个块。

松弛求解最佳架构 $a\in \mathcal{A}$ 问题为优化随机超网络的概率 $P_{\theta }$ 以实现最小预期损失，公式重写为
$$\underset{\mathbf{\theta }}{\min }\underset{w_a}{\min }{\mathbf{E}}_{a\sim P_{\mathbf{\theta }}}\{\mathcal{L}(a,w_a)\}.$$

将离散掩码变量 $m_{l,i}$ 放宽为由 Gumbel Softmax 函数计算的连续随机变量：
$$\begin{array}{rl}{m}_{l,i}& =\text{GumbelSoftmax}({\theta }_{l,i}|{\mathbf{\theta }}_{\mathbf{l}})\\ & =\frac{\exp [({\theta }_{l,i}+g_{l,i})/\tau ]}{{\sum }_i\exp [({\theta }_{l,i}+g_{l,i})/\tau ]},\end{array}$$
其中 $g_{l,i}\sim \text{Gumbel(0, 1)}$ 是 Gumbel 分布的随机噪声。Gumbel Softmax 函数由温度参数 $\tau$ 控制。当 $\tau$ 接近0时，它近似于 $P_{\mathbf{\theta }}(a)={\prod }_l{P}_{{\mathbf{\theta }}_l}(b_l=b_{l,i}^{(a)})$ 中分布的离散分类抽样。随着 $\tau$ 变大，$m_{l,i}$ 成为一个连续的随机变量。无论 $\tau$ 的值如何，掩码 $m_{l,i}$ 都对参数 ${\theta }_{l,i}$ 可微。DNAS 和 SNAS 同样使用 Gumbel Softmax 进行网络结构搜索。

对于延迟项，FBNet 使用基于查找表的模型进行效率估计，因此 $\text{LAT}(a)$ 公式可以写为
$$\text{LAT}(a)=\sum _l\sum _i{m}_{l,i}\cdot \text{LAT}(b_{l,i}).$$
每个运算符 $\text{LAT}(b_{l,i})$ 的延迟是一个常数系数，从而架构 $a$ 的整体延迟相对于掩码 $m_{l,i}$ 是可微分的。

训练过程为：

• 随机取 ImageNet 的100类在8 GPU 机器上训练随机超网络90个 epoch，batchsize=192；
• 挑选出最优结构后，在 ImageNet 上训练360个 epoch，batchsize=256。

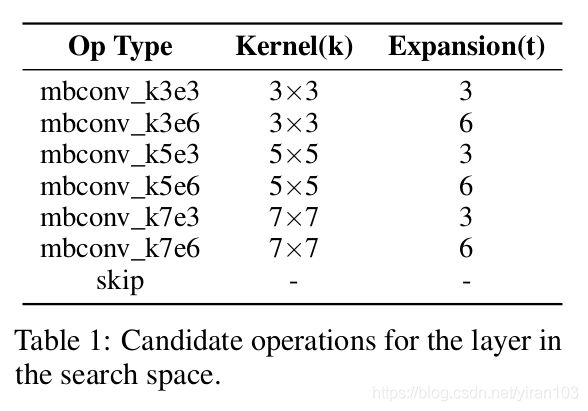
FBNet 的搜索空间参考 MobileNetV2 和 ShiftNet ，网络首尾固定，中间的22层可调，如 Table 1 所示。

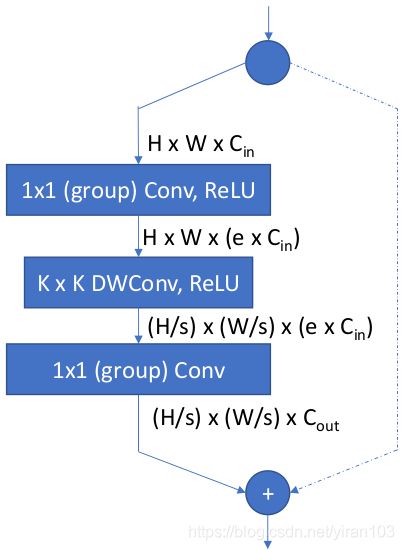
块结构如下图所示，深度分离卷积可选3x3或5x5的卷积核，块内的首尾1x1卷积可替换为 group + channel shuffle。

值得注意的是网络没有使用 BN，论文也未谈到这一点。但 fbnet_builder 中是有的。

从 ImageNet 中随即取100类作为训练集，历经90个 epoch。找到最优结构后，从头训练模型。损失函数为：
$$\begin{array}{r}\mathcal{L}(a,w_a)=\text{ CE}(a,w_a)\cdot \alpha \log (\text{LAT}(a){)}^{\beta }\end{array}$$
第一项 $\text{CE}(a,w_a)$ 表示架构 $a$ 与相应参数 $w_a$ 的交叉熵损失。第二项 $\text{LAT}(a)$ 表示目标硬件上体系结构的延迟，以微秒为单位。系数 $\alpha$ 控制损失函数的总体大小。指数系数 $\beta$ 调制延迟项的大小。除了 log 外，形式与 MnasNet 类似。

FBNet 预先测试每个 op 的耗时，创建查找表来估计不同模型的延时。目标设备为 Samsung Galaxy S8和 iPhone X。

$$\begin{array}{r}\text{LAT}(a)=\sum _l\text{LAT}(b_l^{(a)}),\end{array}$$

其中 $b_l^{(a)}$ 表示架构 $a$ 来自第 $l$ 层的块。

FBNet 将模型量化到 int8 在 Caffe2上测试，为对比将其他方法也进行了转换。

ProxylessNAS

D

R

DARTS

ProxylessNAS

BinaryConnect

REINFORCE

MobileNetV2

可微 NAS 通过网络架构的连续表示来降低训练时长，但会遇到高 GPU 内存消耗问题（随候选集大小线性增长）。ProxylessNAS 着眼于减少内存消耗，在训练时采样两条路径。采用强化学习和梯度下降两种方法训练 CPU、GPU 以及移动处理器3个平台上的模型。文中试图套用 BinaryConnect ，大讲二值化。然而路径二值化并不能降低内存消耗，实际运行机理与此毫不相干。直接在目标数据集上训练也有点噱头，因为分摊下来每条路径的训练轮数不多。论文题目不如改成随机采样更新的 Softmax 近似。而且，采样路径却未提 BatchNorm 如何应对。一个鲜明的例子是 DenseNAS 也使用路径采样方法，但未提及二值化。

ProxylessNAS 受 DARTS 和 One-Shot 的启发 ， 将 NAS 定义为路径级修剪过程。

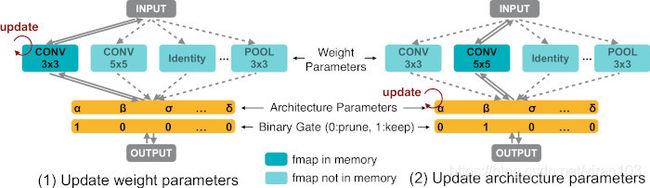
ProxylessNAS 在目标硬件上学习专用网络结构，但硬件目标（以延迟为例）不可微分。为此，其将网络延迟建模为连续函数，并作为正则化损失进行优化，类似于 SNAS。此外，ProxylessNAS 还提出了一种基于 REINFORCE规则 的算法（Proxyless-R），作为处理硬件度量的替代策略。

ProxylessNAS 将路径 N 选择一分解为多个二进制选择任务。 直觉是，如果一条路径是特定位置的最佳选择，那么与任何其他路径相比，它应该是更好的选择。

在结构参数的更新步骤中：

• 首先根据多项分布 $(p_1,\cdots ,p_N)$ 对两条路径进行采样，并屏蔽所有其他路径，就好像它们不存在一样。因此，候选数暂时从 $N$ 减少到2，而路径权重 $\{p_i\}$ 和二进制门 $\{g_i\}$ 相应地重置。
• 然后，我们使用通过公式(4)计算的梯度更新这两个采样路径的架构参数。
• 最后，由于通过将 softmax 应用于架构参数来计算路径权重，需要通过乘以比率来重新调整这两个更新的架构参数的值，以保持未采样路径的路径权重不变。

这样，在每个更新步骤中，一个采样路径被增强（路径权重增大），另一个采样路径被衰减（路径权重减小），而所有其他路径保持不变。这样，无论 $N$ 的值如何，在架构参数的每个更新步骤中仅涉及两条路径，从而将内存需求降低到训练紧凑模型的相同水平。

为了使延迟可微分，ProxylessNAS 将网络的延迟建模为神经网络维度的连续函数。考虑具有候选集 $\{o_j\}$ 的混合操作，并且每个 $o_j$ 与路径权重 $p_j$ 相关联，该权重表示选择 $o_j$ 的概率。因此，混合操作（即可学习块）的预期延迟如下：
$$\mathbb{E}[{\text{latency}}_i]=\sum _j{p}_j^i\times F(o_j^i),$$
其中 $\mathbb{E}[{\text{latency}}_i]$ 是 $i^{th}$ 可学习块的预期延迟，$F(\cdot )$ 表示延迟预测模型，$F(o_j^i)$ 是 $o_j^i$ 的预测延迟。因此，$\mathbb{E}[{\text{latency}}_i]$ 关于体系结构参数的梯度为： $\partial \mathbb{E}[{\text{latency}}_i]/\partial p_j^i=F(o_j^i)$。

对于具有一系列混合操作的整个网络，由于这些操作在推理期间按顺序执行，因此网络的预期延迟可以用这些混合操作的总预期延迟之和表示：
$$\mathbb{E}[\text{latency}]=\sum _i\mathbb{E}[{\text{latency}}_i],$$

Proxyless-G 通过乘以比例因子 ${\lambda }_2(>0)$ 将网络的预期延迟纳入正常损失函数，该比例因子控制精度和延迟之间的权衡。最终的损失函数给出为

$$Loss=Los{s}_{CE}+{\lambda }_1||w|{|}_2^2+{\lambda }_2\mathbb{E}[\text{latency}],$$
其中 $Los{s}_{CE}$ 表示交叉熵损失，${\lambda }_1||w|{|}_2^2$ 是权重衰减项。

ProxylessNAS 还可以利用 REINFORCE 来训练二值化权重。考虑具有二进制化参数 $\alpha$ 的网络，更新二进制化参数的目的是找到最大化某个奖励 $R(\cdot )$ 的最佳二进制门 $g$ 。为便于说明，这里假设网络只有一个混合操作。因此，根据 REINFORCE ，对二进制化参数进行了以下更新：
$$\begin{array}{rl}J(\alpha )& ={\mathbb{E}}_{g\sim \alpha }[R({\mathcal{N}}_g)]=\sum _i{p}_{i}R(\mathcal{N}(e=o_i)),\\ {\nabla }_{\alpha }J(\alpha )& =\sum _{i}R(\mathcal{N}(e=o_i)){\nabla }_{\alpha }{p}_i=\sum _{i}R(\mathcal{N}(e=o_i))p_i{\nabla }_{\alpha }\log (p_i),\\ & ={\mathbb{E}}_{g\sim \alpha }[R({\mathcal{N}}_g){\nabla }_{\alpha }\log (p(g))]\approx \frac{1}{M}\sum _{i=1}^{M}R({\mathcal{N}}_{g^i}){\nabla }_{\alpha }\log (p(g^i)),\end{array}$$

其中 $g^i$ 表示第 $i^{th}$ 个采样二进制门，$p(g^i)$ 表示根据公式2采样 $g^i$ 的概率，${\mathcal{N}}_{g^i}$ 是根据二进制门 $g^i$ 的紧凑型网络。由于上式不需要 $R({\mathcal{N}}_g)$ 对 $g$ 可微，因此它可以处理不可微分的目标。一个有趣的观察是，公式eq:reinforce具有与标准 NAS 类似的形式，但它不是一个连续的决策过程，并且没有使用 RNN 元控制器。此外，由于基于梯度的更新和基于 REINFORCE 的更新对于相同的二值化体系结构参数基本上是两个不同的更新规则，因此可以将它们组合以形成体系结构参数的新更新规则。

Proxyless-R 与 MnasNet 类似，使用 $ACC(m)\times [LAT(m)/T{]}^w$ 作为优化目标，其中 $ACC(m)$ 表示模型 $m$ 的准确率，$LAT(m)$ 表示 $m$ 的延迟，$T$ 是目标延迟，$w$ 是用于控制准确性和延迟之间权衡的超参数。

ProxylessNAS 与 DARTS 在验证集上训练结构参数 $\alpha$，而 FBNet 未进行划分。

ProxylessNAS 设置一系列 MBConv，卷积核大小可选 $\{3,5,7\}$ 扩张系数为 $\{3,6\}$。

令人困惑的是 ProxylessNAS 的 batchsize=256，FBNet 为192。FBNet 只用 ImageNet 的1/10，ProxylessNAS 使用全部，二者训练时间却相同。FBNet 估计 MnasNet 的成本为91000 GPU hours；ProxylessNAS 实现的是40000。假定 ProxylessNAS 用的是 V100（测试平台是这一型号）， FBNet 的设备似乎与之存在代差。

Single-Path NAS

Single-Path NAS 是一种单路径（或者 superkernel）方法。用一个7x7的大卷积，来代表3x3、5x5和7x7的三种卷积，把外边一圈 mask 清零掉就变成了3x3或5x5。扩张系数类似，认为6包含两个3，实现高度的参数复用。

省显存，然而本质还是搜索空间小。基础网络参考 FBNet，仅搜索 expansion rate 和 kernel size。Single-Path NAS 代码 dstamoulis/single-path-nas 完全开源，依赖 TensorFlow 和 TPU，使用 facebook/FAI-PEP 分析模型每层的运行时间。比较有意思的是文中的表格，几种搜索算法结果并未拉开差距。

DenseNAS

DenseNAS 由地平线和华中科技大学联合提出，号称可以搜索网络结构中每个 block 的宽度和对应的空间分辨率。DenseNAS 构建一个密集连接的搜索空间。每个块的滤波器的数量（即宽度）以小步幅逐渐增加。搜索空间参考 MobileNetV2 并采用密集连接的形式构建。搜索空间比之前一些算法大。然而 DenseNAS 与 FBNet 一样训练集取 ImageNet 的1/10，同时类似 ProxylessNAS 采样路径训练，反而比二者训练时间缩短一半。

如下图所示，DenseNAS 在三个不同的级别（layer、block 和 network）定义搜索空间：

• 每个层都包含所有候选操作；
• 一个块可以分为两个组件：头部层和堆叠层；
• 整个网络使用具有增量宽度的块构建。
  

层为搜索空间中的基本结构。一层代表一组候选操作。搜索空间中的操作集合如表 Table 1 所示。

每个块由若干层组成，拥有固定宽度和相应的空间分辨率。头部层处理具有不同通道数和空间分辨率的输入张量，并转换为固定宽度和空间分辨率。头部层不包括跳过连接，因为它是所有块所必需的。头部层之后是许多堆叠层（图中的例子中是三层）。之后，堆叠层中的操作以相同数量的通道和空间分辨率执行。

MnasNet、ProxylessNAS 和 FBNet 设置固定数量的块。DenseNAS 在搜索空间中设计了更多具有不同宽度的块，并允许搜索架构只包含块的子集，从而使搜索算法能够自由地选择具有特定宽度的块，同时丢弃其他块。

整个超网络架构定义为 $Arch$，并假设它包含 $N$ 个块：$Arch=\{B_1,B_2,...,B_N\}$。 DenseNAS 将整个网络划分为几个阶段。每个阶段拥有不同的宽度范围和固定的空间分辨率。超网络从头到尾，块的宽度以小步幅逐渐增长。网络的早期阶段设定较小的宽度增长步幅，因为设置较大将导致巨大的计算成本。后期阶段增长幅度逐渐变大。如结构图所示，在第3阶段，空间分辨率设置为 $28\times 28$，宽度增长步幅为8。宽度增长步幅在第4阶段变为16，阶段5变为64。

定义块 $B_i$ 和后续块 $B_j$（$j>i$）之间的连接为 $C_{ij}$。$B_i$ 和 $B_j$ 的空间分辨率分别为 $H_i\times W_i$（通常 $H_i=W_i$）和 $H_j\times W_j$。DenseNAS 限制连接仅在空间分辨率相差不超过两倍的块之间。因此，当 $j-i\le m$ 且 $H_j/H_i\le 2$ 时，$C_{ij}$ 存在。搜索空间基于密集连接的块构建。 但是，只选择一条路径来导出最终的结构。DenseNAS 不仅搜索每个块中的层数，而且还搜索块宽度和块数。同时确定执行空间下采样的层。目标是在搜索空间中找到一条良好的路径，代表架构的最佳深度和宽度配置。

设 $b_i$ 为第 $i$ 个块 $B_i$ 的输出张量。每个块连接到后续 $m$ 块。为了将块连接松弛为连续表示，DenseNAS 为块的每个输出路径分配块级架构参数。也就是说，对于从块 $B_i$ 到 $B_j$ 的路径，它们之间的路径有一个参数 ${\beta }_{ij}$。与计算每个操作的权重类似，使用 softmax 函数计算两个块之间所有路径的概率：
$$p_{ij}=\frac{\exp ({\beta }_{ij})}{{\sum }_{k=1}^m\exp ({\beta }_{ik})}.$$

假设块 $B_i$ 需要来自先前块的 $m^{\prime }$ 输入张量，即 $B_{i-m^{\prime }}$, $B_{i-m^{\prime }+1}$, $B_{i-m^{\prime }+2}$ … $B_{i-1}$。来自这些块的输入张量在通道数和空间分辨率上有所不同。因此，每个输入张量由 $B_i$ 中的头部层变换为统一大小，然后求和。设 $H_{ik}$ 表示块 $B_i$ 中第 $k$ 个头部层对输入张量 $B_{i-k}$ 的转换，其中 $k=1..m^{\prime }$。转换后的输入张量之和可通过以下公式计算：

$$x_i=\sum _{k=1}^{m^{\prime }}{p}_{i-k,i}\cdot H_{ik}(x_{i-k}).$$

值得注意的是，路径概率在块输出维度上标准化，但应用于后续块的输入维度（更具体地说，在头部层上）。头部层本质上是是候选操作的混合加权和。层级参数 $\alpha$ 控制要选择的操作，而外部块级参数 $\beta$ 决定要连接的块。
DenseNAS 的训练方式与 DARTS 类似，权重和架构的优化过程按 epoch 交替进行。搜索过程完成后，根据结构参数导出体系结构：

• 在层级别，选择具有最大体系结构权重的候选操作，即 $argma{x}_{o\in \mathcal{O}}{\alpha }_o^{\ell }$；
• 在网络级，使用 Viterbi 算法根据每个块的输出路径概率来选择连接具有最高总转移概率的块的路径。

超网络包括搜索空间中的所有可能路径和操作。 one-shot 搜索方法在训练超级网络时会丢掉一些路径。该技术使独立模型的性能预测更准确。为了减少内存消耗并加快搜索过程，DenseNAS 采用了 drop-path 训练策略：

• 当训练操作权重时，DenseNAS 在每一层根据结构参数分布 $\{{\alpha }_o^{\ell }|o\in \mathcal{O}\}$ 从候选操作中采样出一条路径。丢弃路径训练不仅加速了搜索，而且减弱了搜索空间中不同结构的操作权重之间的耦合效应。
• 训练结构参数时，像 ProxylessNAS一样根据结构权重分布在每个层中对两个操作进行采样。为了保持未采样的操作的体系结构权重不变，DenseNAS 计算重新平衡偏差以调整采样和新更新的参数。
  $${\mathtt{b}\mathtt{i}\mathtt{a}\mathtt{s}}_s=\ln \frac{{\sum }_{o\in {\mathcal{O}}_s}\exp ({\alpha }_o^{\ell })}{{\sum }_{o\in {\mathcal{O}}_s}\exp ({{\alpha }^{\prime }}_o^{\ell })}$$
  其中 ${\mathcal{O}}_s$ 指的是采样的一组操作，${\alpha }_o^{\ell }$ 指的是层 $\ell$ 中最初采样的结构参数，${{\alpha }^{\prime }}_o^{\ell }$ 是相应更新后的结构参数。训练时 ${\mathtt{b}\mathtt{i}\mathtt{a}\mathtt{s}}_s$ 不断累加？

DSO-NAS

DSO-NAS 是初创企业图森未来的一篇文章，投 ICLR 2019 被拒。文中对比了不同方法的参数量和计算量。评审中附加了更多实验数据，从中可以看出在网络延迟方面不尽人意。
DSO-NAS 与 ProxylessNAS 一样将网络搜索看作是剪枝过程，采用团队前作 SSS(Sparse Structure Selection) 进行优化。不同的是 DSO-NAS 的 block 内部细分为4层，连接较为复杂。

参考资料：

• 如何评价google Searching for MobileNetV3？
• The Lightweight Face Recognition Challenge
• guan-yuan/awesome-AutoML-and-Lightweight-Models
• Literature on Neural Architecture Search
• D-X-Y/Awesome-NAS
• google-research/nasbench
• microsoft/nni
• 神经网络架构搜索（Neural Architecture Search）杂谈
• Xuanyi Dong
• ENAS的原理和代码解析
• 业界 | 谷歌提出移动端AutoML模型MnasNet：精度无损速度更快
• 多图演示高效的神经架构搜索
• Gumbel-Softmax Trick和Gumbel分布
• 旷视提出One-Shot模型搜索框架的新变体
• 另一种可微架构搜索：商汤提出在反传中学习架构参数的SNAS
• ICLR 2019｜随机神经网络结构搜索 (SNAS)
• 论文笔记系列-Neural Architecture Search With Reinforcement Learning
• ENAS: 更有效地设计神经网络模型(AutoML)
• 万字解读商汤科技ICLR2019论文：随机神经网络结构搜索
• 同济和华为诺亚提出：渐进式可微网络结构搜索，显著提升可微式搜索的性能和稳定性，已开源
• 论文解读：Single-Path NAS
• 【ICLR 19】DARTS可微网络结构搜索
• CVPR 2018 | 商汤科技Oral论文详解：BlockQNN自动网络设计方法
• AutoML：NAS 之 Randomly Wired Neural Networks
• A Survey on Neural Architecture Search
• Neural architecture search
• AutoML (1) - Introduction
• Review: NASNet — Neural Architecture Search Network (Image Classification)
• ENAS的原理和代码解析
• 论文笔记系列-Neural Architecture Search With Reinforcement Learning
• 旷视首席科学家孙剑：深度学习变革视觉计算丨CCF-GAIR 2019
• DenseNAS：密集连接搜索空间下的高灵活度网络结构搜索 | 大牛讲堂
• 强化学习系列（六）：时间差分算法（Temporal-Difference Learning)
• 强化学习 - 时间差分学习(Temporal-Difference Learning)
• A3C、PPO、GAE笔记
• One-Shot 神经网络搜索(NAS)的searching阶段到底在做什么？
• AutoML for Object Detection
• 解读小米MoGA：超过MobileNetV3的移动端GPU敏感型搜索
• 如何通俗地讲解 viterbi 算法？