Reverse Influence Sampling in Python(译文)
影响最大化(IM)问题寻求网络中的一组种子节点,以最大化通过在该种子集启动的影响级联激活的预期节点数。先前的文章比较了两种IM算法Kempe等人(2003) 的Greedy算法和 Leskovec等人 的CELF算法(2007)。多年来,CELF(以及Goyal等人于2011年修改的CELF ++版本)是最快的IM算法,具有理论上可保证的性能范围。随后的文献主要侧重于通过启发式来提高计算效率,而启发式则牺牲了对速度的理论保证。然而,最近,出现了一种新的解决方法-反向影响采样(RIS),该方法既快速又在理论上得到了保证,现在已成为最先进的IM方法之一。这篇文章逐步介绍了RIS算法在Python中的实现,并将其解决方案和计算速度与上一篇文章中描述的CELF算法进行了比较。
The Reverse Influence Sampling Algorithm
启用RIS系列算法的关键见解是Borgs 等人将随机反向可达集的概念引入IM问题(2014)。通过首先从原图中根据边缘的传播概率 1 − p e 1-p_e 1−pe 去掉其中某些边 e e e, 得到采样图 g g g,然后取 g g g 中可以“到达”的节点集来生成针对任意节点 v v v 的反向可达集 (RR)。随机反向可达集 (RRR) 只是针对随机选择的均匀节点的RR集。下面是一个可视示例。根据每个边缘分配的概率从左边的原始网络 G G G 采样边缘(本文中的代码假定所有边缘共享相同的传播概率,因此 p e = p p_e = p pe=p)。这将在中间图形中生成一个采样网络 g g g,在该网络中倾向于选择具有较高概率的边缘。选择一个随机节点D,然后得到的RRR集由具有指向D的定向路径的那些节点组成,这些节点被虚线包围。
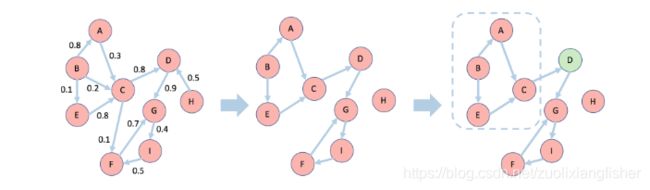
直观地,如果一个节点 u u u 出现在另一个节点 v v v 的RR集中,则存在从 u u u 到 v v v 的定向路径。因此,包含 u u u 的种子集的扩散过程具有激活 v v v 的可能性。节点激活以引理形式化,该引理指出,来自任何种子集 S S S 的扩散过程将激活任何节点 v v v 的概率等于针对 v v v 的RR集内包含 S S S 中至少一个节点的概率 (参考 Borgs et al 2014)。基于此引理,RIS算法系列分两个步骤进行:
- 生成许多独立的RRR集的集合 R R R。
- 使用标准贪婪算法选择 k k k 个节点以覆盖 R R R 中的最大RRR集数量,该算法可获得该问题的 ( 1 − 1 / e − ϵ ) (1-1/e-\epsilon) (1−1/e−ϵ) 近似解。
该方法之所以有效,是因为对于任何种子集 S S S,由 S S S 覆盖的 R R R 中的RRR集的比例都是 S S S 传播的无偏估计(由于上述引理)。因此, R R R 中覆盖大量RR集的种子集可能具有较大的预期影响,这使其成为IM问题的良好解决方案。
RIS算法具有很高的计算性能的关键在于,与Greedy或CELF不同,它不会重复使用扩展计算过程来逐步构建该问题的解。取而代之的是,它先执行所有的蒙特卡洛模拟/采样以构造 R R R,然后从中选择整个种子集。因此,该方法避免了贪婪算法及其大多数后继算法的“浪费”扩展计算,因为生成的RRR集用于通知网络内所有节点的扩展。
下面,我用两个单独的函数描述RIS算法的实现。第一个是 get_RRS(),它具有图和传播概率,并散出随机的反向可达集。第二个 ris()使用第一个函数生成大量随机反向可到达集,然后将其用于选择有影响力的种子集。我们首先加载一些软件包:
%matplotlib inline
import matplotlib.pyplot as plt
from random import uniform, seed
import numpy as np
import pandas as pd
import time
from igraph import *
import random
from collections import Counter
Create Random Reverse Reachable Set
下面的get_RRS() 函数获取一个网络对象,并从该网络生成一个RRR集。网络在dataframe(numpy中的一个数据结构,类似矩阵) G 中定义,其中每一行代表网络中的有向边,两列['source','target'] 分别描述给定边的源节点和目标节点。有很多方法可以用Python表示网络 (请参阅使用流行的 igraph 程序包实现CELF算法的博文,以及比较四种不同网络实现的博文),但是此设置是透明的,不需要了解一组方法特定于给定的图形建模包。该功能包括三个步骤:
- 从
G的源列中包含的所有潜在源节点的集合中随机选择源节点。 - 通过将传播参数 p p p 与均匀随机抽签进行比较以模拟每个边的采样过程,从网络
G采样实例g,然后将抽取的那些边保存在新的dataframe中,代表采样图。这与下面的IC()函数中用于模拟传播的方法非常相似,这暗示了RIS为什么起作用。 - 通过迭代过程自己生成RR集,该过程首先找到边上通向
source的所有节点,然后将其添加到RRS列表对象。然后,循环将找到所有边都通向上一步中找到的新节点的节点,依此类推。网络的dataframe表示使此过程非常容易,因为我们仅基于目标列进行过滤,然后从源列中选择“新节点”。替代表示将需要某种形式的邻近功能。
def get_RRS(G,p):
"""
Inputs: G: Ex2 dataframe of directed edges. Columns: ['source','target']
p: Disease propagation probability
Return: A random reverse reachable set expressed as a list of nodes
"""
# Step 1. Select random source node
source = random.choice(np.unique(G['source']))
# Step 2. Get an instance of g from G by sampling edges
g = G.copy().loc[np.random.uniform(0,1,G.shape[0]) < p]
# Step 3. Construct reverse reachable set of the random source node
new_nodes, RRS0 = [source], [source]
while new_nodes:
# Limit to edges that flow into the source node
temp = g.loc[g['target'].isin(new_nodes)]
# Extract the nodes flowing into the source node
temp = temp['source'].tolist()
# Add new set of in-neighbors to the RRS
RRS = list(set(RRS0 + temp))
# Find what new nodes were added
new_nodes = list(set(RRS) - set(RRS0))
# Reset loop variables
RRS0 = RRS[:]
return(RRS)
Create RIS algorithm
ris() 函数分两步实现了实际的RIS解决方案过程:
- 通过遍历
get_RRS()函数,生成包含mc个种子的随机反向可达集的大集合 R R R。 - 运行“最大贪婪覆盖率”算法,该算法仅查找 RRR 集中出现最多的节点。 一旦找到此节点,将从集合 R R R 中删除具有该节点特征的 RRR 集,然后重复该过程,直到选择了 k k k 个节点并将其存储在列表对象
SEED中为止。
在此过程中,我们还跟踪时间,将其与下面的CELF运行时间进行比较。
def ris(G,k,p=0.5,mc=1000):
"""
Inputs: G: Ex2 dataframe of directed edges. Columns: ['source','target']
k: Size of seed set
p: Disease propagation probability
mc: Number of RRSs to generate
Return: A seed set of nodes as an approximate solution to the IM problem
"""
# Step 1. Generate the collection of random RRSs
start_time = time.time()
R = [get_RRS(G,p) for _ in range(mc)]
# Step 2. Choose nodes that appear most often (maximum coverage greedy algorithm)
SEED, timelapse = [], []
for _ in range(k):
# Find node that occurs most often in R and add to seed set
flat_list = [item for sublist in R for item in sublist]
seed = Counter(flat_list).most_common()[0][0]
SEED.append(seed)
# Remove RRSs containing last chosen seed
R = [rrs for rrs in R if seed not in rrs]
# Record Time
timelapse.append(time.time() - start_time)
return(sorted(SEED),timelapse)
Recap: Independent Cascade and CELF
下面是独立的级联传播函数 IC(),用于计算网络中给定种子集的传播;而 celf() 函数,用于输入一个网络然后使用CELF算法查找最有影响力的节点。 有关这些功能的更详细说明,请参见上一篇文章。 但是请注意,这些函数稍有不同,因为它们在上述函数中使用了相同的网络 dataframe 表示形式(而不是先前文章中的igraph表示形式)。
def IC(G,S,p=0.5,mc=1000):
"""
Input: G: Ex2 dataframe of directed edges. Columns: ['source','target']
S: Set of seed nodes
p: Disease propagation probability
mc: Number of Monte-Carlo simulations
Output: Average number of nodes influenced by the seed nodes
"""
# Loop over the Monte-Carlo Simulations
spread = []
for _ in range(mc):
# Simulate propagation process
new_active, A = S[:], S[:]
while new_active:
# Get edges that flow out of each newly active node
temp = G.loc[G['source'].isin(new_active)]
# Extract the out-neighbors of those nodes
targets = temp['target'].tolist()
# Determine those neighbors that become infected
success = np.random.uniform(0,1,len(targets)) < p
new_ones = np.extract(success, targets)
# Create a list of nodes that weren't previously activated
new_active = list(set(new_ones) - set(A))
# Add newly activated nodes to the set of activated nodes
A += new_active
spread.append(len(A))
return(np.mean(spread))
def celf(G,k,p=0.5,mc=1000):
"""
Inputs: G: Ex2 dataframe of directed edges. Columns: ['source','target']
k: Size of seed set
p: Disease propagation probability
mc: Number of Monte-Carlo simulations
Return: A seed set of nodes as an approximate solution to the IM problem
"""
# --------------------
# Find the first node with greedy algorithm
# --------------------
# Compute marginal gain for each node
candidates, start_time = np.unique(G['source']), time.time()
marg_gain = [IC(G,[node],p=p,mc=mc) for node in candidates]
# Create the sorted list of nodes and their marginal gain
Q = sorted(zip(candidates,marg_gain), key = lambda x: x[1],reverse=True)
# Select the first node and remove from candidate list
S, spread, Q = [Q[0][0]], Q[0][1], Q[1:]
timelapse = [time.time() - start_time]
# --------------------
# Find the next k-1 nodes using the CELF list-sorting procedure
# --------------------
for _ in range(k-1):
check = False
while not check:
# Recalculate spread of top node
current = Q[0][0]
# Evaluate the spread function and store the marginal gain in the list
Q[0] = (current,IC(G,S+[current],p=p,mc=mc) - spread)
# Re-sort the list
Q = sorted(Q, key = lambda x: x[1], reverse=True)
# Check if previous top node stayed on top after the sort
check = Q[0][0] == current
# Select the next node
S.append(Q[0][0])
spread = Q[0][1]
timelapse.append(time.time() - start_time)
# Remove the selected node from the list
Q = Q[1:]
return(sorted(S),timelapse)
简单总结一下IC模型,IC模型已知图网络 G 和 种子集合 S,首先初始化新激活的和已经激活的用户均为种子集 S,然后直到没有新种子被激活前,每次循环首先找出种子集合影响的目标用户集,根据激活概率判断目标用户中哪些被激活,然后将本轮激活的用户除去已经在此前激活过的部分,将增量部分加入到已激活的用户 A A A 里,计算本轮已激活用户集 A A A 的大小,作为本轮传播影响力,迭代直到没有新节点被激活。
CELF模型用于选取影响力最大的 k k k 个节点,首先已知图网络 G 和激活概率 p ,第一轮从便利图中全量节点,利用IC模型输出每个节点的影响力,选择影响力最大的一个,然后再循环选择剩下的 k k k-1个,每次更新选择增量影响力增加最大的节点,直到选出全部节点。
Example 1: A Simple Test Run
我们将首先测试RIS算法,看看它能否为我们知道两个最有影响力的节点的简单玩具示例识别正确的解决方案。 下面我们创建一个10节点/ 20边缘定向网络,其中节点0和1最有影响力。 为此,我们创建了8个从0和1传出的链接,而其他8个节点最多只有一个。 我们还确保0和1不是邻居,以便在种子集中拥有一个不会使另一个成为多余。 通过绘制网络,我们可以直观地了解节点0和1最具影响力的原因。
# Create simple network with 0 and 1 as the influential nodes
source = [0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,2,3,4,5]
target = [2,3,4,5,6,7,8,9,2,3,4,5,6,7,8,9,6,7,8,9]
# Create dataframe representation
d = pd.DataFrame({
'source':source,'target':target})
# Create igraph representation for plotting
gr = Graph(directed=True)
gr.add_vertices(range(10))
gr.add_edges(zip(source,target))
# Plot graph
gr.vs["label"], gr.es["color"], gr.vs["color"] = range(10), "#B3CDE3", "#FBB4AE"
plot(gr,bbox = (200, 200), margin = 20,layout = gr.layout("kk"))
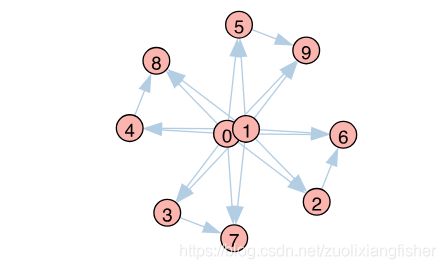
在此图上运行每种算法以找到最有影响力的k = 2大小的种子集,即可成功获得两个节点(p和mc的选择在这里并不重要)
# Run algorithms
ris_output = ris(d,2,p=0.5,mc=1000)
celf_output = celf(d,2,p=0.5,mc=1000)
# Print resulting seed set
print("RIS seed set: %s" %ris_output[0])
print("CELF seed set: %s" %celf_output[0])
RIS seed set: [0, 1]
CELF seed set: [0, 1]
Example 2: A Larger Network
现在,我们不再使用小样示例,而是考虑使用更大的100节点网络。 我们将使用 igraph 软件包中的 Barabasi 方法而不是像上面那样直接指定网络,而是自动构建通过Albert-Barabasi优先附着方法(近似于无标度网络)创建的网络。 图形类型的选择是任意的,因为任何图形的要点都不重要。 通过遍历每个边并提取源节点和目标节点,将网络转换为 dataframe 表示形式。 绘制网络图表明,我们现在正在处理一个更大,更复杂的图,其中有影响力的节点不明显。
# Generate Graph
G = Graph.Barabasi(n=100, m=3,directed=True)
# Transform into dataframe of edges
source_nodes = [edge.source for edge in G.es]
target_nodes = [edge.target for edge in G.es]
df = pd.DataFrame({
'source': source_nodes,'target': target_nodes})
# Plot graph
G.es["color"], G.vs["color"] = "#B3CDE3", "#FBB4AE"
plot(G,bbox = (280, 280),margin = 11,layout=G.layout("kk"))
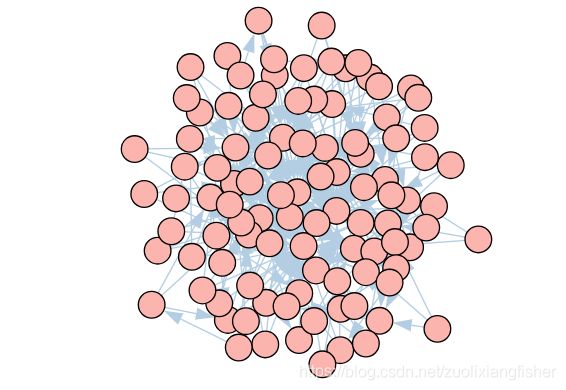
与上一篇文章中Greedy算法和CELF算法的比较不同,与上述玩具示例的结果不同,对于有限数量的Monte Carlo模拟/ RRS集,CELF和RIS方法不能产生相同的结果,这在理论上没有保证。唯一的保证是,这两种算法都产生一个种子集,该种子集以给定的概率 1 − 1 / e − ϵ 1-1/e-\epsilon 1−1/e−ϵ 接近最佳的传播影响力,但是这些集可能有所不同。
值得花时间在这里讨论每种方法中 mc 参数之间的差异,以及它们在近似中与误差项 ϵ \epsilon ϵ 的关系。在CELF中,mc 指定运行多少个不同的传播级联来计算所考虑的每个节点的平均扩展。在RIS中,mc 反而代表的是了集合R中RRS的集合的数量。因此,为每种方法设置相同的 mc 值通常将无法达到相同的准确度 ϵ \epsilon ϵ。
因此,为了进行公平的比较,我们理想地希望在每种方法中设置 mc 的各自值,以使它们都达到相同的 ϵ \epsilon ϵ。但是,这说起来容易做起来难。实际上,直到最近,文献也只是遵循Kempe等人(2003年)的观点,设置mc = 10000但没有真正理解CELF或Greedy算法中 mc 和 ϵ \epsilon ϵ 之间的关系。直到 Tang et al2014年),我们终于得到了关系的明确陈述,其表达如下。CELF至少以概率为 1 − 1 n 1-\frac{1}{n} 1−n1返回 ϵ \epsilon ϵ 的近似误差,如果将mc设置为大于 ( 8 k 2 + 2 k ϵ ) ⋅ n ⋅ ( l + 1 ) log n + log k ϵ 2 O P T (8k^{2}+2k\epsilon)\cdot n\cdot\frac{(l+1)\log n+\log k}{\epsilon^{2}OPT} (8k2+2kϵ)⋅n⋅ϵ2OPT(l+1)logn+logk
其中OPT是最大的可达影响力,在RIS算法中的等价的表达式为 ( 8 + 2 ϵ ) ⋅ n ⋅ l log n + log ( n k ) + log 2 ϵ 2 O P T (8+2\epsilon)\cdot n\cdot\frac{l\log n+\log \tbinom{n}{k}+\log 2}{\epsilon^{2}OPT} (8+2ϵ)⋅n⋅ϵ2OPTllogn+log(kn)+log2
现在,使用这些表达式的麻烦在于OPT通常是未知的 (因为我们需要知道要解决的内容才能进行计算!)。因此,在实践中,文献试图为OPT设定一个下限,这反过来又暗示了上面表达式的上限,因此对为达到给定what设置mc所做的保守估计。一个超级保守的估计将设置OPT = k,这有效地假设种子集仅激活自己。但这意味着我们创建了太多的RRS集或运行了太多的蒙特卡洛模拟,因此理想情况下,我们希望有一个更好的估计/更严格的下限。
但是让事情变得更加棘手的是,事实证明,找出更严格的下限本身就是一个计算密集型过程,因此,在想要创建更少的RRS和不想浪费计算资源之间进行权衡往往是一种折衷。证明减少RRS所需的最佳OPT水平。最近的许多文献都致力于解决这个问题(参见Tang等人(2014),Tang等人(2015),Nguyen等人(2016)和Huang等人(2017)等)。除了承认它们存在之外,我们在本文中不会涉及这些复杂性。从这里开始,我们将设置较大的mc值,并希望它们获得大致相同的ϵ。
#run algorithm
celf_output = celf(df,10,p = 0.1,mc = 10000)
ris_output = ris(df,10,p = 0.1,mc = 10000)
下图比较了随着种子集大小的增长,两种算法的速度。最明显的一点是RIS算法要快得多(大约一个数量级)。该图的另一个特征是CELF的计算时间与种子集的大小成比例地增长(尽管不完全相同,请参阅上一篇文章以了解原因),而RIS算法的时间相对于种子大小保持相当恒定种子集。这是因为CELF算法必须在迭代过程的每一轮中为给定的潜在种子节点计算边际增益。相反,RIS“预先”执行所有模拟,因此扩展种子集的唯一成本是找到列表中最频繁出现的节点的“搜索成本”,这是一项相对便宜的计算工作。
# Plot
fig = plt.figure(figsize=(9,6))
ax = fig.add_subplot(111)
ax.plot(range(1,len(celf_output[1])+1),ris_output[1],label="RIS",color="#FBB4AE",lw=4)
ax.plot(range(1,len(celf_output[1])+1),celf_output[1],label="CELF",color="#B3CDE3",lw=4)
ax.legend(loc=2)
plt.ylabel('Computation Time (Seconds)')
plt.xlabel('Size of Seed Set')
plt.title('Computation Time')
plt.tick_params(bottom = False, left = False)
plt.show()
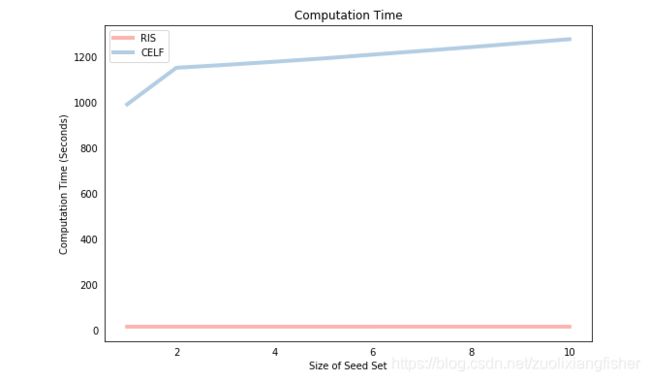
如前所述,唯一的保证是这两种方法都将产生至少达到最佳散布的(1-1 / e-1)≈63%的解决方案,这为产生不同解决方案的方法留下了很大的空间。 据我所知,尚未对方法进行系统的比较,以找出哪种方法在经验上以及在什么条件下都能实现出色的传播。 下面,我们首先打印每种方法产生的种子集,这些种子集虽然有所不同,但显示出一些重叠。 然后,我们通过IC传播函数运行每个种子集,这表明它们也实现了大致相同的传播。
# Print resulting seed set solutions
print("CELF Seed Set: %s" %celf_output[0])
print("RIS Seed Set: %s" %ris_output[0])
# Compute the spread of each seed set
celf_spread = IC(df,celf_output[0],0.1,mc=10000)
ris_spread = IC(df,ris_output[0],0.1,mc=10000)
# Print resulting spread
print("\nCELF Spread: %s" %celf_spread)
print("RIS Spread: %s" %ris_spread)
CELF Seed Set: [22, 28, 41, 69, 70, 75, 81, 82, 91, 93]
RIS Seed Set: [22, 27, 28, 34, 40, 42, 48, 89, 90, 93]
CELF Spread: 13.328
RIS Spread: 13.3285
在上面的特定示例中,RIS的传播略高,但这是由于随机性造成的。 如果我们重复相同的分析,则“最佳”方法将发生变化,但将保持在13.3区域附近。
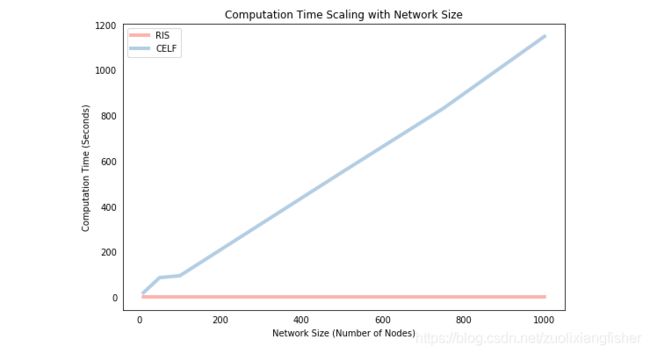
上面的速度比较显示了每种算法如何相对于种子集的大小进行缩放。 最后,我们将展示它们如何根据网络规模进行扩展。 下面,我们为每种算法求解不同的网络大小(通过调整一些参数以节省时间),并针对网络中的节点数绘制计算时间。 同样,我们发现CELF与网络规模大致成线性比例关系,而RIS在这些小规模下对网络规模几乎无所谓。
CELF_TIME, RIS_TIME, SIZES = [], [], [10,50,100,500,750,1000]
for n in SIZES:
# Generate Graph
G = Graph.Barabasi(n=n,m=3,directed=True)
# Transform into dataframe of edges
source_nodes = [edge.source for edge in G.es]
target_nodes = [edge.target for edge in G.es]
df = pd.DataFrame({
'source': source_nodes,'target': target_nodes})
# Run algorithms
celf_output = celf(df,5,p=0.1,mc=1000)
ris_output = ris(df,5,p=0.1,mc=1000)
# Store
CELF_TIME.append(celf_output[1][-1])
RIS_TIME.append(ris_output[1][-1])
# Plot computation time with respect to network size
fig = plt.figure(figsize=(9,6))
ax1 = fig.add_subplot(111)
ax1.plot(SIZES, RIS_TIME, label="RIS", color="#FBB4AE",lw=4)
ax1.plot(SIZES, CELF_TIME, label="CELF", color="#B3CDE3",lw=4)
ax1.legend(loc=2)
plt.ylabel('Computation Time (Seconds)')
plt.xlabel('Network Size (Number of Nodes)')
plt.title('Computation Time Scaling with Network Size')
plt.tick_params(bottom = False, left = False)
plt.show()
结论
我们将CELF和RIS算法都实现为简单的Python函数,并显示了以下内容:
两种算法都会产生相似的种子集并影响传播。
RIS算法的运行速度快得多,并且随着网络大小和种子集大小的增加,伸缩性也更好。