C++/PCL:最小二乘拟合平面直线,平面多项式曲线,空间多项式曲线
最小二乘原理
//fitting.h
#include
#include
#include
#include
#include
#include
#include
using namespace std;
using namespace pcl;
using namespace Eigen;
typedef PointXYZ PointT;
class fitting
{
public:
fitting();
~fitting();
void setinputcloud(PointCloud::Ptr input_cloud);//点云输入
void grid_mean_xyz(double x_resolution,double y_resolution, vector&x_mean, vector &y_mean, vector&z_mean, PointCloud::Ptr &new_cloud);//投影至XOY,规则格网,求每个格网内点云坐标均值
void grid_mean_xyz_display(PointCloud::Ptr new_cloud);//均值结果三维展示
void line_fitting(vectorx, vectory, double &k, double &b);//y=kx+b
void polynomial2D_fitting(vectorx, vectory, double &a, double &b, double &c);//y=a*x^2+b*x+c;
void polynomial3D_fitting(vectorx, vectory, vectorz, double &a, double &b, double &c);//z=a*(x^2+y^2)+b*sqrt(x^2+y^2)+c
void polynomial3D_fitting_display(double step_);//三维曲线展示
void display_point(vectorvector_1,vectorvector_2);//散点图显示
void display_line(vectorvector_1, vectorvector_2, double c, double b, double a = 0);//拟合的平面直线或曲线展示
private:
PointCloud::Ptr cloud;
PointT point_min;
PointT point_max;
double a_3d;
double b_3d;
double c_3d;
double k_line;
double b_line;
};
//fitting.cpp
#include "fitting.h"
fitting::fitting()
{
}
fitting::~fitting()
{
cloud->clear();
}
void fitting::setinputcloud(PointCloud::Ptr input_cloud){
cloud = input_cloud;
getMinMax3D(*input_cloud, point_min, point_max);
}
void fitting::grid_mean_xyz(double x_resolution, double y_resolution, vector&x_mean, vector &y_mean, vector&z_mean, PointCloud::Ptr &new_cloud){
if (y_resolution<=0)
{
y_resolution=point_max.y - point_min.y;
}
int raster_rows, raster_cols;
raster_rows = ceil((point_max.x - point_min.x) / x_resolution);
raster_cols = ceil((point_max.y - point_min.y) / y_resolution);
vectoridx_point;
vector>>row_col;
vector>col_;
vectorvector_4;
vector_4.resize(4);
col_.resize(raster_cols, vector_4);
row_col.resize(raster_rows, col_);
int point_num = cloud->size();
for (int i_point = 0; i_point < point_num; i_point++)
{
int row_idx = ceil((cloud->points[i_point].x - point_min.x) / x_resolution) - 1;
int col_idx = ceil((cloud->points[i_point].y - point_min.y) / y_resolution) - 1;
if (row_idx < 0)row_idx = 0;
if (col_idx < 0)col_idx = 0;
row_col[row_idx][col_idx][0] += cloud->points[i_point].x;
row_col[row_idx][col_idx][1] += cloud->points[i_point].y;
row_col[row_idx][col_idx][2] += cloud->points[i_point].z;
row_col[row_idx][col_idx][3] += 1;
}
PointT point_mean_tem;
for (int i_row = 0; i_row < row_col.size(); i_row++)
{
for (int i_col = 0; i_col < row_col[i_row].size(); i_col++)
{
if (row_col[i_row][i_col][3] != 0)
{
double x_mean_tem = row_col[i_row][i_col][0] / row_col[i_row][i_col][3];
double y_mean_tem = row_col[i_row][i_col][1] / row_col[i_row][i_col][3];
double z_mean_tem = row_col[i_row][i_col][2] / row_col[i_row][i_col][3];
x_mean.push_back(x_mean_tem);
y_mean.push_back(y_mean_tem);
z_mean.push_back(z_mean_tem);
point_mean_tem.x = x_mean_tem;
point_mean_tem.y = y_mean_tem;
point_mean_tem.z = z_mean_tem;
new_cloud->push_back(point_mean_tem);
}
}
}
}
void fitting::grid_mean_xyz_display(PointCloud::Ptr new_cloud){
visualization::PCLVisualizer::Ptr view(new visualization::PCLVisualizer("分段质心拟合"));
visualization::PointCloudColorHandlerCustomcolor_1(new_cloud, 255, 0, 0);
view->addPointCloud(new_cloud, color_1, "11");
view->setPointCloudRenderingProperties(visualization::PCL_VISUALIZER_POINT_SIZE, 3, "11");
PointCloud::Ptr new_cloud_final(new PointCloud);
for (int i_point = 0; i_point < cloud->size(); i_point++)
{
PointT tem_point;
tem_point.x = cloud->points[i_point].x;
tem_point.y = cloud->points[i_point].y;
tem_point.z = cloud->points[i_point].z;
new_cloud_final->push_back(tem_point);
}
view->addPointCloud(new_cloud_final, "22");
view->spin();
}
void fitting::line_fitting(vectorx, vectory, double &k, double &b){
MatrixXd A_(2, 2), B_(2, 1), A12(2, 1);
int num_point = x.size();
double A01(0.0), A02(0.0), B00(0.0), B10(0.0);
for (int i_point = 0; i_point < num_point; i_point++)
{
A01 += x[i_point] * x[i_point];
A02 += x[i_point];
B00 += x[i_point] * y[i_point];
B10 += y[i_point];
}
A_ << A01, A02,
A02, num_point;
B_ << B00,
B10;
A12 = A_.inverse()*B_;
k = A12(0, 0);
b = A12(1, 0);
}
void fitting::polynomial2D_fitting(vectorx, vectory, double &a, double &b, double &c){
MatrixXd A_(3, 3), B_(3, 1), A123(3, 1);
int num_point = x.size();
double A01(0.0), A02(0.0), A12(0.0), A22(0.0), B00(0.0), B10(0.0), B12(0.0);
for (int i_point = 0; i_point < num_point; i_point++)
{
A01 += x[i_point];
A02 += x[i_point] * x[i_point];
A12 += x[i_point] * x[i_point] * x[i_point];
A22 += x[i_point] * x[i_point] * x[i_point] * x[i_point];
B00 += y[i_point];
B10 += x[i_point] * y[i_point];
B12 += x[i_point] * x[i_point] * y[i_point];
}
A_ << num_point, A01, A02,
A01, A02, A12,
A02, A12, A22;
B_ << B00,
B10,
B12;
A123 = A_.inverse()*B_;
a = A123(2, 0);
b = A123(1, 0);
c = A123(0, 0);
}
void fitting::polynomial3D_fitting(vectorx, vectory, vectorz, double &a, double &b, double &c){
int num_point = x.size();
MatrixXd A_(3, 3), B_(3, 1), A123(3, 1);
double A01(0.0), A02(0.0), A12(0.0), A22(0.0), B00(0.0), B10(0.0), B12(0.0);
for (int i_point = 0; i_point < num_point; i_point++)
{
double x_y = sqrt(pow(x[i_point], 2) + pow(y[i_point], 2));
A01 += x_y;
A02 += pow(x_y, 2);
A12 += pow(x_y, 3);
A22 += pow(x_y, 4);
B00 += z[i_point];
B10 += x_y * z[i_point];
B12 += pow(x_y, 2) * z[i_point];
}
A_ << num_point, A01, A02,
A01, A02, A12,
A02, A12, A22;
B_ << B00,
B10,
B12;
A123 = A_.inverse()*B_;
line_fitting(x, y, k_line, b_line);
a = A123(2, 0);
b = A123(1, 0);
c = A123(0, 0);
c_3d = c;
b_3d = b;
a_3d = a;
}
void fitting::polynomial3D_fitting_display(double step_){
PointT point_min_, point_max_;
getMinMax3D(*cloud, point_min_, point_max_);
//利用最小外包框的x值,向拟合的直线做垂足,垂足的交点即为三维曲线的端点值***********
int idx_minx, idx_maxy;//x取到最大值和最小值的点号索引
for (int i_point = 0; i_point < cloud->size();i_point++)
{
if (cloud->points[i_point].x == point_min_.x) idx_minx = i_point;
if (cloud->points[i_point].x == point_max_.x) idx_maxy = i_point;
}
float m_min = cloud->points[idx_minx].x + k_line*cloud->points[idx_minx].y;
float m_max = cloud->points[idx_maxy].x + k_line*cloud->points[idx_maxy].y;
float x_min = (m_min - b_line*k_line) / (1 + k_line*k_line);
float x_max= (m_max - b_line*k_line) / (1 + k_line*k_line);
//---------------------------------------------------------------------------------------
vectorxx, yy, zz;
int step_num = ceil((x_max - x_min) / step_);
vtkSmartPointer points = vtkSmartPointer::New();
for (int i_ = 0; i_ < step_num + 1; i_++)
{
double tem_value = x_min + i_*step_;
if (tem_value>x_max)
{
tem_value = x_max;
}
xx.push_back(tem_value);
yy.push_back(k_line*xx[i_] + b_line);
double xxyy = sqrt(pow(xx[i_], 2) + pow(yy[i_], 2));
zz.push_back(c_3d + b_3d*xxyy + a_3d*pow(xxyy, 2));
points->InsertNextPoint(xx[i_], yy[i_], zz[i_]);
}
vtkSmartPointer polyLine = vtkSmartPointer::New();
vtkSmartPointer polyData = vtkSmartPointer::New();
vtkSmartPointer cells = vtkSmartPointer::New();
polyData->SetPoints(points);
polyLine->GetPointIds()->SetNumberOfIds(points->GetNumberOfPoints());
for (unsigned int i = 0; i < points->GetNumberOfPoints(); i++)
polyLine->GetPointIds()->SetId(i, i);
cells->InsertNextCell(polyLine);
polyData->SetLines(cells);
visualization::PCLVisualizer::Ptr viewer(new visualization::PCLVisualizer("最后拟合的多项式曲线"));
viewer->addModelFromPolyData(polyData, "1");
//*******************************************
PointCloud::Ptr tem_point(new PointCloud);
for (int i = 0; i < xx.size(); i++)
{
PointT point_;
point_.x = xx[i];
point_.y = yy[i];
point_.z = zz[i];
tem_point->push_back(point_);
}
visualization::PointCloudColorHandlerCustomcolor1(tem_point, 255, 0, 0);
viewer->addPointCloud(tem_point, color1, "point1");
viewer->setPointCloudRenderingProperties(visualization::PCL_VISUALIZER_POINT_SIZE, 3, "point1");
PointCloud::Ptr tem_point1(new PointCloud);
for (int i = 0; i < cloud->size(); i++)
{
PointT point_1;
point_1.x = cloud->points[i].x;
point_1.y = cloud->points[i].y;
point_1.z = cloud->points[i].z;
tem_point1->push_back(point_1);
}
viewer->addPointCloud(tem_point1, "orginal");
viewer->setPointCloudRenderingProperties(visualization::PCL_VISUALIZER_POINT_SIZE, 2, "orginal");
//显示端点
PointCloud::Ptr duandian_point(new PointCloud);
duandian_point->push_back(tem_point->points[0]);
duandian_point->push_back(tem_point->points[tem_point->size() - 1]);
visualization::PointCloudColorHandlerCustomcolor2(duandian_point, 0, 255, 255);
viewer->addPointCloud(duandian_point, color2, "duandian");
viewer->setPointCloudRenderingProperties(visualization::PCL_VISUALIZER_POINT_SIZE, 5, "duandian");
cout << "端点值1为:" << "X1= " << duandian_point->points[0].x << ", " << "Y1= " << duandian_point->points[0].y << ", " << "Z1= " << duandian_point->points[0].z << endl;
cout << "端点值2为:" << "X2= " << duandian_point->points[1].x << ", " << "Y2= " << duandian_point->points[1].y << ", " << "Z2= " << duandian_point->points[1].z << endl;
cout << "空间多项式曲线方程为: " << "z=" << a_3d << "*(x^2+y^2)+" << b_3d << "*sqrt(x^2+y^2)+" << c_3d << endl;
viewer->spin();
//拟合曲线+端点值+散点图二维平面展示,有需要可以取消注释----------------------------------------------------------
/*vectorvector_1, vector_2, vector_3, vector_4;
vector_1.push_back(duandian_point->points[0].x);
vector_1.push_back(duandian_point->points[1].x);
vector_2.push_back(duandian_point->points[0].y);
vector_2.push_back(duandian_point->points[1].y);
for (int i = 0; i < cloud->size();i++)
{
vector_3.push_back(cloud->points[i].x);
vector_4.push_back(cloud->points[i].y);
}
std::vector func1(2, 0);
func1[0] = b_line;
func1[1] = k_line;
visualization::PCLPlotter *plot_line1(new visualization::PCLPlotter);
plot_line1->addPlotData(func1, vector_1[0], vector_1[1]);
plot_line1->addPlotData(vector_3, vector_4, "display", vtkChart::POINTS);//X,Y均为double型的向量
plot_line1->addPlotData(vector_1, vector_2, "display", vtkChart::POINTS);//X,Y均为double型的向量
plot_line1->setShowLegend(false);
plot_line1->plot();*/
}
void fitting::display_point(vectorvector_1, vectorvector_2){
visualization::PCLPlotter *plot_line1(new visualization::PCLPlotter);
plot_line1->addPlotData(vector_1, vector_2, "display", vtkChart::POINTS);//X,Y均为double型的向量
plot_line1->setShowLegend(false);
plot_line1->plot();
}
void fitting::display_line(vectorvector_1, vectorvector_2,double c, double b, double a){
visualization::PCLPlotter *plot_line1(new visualization::PCLPlotter);
std::vector func1(3, 0);
func1[0] = c;
func1[1] = b;
func1[2] = a;
plot_line1->addPlotData(func1, point_min.x, point_max.x);
plot_line1->addPlotData(vector_1, vector_2, "display", vtkChart::POINTS);//X,Y均为double型的向量
plot_line1->setShowLegend(false);
plot_line1->plot();
}
//主函数
#include
#include "fitting.h"
using namespace std;
using namespace pcl;
using namespace Eigen;
typedef PointXYZ PointT;
int main() {
PointCloud::Ptr cloud(new PointCloud);
string ss("C:\\Users\\admin\\Desktop\\TEST22.pcd");
io::loadPCDFile(ss, *cloud);
vectorX, Y, Z;
for (int i_point = 0; i_point < cloud->size(); i_point++)
{
X.push_back(cloud->points[i_point].x);
Y.push_back(cloud->points[i_point].y);
Z.push_back(cloud->points[i_point].z);
}
vectorx_mean, y_mean, z_mean;
PointCloud::Ptr point_mean(new PointCloud);
double a, b, c,k_line, b_line;
fitting fit_;
fit_.setinputcloud(cloud);//点云输入
fit_.line_fitting(X, Y, k_line, b_line);//直线拟合
fit_.display_line(X, Y, b_line, k_line);//显示拟合的直线,必须先输入常量
fit_.polynomial2D_fitting(X, Z, a, b, c);
fit_.display_line(X, Z, c, b, a);//显示拟合的平面多项式曲线,输入顺序为 常量,一阶系数,二阶系数
fit_.grid_mean_xyz(0.5, -1, x_mean, y_mean, z_mean, point_mean);//0.5表示x方向的步长,-1(小于0就行)表示y方向不分段,如需分段,则设置相应步长
fit_.grid_mean_xyz_display(point_mean);//展示均值结果
fit_.display_point(X, Y);//显示散点
fit_.display_point(x_mean, y_mean);//显示均值散点
fit_.polynomial3D_fitting(x_mean, y_mean, z_mean, a, b, c);//用分段质心的均值去拟合3维曲线
//fit_.polynomial3D_fitting(X, Y, Z, a, b, c);//直接拟合
fit_.polynomial3D_fitting_display(0.5);//三维曲线展示
return 0;
}
运行结果:
1.点云XOY平面直线拟合

放大后:
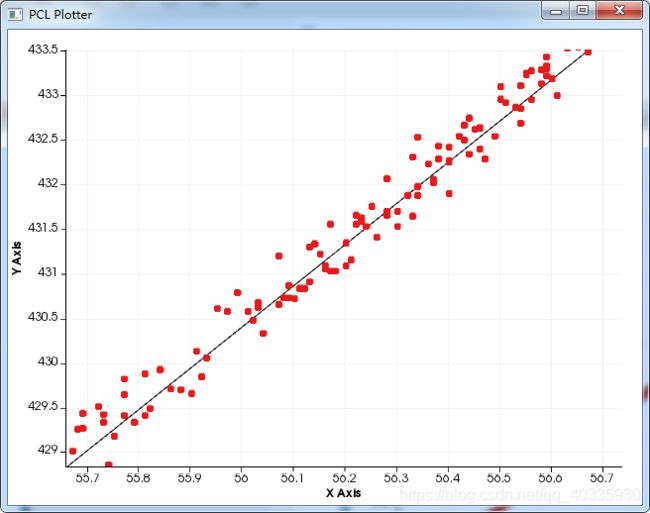
2. 平面多项式拟合

3. 分段质心展示
![]()
放大后,可以用分段质心结果去进行后续拟合:
![]()
4. 散点图:

分段质心:
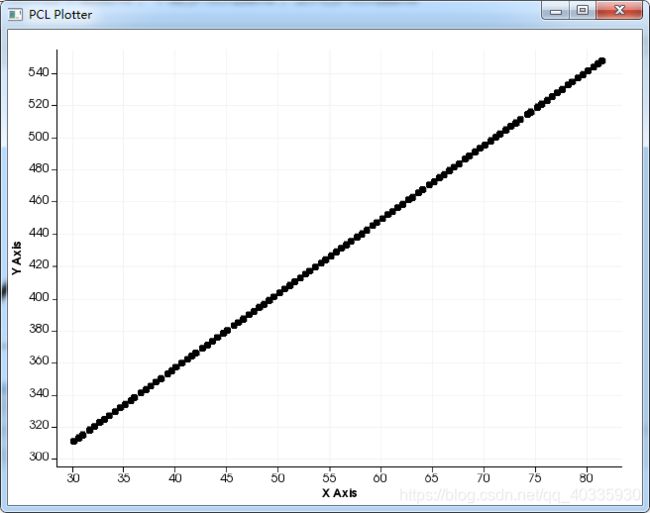
5. 空间多项式拟合结果
![]()
放大后:
![]()
蓝色点为端点:
![]()

拟合方程和端点值(只做了三维点的输出,其他方程自己看一下就好):

问题:先记录一下:
过短的线,拟合出来有问题…后续解决