关于双数组字典树ac自动机递归版实现的理解
关于双数组字典树ac自动机递归版实现的理解
字典树
简介:
字典树又名单词查找树是一种结构简单好用的树型结构:电影应用是用于统计,排序和保存大量字符串,优点是利用字符串公共祖先减少查询时间,减少无所谓的字符串比较
树形结构
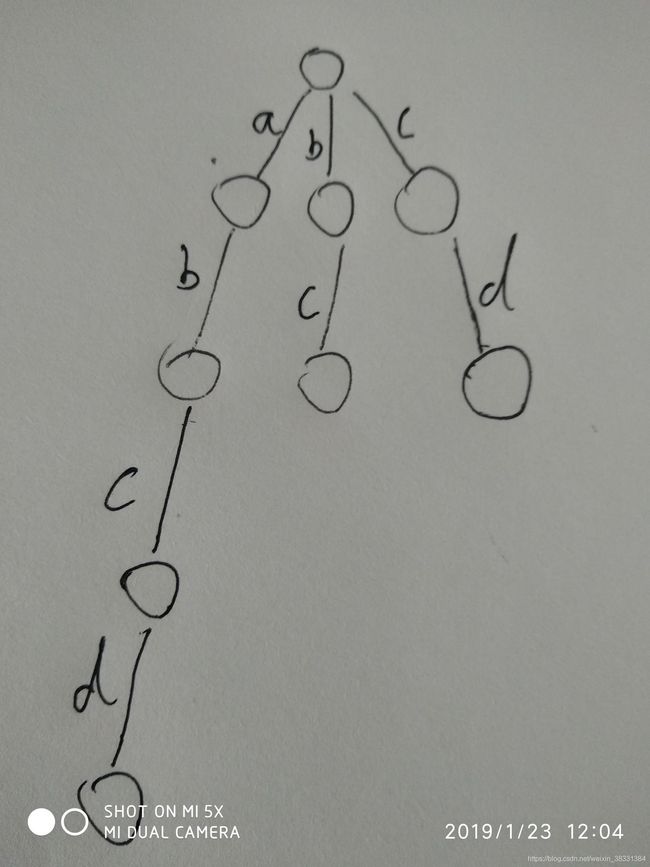
树形结构的点代表的是集合,边代表的是关系,而在字典树中,字符对应的是边,节点则是链接上一个字符和这个字符的关系,是字符构成单词的关键.如图所示
结构定义
#define BASE 'a'
#define SIZE 26
typedef struct Node{
int flag;
struct Node *next[SIZE];
}Node;
解释
flag表示的从根节点到这个节点是否有独立成次的节点,如果有就标记成1,没有则为0
struct Node *next[SIZE]是26个英文字母的指针,指向26个儿子节点
创建新的节点
Node *getNewNode() {
return (Node *)calloc(sizeof(Node), 1);
}
插入操作
int insert(Node *node, const char *str) {
Node *p = node;
int cnt = 0,ind = 0;
while (str[0]) {
ind = str[0] - BASE;
if (p->next[ind] == NULL) {
p->next[ind] = getNewNode();
cnt++;
}
p = p->next[ind];
str++;
}
p->flag= 1;
return cnt;
}
解释
str是一个字符指针,最后一位是0作为结束字符,所以我们可以用它来作为while的循环条件
ind获取相应的儿子下边,如果没有这个儿子节点我们就申请一个空间,然后指针后移,如果有,我们就直接后移.
最后当一个单词查找完成之后我们让最后一个节点的flag为1,表示从跟节点到这个节点的一条支路上存在一个单词
cnt为计数器表示又申请了多少个节点空间
查找操作
int search(Node *node, const char *str) {
Node *p = node;
int ind = 0;
while (p && str[0]) {
ind = str[0] - BASE;
p=p->next[ind];
str++;
}
return (p && p->flag);
解释
我们沿着str这条路在字典树的走,,如果p为空或者str走到尽头的时候进行返回
返回值如果p不为空并且p->flag为1时存在这个单词,其他情况均不存在
回收操作
void clear(Node *node) {
if (node == NULL) return ;
for (int i = 0; i < BASE; i++) {
clear(node->next[i]);
}
free(node);
return ;
}
解释
所有节点指针进行回收
测试程序
int main() {
Node *root = getNewNode();
int n = 0;
char str[50];
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%s", str);
insert(root,str);
}
while (scanf("%s", str)) {
printf("search %s = %d\n", str,search(root, str));
}
clear(root);
return 0;
}
双数组字典树
简介
双数组字典树与一般的字典树指示在存储结构上不同,理论结构上一样的.由原来的依靠指针寻找儿子节点位置的方式变成了计算寻找.用双数组存储字典树的原因是应为我们一般的字典树存储儿子节点都需要申请一个拥有26个儿子节点指针的新的节点,而我们往往只是用到了其中的几个.所以用双数组的方式取存储的化利用效率比较高
双数组有一个base数组和check数组,base数组存储的是用来寻找儿子节点位置信息.例如父亲节点的下标是ind 则儿子节点的下标可以是arr[ind].base + i (0arr[ind].base + i 为下标的节点是不是他的孩子所以我们就还需要一个数组用来存储儿子节点的父亲下标就是check数组 如果 arr[arr[ind].base + i].check == ind则证明他是ind号下标的一个儿子节点,那么我们怎能比表示独立成词呢,这个方法有几种,你可以在申请一个数组用来记录以ind为下标的节点是不是单独成词,当然还有一个更加巧妙的方法,我们的数字都是有正负之分的,所以当check位负数时证明形成了以这个节点为止的单词,同事判断他是不是父亲节点的儿子就改成了abs(arr[arr[ind].base + i].check) == ind
结构定义
typedef struct DANode{
int base,check;
}DANode;
申请数组
DANode *getNewDANode(int n){
return (DANode *)calloc(sizeof(DANode), n);
}
将字典树转换成一颗双数组字典树操作
//获取base值,先看下面的
int get_base(Node *node, DANode *data) {
int base = 1,flag = 0;
while (!flag) {
base++;
flag = 1;
for (int i = 0; i < SIZE; i++) {
if (node->next[i] == NULL) continue;//没有这个儿子节点返回
if (data[base + i].check == 0) continue;//没有信息返回
//运行到这一行的条件是,有data[base + i].check 有信息也就是有父亲节点
//所以我们把flag置为0,当flag位0时表示可以进行下一次循环,然后我们跳出for循环
//因为已经没有必要继续下去了,以这个base为下标的不能存储所有儿子节点
flag = 0;
break;
}
}
return base;
}
void build(Node *node, DANode * data, int ind) {
if(node == NULL) return ;
if (node->flag) data[ind].check = -data[ind].check;
//表示儿子独立成词
data[ind].base = get_base(node, data);
for (int i = 0; i < SIZE; i++) {
if (node->next[i] == NULL) continue;
data[data[ind].base + i].check = ind;
//儿子节点记录父亲节点的下标信息
}
for (int i = 0; i < SIZE; i++) {
if (node->next[i] == NULL) continue;
build(node->next[i],data,data[ind].base + i);
}
return ;
}
查找操作
int searchD(DANode *data, const char *str) {
int p = 1;
for (int i = 0; str[i]; i++) {
int delta = str[i] - BASE;
//节点是那个字符的信息
int check = abs(data[data[p].base + delta].check);
//儿子节点的父亲
if (check - p) return 0;
//如果父亲是这个节点的儿子,则check等于p,if条件位0,
p = data[p].base + delta;
//坐标后移
}
return data[p].check < 0;
}
注意事项
我们的base值最小为2,0号下标不存储东西,1号下标只用来存储跟节点,1号数组的check为0
测试程序
int main() {
Node *root = getNewNode();
int n = 0,cnt1 = 1;
char str[50];
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%s", str);
cnt1 += insert(root,str);
}
DANode *trie = getNewDANode(cnt1 * 10);
build(root,trie,1);
while (scanf("%s", str)) {
printf("search %s = %d\n", str, searchD(trie, str));
}
clear(root);
return 0;
}
ac自动机-层序实现
ac自动机是在字典树的基础上添加了一个失败指针,指向等价的节点位置,用来防止匹配失败时的文本串回退.与kmp的next数组相仿.跟节点的失败指针位空,第一层的失败指针一定指向跟节点,
结构定义
typedef struct Node{
int flag;
struct Node *next[SIZE],*fail;
}Node;
fail指针的建立
void build_ac(Node *root) {
#define MAX_N 1000
if (root == NULL) return ;
Node **queue = (Node **)malloc(sizeof(Node*) * MAX_N);
//用来存储每一层的节点,因为可能有多次回退失败指针的情况,所以在建立下一层失败指针的时候,本层的失败指针一定要建立,用层序遍历来实现比较方便
int head = 0,tail = 0;
queue[tail++] = root;
while (head < tail) {
Node *new_node = queue[head++];
//出队
for (int i = 0; i < SIZE; i++) {
if (new_node->next[i] == NULL) continue;
//没有子孩子返回
Node *p = new_node->fail;
//有子孩子,换出他的失败指针
while (p && p->next[i] == NULL) p = p->fail;
//向上寻找看是否有等价节点有这个字符的孩子,直到根节点为止
if (p == NULL) new_node->next[i]->fail = root;
//如果没有让这个孩子节点的失败指针指向跟
else new_node->next[i]->fail = p->next[i];
//如果存在让孩子的节点的失败指针,指向p相应的孩子
queue[tail++] = new_node->next[i];
//入队
}
}
#undef MAX_N
return ;
}
字符串中的查找
int search_ac(Node *root, const char *str) {
if(root == NULL) return 0;
Node *p = root;
int cnt = 0;
for (int i = 0; str[i]; i++) {
while (p && p->next[str[i] - BASE] == NULL) p = p->fail;
//看这个节点或者这个节点的等价节点有没有这个孩子
if(p == NULL) p = root;
//如果没有,则返回根节点
else p = p->next[str[i] - BASE];
//如果有p向下匹配
Node *q = p;
while (q) {
//遍历失败指针向上寻找,看是否存在有着相同后缀的字符串独立成词
cnt += q->flag;
q = q->fail;
}
}
return cnt;
}
测试程序
int main() {
Node *root = getNewNode();
int n = 0;
char str[50];
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%s", str);
insert(root,str);
}
build_ac(root);
while (scanf("%s", str)) {
printf("search %s = %d\n", str, search_ac(root, str));
}
clear(root);
return 0;
}
ac自动机-递归实现
推导思路
先正常推导递归版思路
- 首先我们接受一个节点,就去建立他儿子节点的失败指针,可以得到如下代码
void build_automaton(TrieNode *node) {
if (node == NULL) return ;
//如果节点为空返回
for (int i = 0; i < SIZE; i++) {
if (node->next[i] == NULL) continue;
//如果他没有这个孩子结束本次循环
Node *p = node->fail;//他的的失败指针
while (p && p->next[i] == NULL) {
//看他失败指针有没有这个孩子,没有就递归沿着失败指针向上找
p = p->fail;
}
if (p == NULL) p = root;
//代表没找到则失败指针位跟节点
else p = p->next[i];
//找到了他的失败指针就是p相应位置的孩子
node->next[i]->fail = p;
//失败指针赋值
build_automaton(node->next[i]);
//去建立儿子节点的失败指针
}
return ;
}
-
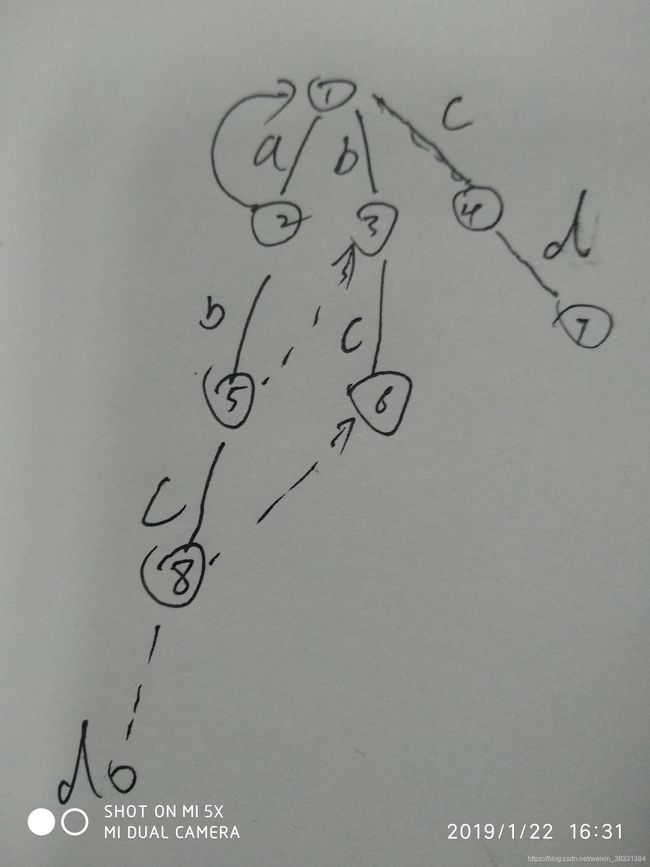
上面一个是基础版本的思路框架,但是会有几个问题?当我们沿着一条路往下走的时候,失败指针会去递归匹配失败指针的失败指针,但是我们只建立了这个分支的失败指针,其他路的失败指针我们还没有进行建立,所以我们需要跳转到那个节点去建立条支路的失败指针(如图),(当我们建立8号节点的失败指针时,6号节点下面是没有d字符的,但是从一个正常自动机的角度来说6号节点的失败指针是4,4下面有d字符)
又因为建立一个节点的失败指针是根据他的父亲节点的失败指针去建立的所以,我们个结构体添加一个父亲指针,指向他父亲的位置,用来建立连通这条支路,以便建立这条支路的失败指针,实现这些会得到一下代码
//上面解释过得代码我们就不进行解释了
void build_automaton(TrieNode *node) {
if (node == NULL) return ;
if (node->fail == NULL) build_automaton(node->father);
//先看第一步
//第二步,从第一步跳转而来,因为本条支路的所有的节点的失败指针都没有确定我们就可以
//通过这句话递归向上,找到根节点,根节点父亲节点为空,上面那个if为这个跳转的截止条件
for (int i = 0; i < SIZE; i++) {
if (node->next[i] == NULL) continue;
if (node->next[i]->fail) continue;
//第三步,因为我们一直跳到了根节点,上一次到根节点的状态与这次到根节点的状态唯一的区别呢就是,又多了一条孩子失败指针已经确立了,为了避免重复确立我们不去搜索已经确立失败指针的子孩子
//同时如果出现我们上面那个图的情况的时候,每次都遍历第一条支路,到达c节点的时候就会递归向上形成一条环路.
Node *p = node->fail;
while (p && p->next[i] == NULL) {
//第一步,如果他的失败指针的失败指针没有确立我们就确立失败指针的父亲节点
if (p->fail == NULL) build_automaton(p->father);
p = p->fail;
}
if (p == NULL) p = root;
else p = p->next[i];
node->next[i]->fail = p;
build_automaton(node->next[i]);
}
return ;
}
成环问题请看上面第三步
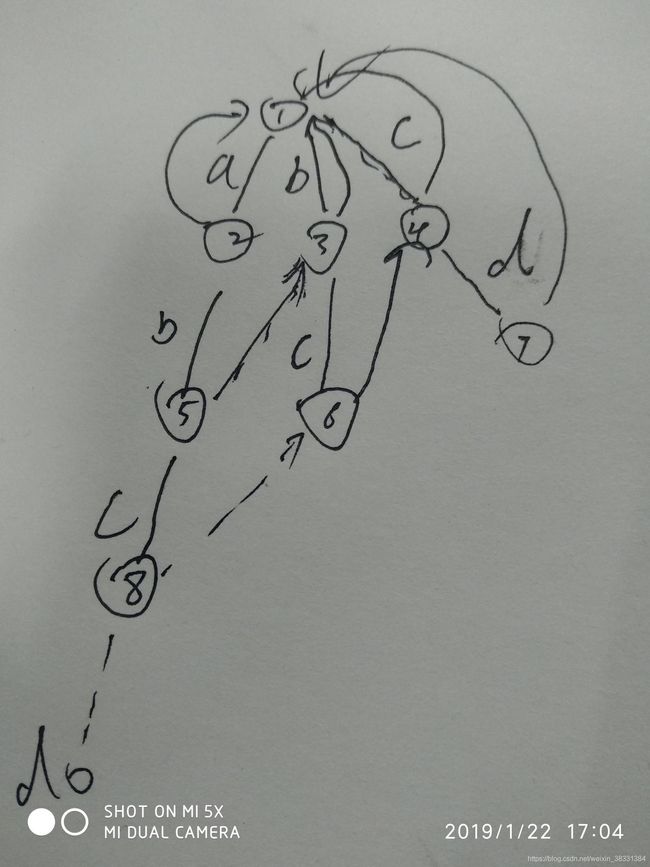
详细讨论:我们上图演示的是四层就可以形成一条环路,四层以上可不可以成环呢?
我们可以知道本层父亲节点失败指针一定是指向根节点的.所以只有两种情况一中是根节点下有那个节点,跳出while (p && p->next[i] == NULL), 二是跟节点下没有这个节点,进行递归,但是因为跟节点没有父亲节点,所以递归进去就知道被第一行的if返回了.所以跳出while (p && p->next[i] == NULL),继续向下进行,不会有成环的可能.
-
不知道你有没有注意到当节点一直递归到最上层的时候,如果没有匹配到的节点,我们就会将他的失败指针指向根节点,但是我们并没有说根节点是怎么来的,有几种可行的方案,一设立全局变量,二将根节点设置成为函数参数,三,如果匹配不成功,节点p是不断向上跳的,而且每次都去确立那一条支路的失败指针,如图所示,当第一次返回时绝大部分的失败指针都已经确定,然后就变成了非递归版的不断向上找失败时对应节点了
当完全失败周p等于NULL,则上一次p指针一定等一root,所以我们可以建立一个指针保存上一次的值
void build_automaton(TrieNode *node) {
if (node == NULL) return ;
if (node->fail == NULL) build_automaton(node->father);
for (int i = 0; i < SIZE; i++) {
if (node->next[i] == NULL) continue;
if (node->next[i]->fail) continue;
Node *p = node->fail, *pre_p = node;
//保存上一次的值
while (p && p->next[i] == NULL) {
if (p->fail == NULL) build_automaton(p->father);
pre_p = p;
//保存上一次的值
p = p->fail;
}
if (p == NULL) p = pre_p;
else p = p->next[i];
node->next[i]->fail = p;
build_automaton(node->next[i]);
}
return ;
}
双数组字典树ac自动机-层序实现
结构定义
typedef struct DANode{
int base,check,fail;
}DANode;
层序实现
int has_child(DANode *trie, int p, int i) {
return abs(trie[trie[p].base + i].check) == p;
}
//参考ac自动机层序实现
void build_ac(DANode *trie, int cnt) {
int *queue = (int *)calloc(sizeof(int), cnt + 5);
int head = 0, tail = 0;
queue[tail++] = 1;
while (head < tail) {
int now = queue[head++];
for (int i = 0; i < SIZE; i++) {
if (!has_child(trie, now, i)) continue;
int p = trie[now].fail;
while (p && !has_child(trie, p, i)) p = trie[p].fail;
if (p == 0) p = 1;
else p = trie[p].base + i;
trie[trie[now].base + i].fail = p;
queue[tail++] = trie[now].base + i;
}
}
}
匹配过程
int match(DANode *trie, const char *str) {
int cnt = 0;
int p = 1, q;
while (str[0]) {
while (p && !has_child(trie, p, str[0] - 'a')) p = trie[p].fail;
if (p == 0) p = 1;
else p = trie[p].base + str[0] - 'a';
q = p;
while (q) {
cnt += (trie[q].check < 0);
q = trie[q].fail;
}
str++;
}
return cnt;
}
双数组字典树ac自动机-递归实现
递归实现
//详情参考ac自动机递归实现推导
// 建立编号为ind节点的孩子的失败指针, 前提是编号为ind的节点失败指针已经建立了
void build_acdfs(DANode *trie,int ind) {
if(ind == 0) return ;//返回到根节点的失败指针
if(trie[ind].fail == 0) build_acdfs(trie, abs(trie[ind].check));
for (int i = 0; i < SIZE; i++) {
int childind = trie[ind].base + i;
if (!has_child(trie, ind, i)) continue;
if (trie[childind].fail) continue;//失败指针已经建立不用再次建立
int p = trie[ind].fail;
while (p && !has_child(trie, p, i)) {
if (trie[p].fail == 0) build_acdfs(trie,abs(trie[p].check));
p = trie[p].fail;
}
if (p == 0) p = 1;
else p = trie[p].base + i;
trie[childind].fail = p;
build_acdfs(trie,childind);
}
}
完整参考程序
/*************************************************************************
> File Name: 4.double_arraytree_ac_dfs.cpp
> Author: ldc
> Mail: litesla
> Created Time: 2019年01月23日 星期三 17时45分13秒
************************************************************************/
#include