NLP之---word2vec算法skip-gram原理详解

1.词嵌入（word2vec）

自然语言是一套用来表达含义的复杂系统。在这套系统中，词是表义的基本单元。顾名思义，词向量是用来表示词的向量，也可被认为是词的特征向量或表征。把词映射为实数域向量的技术也叫词嵌入（word embedding）。近年来，词嵌入已逐渐成为自然语言处理的基础知识。

2.为何不采用one-hot向量

• 【如何使用one-hot】
  • 假设词典中不同词的数量（词典大小）为$N$，每个词可以和从0到$N-1$的连续整数一一对应。这些与词对应的整数叫作词的索引。
  • 假设一个词的索引为$i$，为了得到该词的one-hot向量表示，我们创建一个全0的长为$N$的向量，并将其第$i$位设成1。这样一来，每个词就表示成了一个长度为$N$的向量，可以直接被神经网络使用。
  • 简单来说：就是有多少个不同的词，我就会创建多少维的向量，如上：一个词典中有$N$个不同词，那么就会开创$N$维的向量，其中单词出现的位置为以1，该位置设为$i$，那么对应的向量就生成了。举个例子：[我，喜，欢，学，习]，其中的“我”就可以编码为：[1,0,0,0,0]，后面的“喜”就可以编码为：[0,1,0,0,0]，依次类推。
• 【存在的问题】
  • 无法使用该方法进行单词之间的相似度计算。
  • 原因就是每个单词在空间中都是正交的向量，彼此之间没有任何联系。
  • 比如我们通过余弦相似度进行度量。
    $$\frac{{\mathbf{x}}^{\top }\mathbf{y}}{\Vert \mathbf{x}\Vert \Vert \mathbf{y}\Vert }\in [-1,1].$$
  • 对于向量$\mathbf{x},\mathbf{y}\in {\mathbb{R}}^d$，它们的余弦相似度是它们之间夹角的余弦值。
• 【解决策略】
  • 既然one-hot的方式没有办法解决，那么我们就需要通过词嵌入的方式来解决。也就是我们后面重点要讲解的word2vec的方法。该方法目前有两种实现模型。
    • 跳字模型（skip-gram）：通过中心词来推断上下文一定窗口内的单词。
    • 连续词袋模型（continuous bag of words，CBOW）：通过上下文来推断中心词。

3.跳字模型（skip-gram）

• 下面围绕着这样一幅图片进行展开。
  
• 首先我们举个栗子来说明这个算法在干嘛。
  • 假设在我们的文本序列中有5个词，[“the”，“man”，“loves”，“his”，“son”]。
  • 假设我们的窗口大小skip-window=2，中心词为“loves”，那么上下文的词即为：“the”、“man”、“his”、“son”。这里的上下文词又被称作“背景词”，对应的窗口称作“背景窗口”。
  • 跳字模型能帮我们做的就是，通过中心词“loves”，生成与它距离不超过2的背景词“the”、“man”、“his”、“son”的条件概率，用公式表示即：
    $$P(\text{“the"},\text{“man"},\text{“his"},\text{“son"}\mid \text{“loves"}).$$
  • 进一步，假设给定中心词的情况下，背景词之间是相互独立的，公式可以进一步得到：
    $$P(\text{“the"}\mid \text{“loves"})\cdot P(\text{“man"}\mid \text{“loves"})\cdot P(\text{“his"}\mid \text{“loves"})\cdot P(\text{“son"}\mid \text{“loves"}).$$
  • 上面的变换就类似于贝叶斯到朴素贝叶斯的变换过程。
  • 简单图示可以表示为：
    
  • 可以看得出来，这里是一个一对多的情景，根据一个词来推测2m个词，（m表示背景窗口的大小）。
  • 通过上面的例子大概清楚，skip-gram在做什么，那么就一步一步来解析上面的图。

3.1 one-hot word symbol（编码）

• 第一步，进行one-hot编码，有同学可以能疑惑，开篇就说了one-hot不行，存在着致命的问题，没有办法计算单词之间的相似度，但是我们不要忽略一个事实，计算机没办法识别“字符”，所有的数据必须转化成二进制的编码形式。

• 那么既然选择了使用one-hot进行编码，该怎么进行处理呢？

  • 这个其实也非常的简单，就是常规操作，相信学过机器学习的都清楚，为了扫盲下面在啰嗦一下。
  • 比如我这里的文本序列为：[“the”，“man”，“loves”，“his”，“son”]，那么可以进行如下编码了。
  • the ：[1,0,0,0,0]
  • man：[0,1,0,0,0]
  • loves：[0,0,1,0,0]
  • his：[0,0,0,1,0]
  • son：[0,0,0,0,1]

• 这样的方式非常的简单，编码后的结果就是一个非常稀疏的矩阵了。(稀疏到什么程度呢？每一行只有一个元素，其余的都为0)

• 比如：我的词典里有$N$个不重复的单词，那么整体编码后就是$N\ast N$维的一个大矩阵了，对于一个单词来说就是$1\ast N$的向量。

3.2 Lookup Table（查表）

• 上面我们说到了，one-hot是没发计算相似度，我们为了解决计算机无法识别“字符类型”的数据这一问题，又不得不使用这种方式，但是我们要清楚我们这么做是为了解决编码问题，最终的目的我们是想用一个稠密的向量去表示一个单词，并且这个单词是可以在空间中表征准确含义的。
• 比如，“man”和“woman”在空间中就应该是距离比较近的。
• 既然这样，那么我们必须先初始化一个这样的向量，然后通过学习的方式来更新向量的值（权重），然后得到我们最终想要的向量。
• 既然有这样的想法，就必须先将我们上面进行one-hot方式表示的单词，用一个稠密的向量进行表示，也就是进行一个映射。
• 这个映射过程，就被称作是嵌入(embedding)，因为是单词的映射，所以被叫做词嵌入(word embedding)，好，既然知道了要做这样的embedding，那具体该怎么去做呢？
• 假设我们要把一个单词映射到一个300维（这个300维是经过大量的实验得出的，一般的映射范围是200-500维）的向量中，那么我们直观的做法就是：矩阵运算。因为我们每个单词现在的情况是$N$维的一个向量，如果映射到300维，需要的权重矩阵就是$N\ast 300$，这样得到的矩阵就是一个$1\ast 300$的矩阵，可以理解为向量。以下图所示(假设N=5)。
  
• 矩阵的运算大家应该很清楚，后面的结果，在程序中就是通过，对应元素相乘再相加得到的，比如：$10=0\ast 17+0\ast 23+0\ast 4+1\ast 10+0\ast 11$，其他的可以依次得到。但是对于这么小的矩阵，在运算时就进行了$5\ast 3=15$次操作，如果我的词汇表中有$N=100000$个不同的单词，每个词向量的大小为300，那么一个单词的映射就会计算$N\ast 300$次，3千万次的计算，可能觉得不算什么，但是我们要清楚，词汇表的大小可不止10万，这样的计算量应该是极其庞大的。
• 细心的同学可能已经观察到了，在上图存在着一个规律：
  • 没错了，计算出来的这组向量，和我们单词在one-hot编码表的位置是有关系的！
  • 如果单词出现的位置column = 3，那么对应的就会选中权重矩阵的Index = 3，（索引从0开始），知道了这个对于我们来说意味着什么呢？
  • 到现在为止，这个问题应该已经非常清楚了，我们不必计算了，直接通过这种索引位置对应的关系就可以将单词映射到任意的维度了。
  • 上面的通过索引对应的映射方式，就是查表(LookUp Table)了，不需要计算，仅仅是通过查询就可以进行映射了。
• 理解了上面，我们就在用专业的术语描述一下：
  • 这种映射关系为单映射， 那么何为单映射呢？简单理解就是：如果集合A→集合B存在映射关系，并且集合A中任意不同的元素，在集合B中有不同的映射，这样做的目的是，保证每个单词都是独立的，都是不同的。
  • 在进行映射之后，信息量不会发生变化。
  • 过程就是，将one-hot编码后的词向量，通过一个神经网络的隐藏层，映射到一个低纬度的空间，并且没有任何激活函数。
• 好，目前为止我们已经走完了两步：one-hot → lookup table。也就完成了我们词向量的初始化，后面要做的事情就是训练。后面有点难度了！！！

3.3 数学原理（参数更新）

• 先看一个图，标明一下我们进行到哪一步了。
  
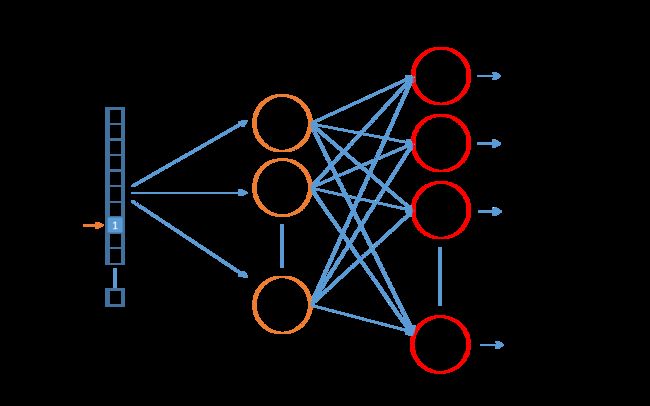
• 大家已经注意到，我们已经到了Hidden Layer到Output Layer这一层了，简单来看就是隐藏层和输出层进行全连接，然后是一个softmax，输出概率。
• 过程比较简单，一个Forward Propagation，一个Backward Propagation。完成参数的更新，为了方便理解，我们还是以一开始的例子说明一下。
• 举个例子
  • 假设文本序列是“the”“man”“loves”“his”“son”。
  • 以“loves”作为中心词，设背景窗口大小为2。如图所示，跳字模型所关心的是，给定中心词“loves”，生成与它距离不超过2个词的背景词“the”“man”“his”“son”的条件概率，即

$$P(\text{“the"},\text{“man"},\text{“his"},\text{“son"}\mid \text{“loves"}).$$

• 假设给定中心词的情况下，背景词的生成是相互独立的，那么上式可以改写成

$$P(\text{“the"}\mid \text{“loves"})\cdot P(\text{“man"}\mid \text{“loves"})\cdot P(\text{“his"}\mid \text{“loves"})\cdot P(\text{“son"}\mid \text{“loves"}).$$

• 在跳字模型中，每个词被表示成两个$d$维向量，用来计算条件概率。假设这个词在词典中索引为$i$，当它为中心词时向量表示为${\mathbf{v}}_i\in {\mathbb{R}}^d$，而为背景词时向量表示为${\mathbf{u}}_i\in {\mathbb{R}}^d$。设中心词$w_c$在词典中索引为$c$，背景词$w_o$在词典中索引为$o$，给定中心词生成背景词的条件概率可以通过对向量内积做softmax运算而得到：
• $$P(w_o\mid w_c)=\frac{\text{exp}({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)},$$
• 上面的公式还是比较容易理解的，由中心词来推断背景词，注意整个过程的输入是(中心词向量，背景词向量)，根据上面的所提到的背景词之间都是独立的，这种时候，可以把概率写成连乘的形式：
• $$\prod _{t=1}^T\prod _{-m\le j\le m,j̸=0}P(w^{(t+j)}\mid w^{(t)}),$$
• 上述公式中，T表示窗口中心词的位置，m表示的窗口的大小。这样就可以计算出每个中心词推断背景词的概率，而我们在输入的时候给出了背景词的向量，此时只需要最大化背景词的输出概率即可。 基于这样的想法，我们会想到极大化似然估计的方式。但是一个函数的最大值往往不容易计算，因此，我们可以通过对函数进行变换，从而改变函数的增减性，以便优化。
• $$-\sum _{t=1}^T\sum _{-m\le j\le m,j̸=0}\text{log}P(w^{(t+j)}\mid w^{(t)}).$$
• 上面的变换，非常容易理解：1）对数似然变换，因为对数是单调递增，不会影响原函数的单调性；2）添加负号“-”，会使得原函数的单调性对调。
• 最小化损失函数，我们最容易想到的就是梯度下降法。在使用梯度下降法之前，我们要把我们的损失函数定义出来，毕竟上面的式子是一个概率，下面吧softmax的计算结果带入得到：
• $$\log P(w_o\mid w_c)={\mathbf{u}}_o^{\top }{\mathbf{v}}_c-\log \left(\sum _{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)\right)$$
• 损失函数已经得到了，我们的目标就是最小化它，优化它之前我们要搞清楚我们的参数是谁？每错，我们的参数是中心词和背景词，那对于这样的一个函数显然是非凸函数，因此，我们要做一个假设，假设在对中心词权重更新时，背景词的权重是固定的，然后在以同样的方式来更新背景词的权重。
• 既然是梯度下降法，那么就求导计算梯度吧：
• $$\begin{array}{rl}\frac{\partial \text{log}P(w_o\mid w_c)}{\partial {\mathbf{v}}_c}& ={\mathbf{u}}_o-\frac{{\sum }_{j\in \mathcal{V}}\exp ({\mathbf{u}}_j^{\top }{\mathbf{v}}_c){\mathbf{u}}_j}{{\sum }_{i\in \mathcal{V}}\exp ({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}\\ & ={\mathbf{u}}_o-\sum _{j\in \mathcal{V}}\left(\frac{\text{exp}({\mathbf{u}}_j^{\top }{\mathbf{v}}_c)}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}\right){\mathbf{u}}_j\\ & ={\mathbf{u}}_o-\sum _{j\in \mathcal{V}}P(w_j\mid w_c){\mathbf{u}}_j.\end{array}$$
• 这里涉及到了链式法则的求导方式，不懂的同学自己补补啦！
• 这里就计算出来了中心词的梯度，可以根据这个梯度进行迭代更新。对于背景词的更新是同样的方法。但是要注意背景词的个数不是唯一的，所以更新的时候要逐个更新，幅图辅助理解。
• 下图中的第一行，中心词为“The”，对应的背景词就有2个“quick”、“brown”
• 训练结束后，对于词典中的任一索引为$i$的词，我们均得到该词作为中心词和背景词的两组词向量${\mathbf{v}}_i$和${\mathbf{u}}_i$。
• 这里存在几个问题：
  • 一个是在词典中所有的词都有机会被当做是“中心词”和“背景词”，那么在更新的时候，都会被更新一遍，这种时候该怎么确定一个词的向量到底该怎么选择呢？
    • 在自然语言处理应用中，一般使用跳字模型的中心词向量作为词的表征向量。
  • 另一个问题就比较验证了，从刚刚最终的梯度公式中，存在着一个参数$\mathcal{V}$，我们知道这个参数代表的含义是词典中单词的个数，通常这个个数会非常大，这时候我们在进行迭代的时候对系统消耗也是巨大的，因为每走一步就要对所有的单词进行一次矩阵运算。这种时候该如何进行优化呢？
    • 负采样
    • 层级softmax
    • 这两种优化方式后面介绍。

3.4 简单总结一下

• 上面已经介绍了整个skip-gram算法的过程以及原理。把我们开始的图拿过来进行梳理：

• 1.one-hot编码。每个单词形成$V\ast 1$的向量；对于整个词汇表就是$V\ast V$的矩阵。
• 2.lookup table查表降维。根据索引映射，将每个单词映射到d维空间，通过这样的方式就可以将所有的单词映射到矩阵$W$上（矩阵的形状为$V\ast d$），并且每个单词与矩阵中的某列一一对应。
• 3.skip-gram模型训练。初始化一个d维空间的矩阵作为权重矩阵$W^{\prime }$，该矩阵的形状为$V\ast d$，值得注意的是，目前我们已经有了两个d维空间的矩阵。要清楚这两个矩阵分别都是干嘛的，一个是作为中心词时的向量$v_i$，一个是作为背景词时的向量$u_i$（每个词都有机会成为中心词，同时也会成为其他中心词的背景词，因为窗口再变动）。
• 4.取出中心词的词向量$v_c$(它的形状为d维的向量$1\ast d$)，与权重矩阵$W^{\prime }$中的其他词做内积，此时会得到每个词的计算结果，即：$v_c\ast u_o^T$(假设背景词的索引为$o$)。
• 5.softmax层的映射。在上一步中得到了$V$个数字，那么此时我们需要做的就是计算每个词的概率，即：$\frac{\text{exp}({\mathbf{u}}_o^{\top }{\mathbf{v}}_c)}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}$。大家要注意此时的$i$它表示的是词典中任意的一个词。因此分母部分的计算量极其大。
• 6.概率最大化。不要忘记了此时的学习相当于监督学习了，我们是有明确的背景词输入的，我们期望窗口内的词的输出概率最大。因此我们的目标变为极大化概率$P(w_o\mid w_c)$，在不影响函数单调性的前提下我们变为极大化函数：$\log P(w_o\mid w_c)$（对数似然）,但是，我们都明白，计算一个函数的最大值不如计算一个函数的最小值来的方便，因此这里给这个函数进行单调性变换：$-\log P(w_o\mid w_c)$
• 7.极小化目标函数。通过上面的变换，此时已经变为一个数学优化问题，梯度下降法更新参数。
• 8.更新中心词的向量$v_c$，上面已经推导出结果了，$v_c:=v_c-\alpha \ast \nabla P(w_o\mid w_c)$，后面减去的即为梯度：$\nabla P(w_o\mid w_c)={\mathbf{u}}_o-{\sum }_{j\in \mathcal{V}}\left(\frac{\text{exp}({\mathbf{u}}_j^{\top }{\mathbf{v}}_c)}{{\sum }_{i\in \mathcal{V}}\text{exp}({\mathbf{u}}_i^{\top }{\mathbf{v}}_c)}\right){\mathbf{u}}_j$；**简单分析一下：大括号里面的是一个概率值，然后乘上一个矩阵(向量)$u_i$，仍然是一个矩阵，相当于对矩阵进行了加权，然后$u_o$这个背景词矩阵再减去这个加权矩阵，就得到了$v_c$的梯度值。如此给上一个学习率就可以迭代更新了。
• 9.有同学可能注意到了，这里面为什么又多了个下标$j$，这个下标代表的背景词，$j$的取值范围是$-m\le j\le m,j$不能为$0$，这么做才能与我们最初的设定相对应吧！一个中心词，推断多个背景词。
• 10.根据同样的原理，在窗口进行移动了之后，可以进行同样的更新。
• 11.在词汇表中所有的词都被训练之后。我们得到了每个词的两个词向量分别为$v_i、u_i$，$v_i$是作为中心词时的向量，我们一般用这个作为最终的选择。$u_i$对应的就是作为背景词时的向量了。

4.未完待续~~

• 本想一篇写完关于word2vec的两个算法，但是篇幅太长了。再开两篇来写CBOW和近似训练。