机器学习-多项式回归
内容简介:
1.在我们上节课所讲的一元线性回归的算法所用到的是利用最小二乘法去解决,但是最小二乘法并不适合去处理对多元线性回归进行拟合,我们将会利用矩阵的方式去解决。
基础知识:
多元线性回归公式
线性代数基础:
基本概念:
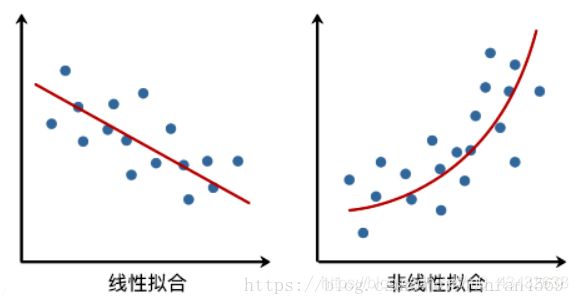在传统的一次方程进行线性拟合时候是左面的图,而当为多项式拟合是则是一条曲线右图所示，针对一元线性回归如果利用矩阵的方式如下:我们设
由一元线性公式可得
也就是说矩阵A乘以矩阵θ 等于矩阵B
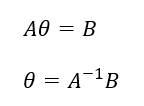
但是需要注意的是之只有当A矩阵为n阶矩阵的时候才能有可逆矩阵,所以我们需要将其公式进行变化一下
其实A^T A的目的就是为了让A变为一个n阶的矩阵有可逆矩阵当然需要和原来的等式成立
多元线性方程:
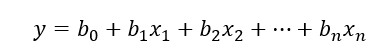
多元线高阶归方程:
多元线性方程、多元高阶方程其实也是一个道理,就是在构造A矩阵的时候需要修改,其实在sklearn里就已经有固定方法
from sklearn.preprocessing import PolynomialFeatures具体怎么使用,小伙伴们自己动手找度娘吧!
就到这里了,拜拜!