Joint Embedding Learning and Low-Rank Approximation: A Framework for Incomplete Multiview Learning
Joint Embedding Learning and Low-Rank Approximation: A Framework for Incomplete Multiview Learning (TCYB2019)
论文链接:https://ieeexplore.ieee.org/abstract/document/8920218
1 论文主要贡献
提出了一种用于不完整多视图学习的框架:Joint Embedding Learning and Low-Rank Approximation (JELLA),是目前比较流行的不完整多视图学习方法的一般形式,同时利用 JELLA 可以快速将一些多视图学习方法转化为不完整多视图学习方法,有种自适应的思想; 此外在 JELLA 下,为不完整多视图学习(IML)提出了一种 block-diagonal 表示方法。
2 论文主要内容
2.1 Introduction
Multi-view 中两种数据缺失的情况:
• missing-view setting:某些视图整个缺失 ;
• missing variables setting:某些视图中部分变量缺失。
Missing-view setting 与 missing variables setting 共同构成了 incomplete-view setting.
在传统的多视图学习算法中,通常有两种方法来处理不完整的多视图数据:
• 一种方法是丢弃不完整的示例,这会导致丢失可用信息;
• 另一种方法是用可用样本的平均值填充缺失样本,并通过传统的矩阵完成算法补充 缺失变量。这样可以保存一些有用的信息,但是仍然会产生误差
为了处理缺少视图的多视图数据,近年来提出了以下的方法(2.2 中详细介绍):
• Partial multiview clustering (PVC):仅针对 missing-view 的情况,通过 NMF 学习完整表达;
• Multiview learning with incomplete views (MVL-IVs):基于子空间学习的思想,通过 multiview matrix completion 方法恢复不完整样本;
• Incomplete multimodality grouping (IMG):将几何信息合并到表示中,并设计了 IMG 方法。 具体来说,IMG 在公共表示上强加带有自动学习图的流形正则化,以增强 分组可辨性。
• Doubly aligned incomplete multiview clustering (DAIMC):基于加权半 NMF,开发了 DAIMC 算法,同时对齐了样本和基础矩阵。
基于以上四种方法的相似之处,本文提出 JELLA 框架,引入一组低秩矩阵来近似不完整表示。如果没有丢失,则近似矩阵的项将被约束为等于原始数据矩阵的对应项。然后,采用映射函数(例如,线性变换)的概念来从多个视图中学习完整和通用的嵌入。即,通过使 用多个视图的兼容和互补信息,将近似数据矩阵映射到公共表示矩阵。
JELLA 优点:
• 将 PVC、MVL-IVs、IMG、DAIMC 统一到一个框架中;
• 在此框架的指导下,为完整的多视图数据开发的某些先前的多视图算法可以直接适 用于 IML.
2.2 JELLA

其中, X ( v ) ∈ R d ( v ) × n X^{(v)}\in \mathbb{R}^{d^{(v)}×n} X(v)∈Rd(v)×n 为第 v v v 个视图的原始数据矩阵; Z ( v ) ∈ R d ( v ) × n Z^{(v)}\in \mathbb{R}^{d^{(v)}×n} Z(v)∈Rd(v)×n 为第 v v v 个视图补全后的数据矩阵(秩为 r r r); U ( v ) ∈ R d ( v ) × r U^{(v)}\in \mathbb{R}^{d^{(v)}×r} U(v)∈Rd(v)×r 为第 v v v 个视图的转换矩阵(可以理解为映射函数); W ∈ R r × n W\in \mathbb{R}^{r×n} W∈Rr×n 为统一表达矩阵; Γ ( v ) ∈ R d ( v ) × n \Gamma ^{(v)}\in \mathbb{R}^{d^{(v)}×n} Γ(v)∈Rd(v)×n 为第 v v v 个视图的样本索引矩阵,即 X i j ( v ) X^{(v)}_{ij} Xij(v)不缺失对应 Γ i j ( v ) = 1 \Gamma ^{(v)}_{ij}=1 Γij(v)=1,否则为 0 0 0; f ( v ) ( . ) f^{(v)}(.) f(v)(.) 为loss function; R 1 ( U ( v ) ) \mathcal{R}_1(U^{(v)}) R1(U(v)) 和 R 2 ( W ) \mathcal{R}_2(W) R2(W)分别为 U ( v ) U^{(v)} U(v) 与 W W W 的正则项。第一个约束条件保证当数据不缺失时, Z Z Z 与 X X X的对应项相等; C 1 ( v ) , C 2 \mathcal{C}^{(v)}_1,\mathcal{C}_2 C1(v),C2 分别为 U ( v ) U^{(v)} U(v) 与 W W W 的约束。
如果原始矩阵 X X X 是完整的,那么就不用学习低秩矩阵 Z Z Z 了,此时 JELLA 退化为 complete multiview model. JELLA 框架能够灵活地处理不完整 or 完整多视图学习,缩小完整的多视 图学习与 IML 之间的差距。
Multiview learning 统一到 JELLA 框架中,如下图所示:

Optimization Strategy :交替优化即可

2.3 IML-BDR
BDR: Block Diagonal Regularizer. 最近的一项研究表明,具有块对角性质的方法促进正 确的子空间聚类。为了提高学习的嵌入矩阵 W W W 的可分辨性,本文引入 k-BDR 矩阵 B ∈ R n × n B\in\R^{n×n} B∈Rn×n来自我表达 W W W,即 W = W B W = WB W=WB (note: B 不是单位阵)。
Definition 1 (k-Block Diagonal Regularizer): Given a similarity matrix B ∈ R n × n B\in\R^{n×n} B∈Rn×n, the k block-diagonal regularizer is defined as the sum of the k k k smallest eigenvalues of L B L_B LB, that is,
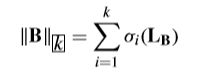
L B L_B LB是 B B B 的拉普拉斯矩阵, σ i ( L B ) \sigma_i(L_B) σi(LB) 是 L B L_B LB 的第 i i i 小的特征值;若对 L B L_B LB 施加秩约束,则图结构中的连通分量个数等于 L B L_B LB 特征值中 0 0 0 的个数。
IML-BDR 的目标函数:
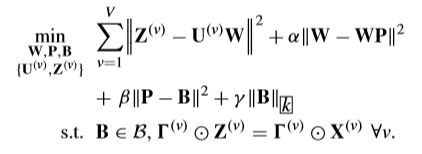
引入矩阵 P P P 保证了 P P P 和 B B B 的子问题为强凸,当 β \beta β 足够大时,Eq(3)第二项等同于 α ∣ ∣ W − W B ∣ ∣ 2 \alpha||W-WB||^2 α∣∣W−WB∣∣2; B = { B ∣ d i a g ( B ) = 0 , B = B T , B ≥ 0 } B=\left\{B|diag(B)=0,B=B^T,B\ge0\right\} B={ B∣diag(B)=0,B=BT,B≥0}.
Optimization Strategy :先借助对角矩阵分解,把 k-Block Diagonal Regularize 项转化成 凸优化,然后交替优化,直接偏导置 0 0 0 即可。
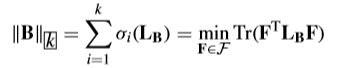
2.4 实验设置
Data sets
MSRC-v1: 240 images belonging to 8 classes, 选择其中 210 幅,7 类图像;采用 SIFT(200 维),LBP(256 维);
Yale: 165 grayscale face images of 15 individuals, 采用 SIFT (50 维), GIST (512 维) 和 LBP (256 维); Corel5k: 4999 images from 50 categories, 采用 GIST (512 维), DenseSIFT (1000 维)和 DenseHue (100 维);
Caltech101: 101 kinds of objects, 选择其中 441 幅,7 类图像;采用 SIFT (200 维), SURF (200 维)和 LBP (256 维);
Trecvid: 1078 video shots belonging to 5 categories, 采用 the text feature (1894 维)和 the HSV color histogram (165 维);
PIE: 11554 samples belonging to 68 categories, 采用 SIFT (50 维)和 LBP (256 维)。
Missing-view setting:随机选择 m m m 个百分比(10%到 50%)的示例,并从每个示例中随机丢弃一个视图;
Incomplete-view setting:第一步与 missing-view setting 相同,即随机选择 m % m% m%(10% 至 50%)的示例,并为每个示例删除一个随机视图。然后,在每个视图上,从其余示例形成的矩阵中随机删除 m % m% m%(10%到 50%)的项。
Baseline
PVC, MVL-IV, IMG, DAIMC;
MIC (Multiple incomplete views clustering via weighted non-negative matrix factorization with L 2 , 1 L_{2,1} L2,1 regularization);
iRMKMC (Multi-view K-means clustering on big data).
Evaluation
RMSE ( ↓ ↓ ↓): root-mean-square error;
NMI ( ↑ ↑ ↑): normalized mutual information;
AdjRI ( ↑ ↑ ↑): adjusted rand index.