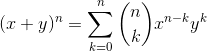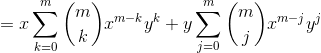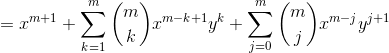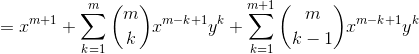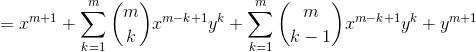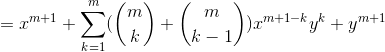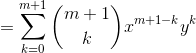数学漫谈：深入理解e

定义：数列极限

设{ }为一个无穷实数数列的集合。如果存在实数，对于任意实数（无论其有多么小），N>0，使不等式|x-|<在n(N, +)上恒成立，那么就称常数是数列{x} 的极限。

定义：戴德金分割

将一切有理数的集合划分为两个非空且不相交的子集A和A'，使得集合A中的每一个元素小于集合A'中的每一个元素。集合A称为划分的下组，集合A'称为划分的上组，并将这种划分记成A|A'。

戴德金定理

若A|A'是实数系R的戴德金分割，则由它可确定惟一实数β，若β落在A内，则它为A中最大数，若β落在A'内，则它是A'中最小数。

证明：

已知对于戴德金分割，把实数域拆分成两个均非空集A及A'，使能满足：

情形1：每一实数必落在集A或A'中的一个且仅一个之内；

情形2：集A的每一数α小于集A'的每一数α'。

将属于A的一切有理数集记成AR，属于A'的一切有理数集记成AR'，容易证明，集AR和集AR'形成有理数域内的一个分划。

这分划AR|AR'确定出某一实数β。如果β满足：∀α，α≤β，那么β属于集A，并且β是集A中的最大数。

假设：β不是集A中的最大数。那么∃γ，γ∈A，并且γ>β。那么，存在有理数η，满足：γ>η>β。这与前提矛盾。因此，β是集A中的最大数。

同理可证β属于集A'的情形。

定理：单调有界数列必有极限

证明：

设数列{x}单调递增且有上界。

第1种情形，如果{x}从第N项开始所有的项都相等，由于数列是单调递增的，当n>N时，X=X。所以，>0，|X-X|=0<。X是数列{x}的极限。

第2种情形，如果{x}只有有限项相等，那么数列从某项开始严格递增。

1.{X}，X{X}，。所以，{X}，都不是{X}的上界。

2.取集合B包含{x}的所有上界。取集合A=R/B。

3.B，A。

4.AB=R。

5.由于A中任何元素都不是{x}的上界，所以A，X{X}，。所以，集合A中不存在最大数。

6.根据戴德金定理，集合B中存在最小数β。

7.>0，NN，β-。n>N，β-。

8.n>N，X<β+。

9.n>N，|X-β|<。

10.

11.同理，单调递减数列如果存在下界，那么必有极限。

帕斯卡法则：

证明：

1.设从n个元素中取出k个元素的全部组合构成集合S。

2.对于n个元素中的某个元素x，S可以划分为集合A和集合B，A中的所有组合均不包含x，而B中的所有组合均包含x。显然：S=AB。

3.集合A等价于从不包含x的n-1个元素中取k个元素的全部组合，即：

4.集合B等价于从不包含x的n-1个元素中取k-1个元素的全部组合，即：

5.所以命题成立。

二项式定理

证明：

1.当n=1时，公式成立。

2.设当n=m时，公式成立。

3.当n=m+1时：

公式成立。

二项式定理引理

设：，，

，仅当y=0时，取等号。

证明：根据二项式定理，引理明显正确。

均值不等式定理：

证明：

1.当n=2时，公式成立。

2.设当n=k时，公式成立，即：

3.当n=k+1时：

设：是中的最大值。则：。

设：。

定理成立。

常数e存在定理1：

证明：

1.根据均值不等式定理：

所以，数列是单调递增的。

2.存在不等式：

3.根据均值不等式：

可知，4是数列的一个上界。

4.根据定理单调有界数列必有极限，可知常数e存在。

定义：函数极限

设函数在点的某一去心邻域内有定义，如果存在常数，对于任意给定的正数(无论有多么小)，总存在正数，当不等式成立时，不等式成立，那么常数就是当时函数的极限。

夹逼定理

1.对于数列{ }，{ }，{ }，当时，。如果，{ }，{ }有相同的极限，那么数列{ }的极限存在，

证明：

对于任意给定的正数，可知存在正整数，，当时，成立，当时，成立。

取N=max{ ，，}，那么当时，和同时成立。

因此：。

所以：当时，成立。

2.函数，，在的某一领域内有定义，并且，存在正数，当不等式成立时，。如果当时，函数，有相同的极限，那么函数的极限存在，

证明：

对于任意给定的正数，可知存在正数，，当不等式成立时，成立，当不等式成立时，成立。

取=min{ ，，}，那么当不等式成立时，和同时成立。

因此：

所以：当不等式成立时，成立。

常数e存在定理2：

当时，

证明：

设，当时，。

函数

=

当时，

的极限为e。

设，当时，。

函数

=

当时，

的极限为e。

由于，，对于函数，当时，存在正数，当不等式成立时，存在。

根据夹逼定理，函数，当时，极限为e。

常数e存在定理3：

证明：

根据常数e存在定理2，可知常数e存在定理3正确。