多边形裁剪|Sutherland-Hodgman
此算法只能裁剪凸多边形
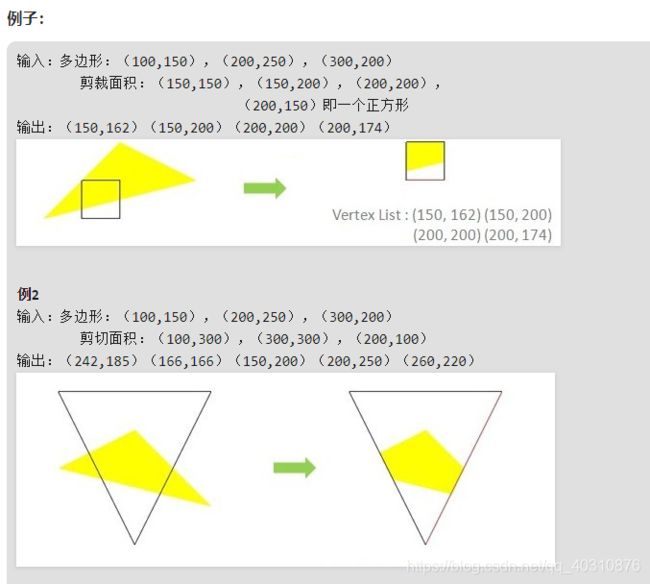
先看俩个例子
算法基本思想:
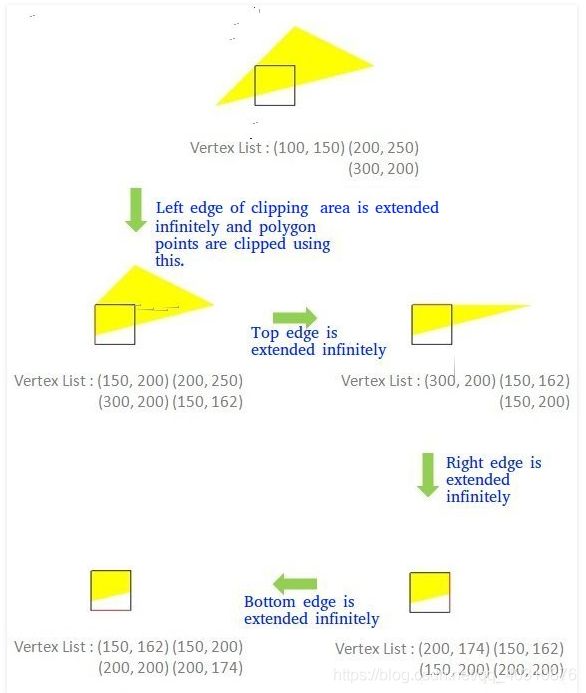
基本思想:一次用窗口的一条边来裁剪多边形。
算法的输入是以顶点序列表示的多边形,输出也是一个顶点序列,这些顶点能够构成一个或多个多边形。
处理对象:任意凸多边形。
窗口的任意一条边的所在直线(裁剪线)把窗口所在平面分成两部分:
可见一侧:包含窗口那部分
不可见一侧:不包含窗口那部分
l将每条线段的端点S, P与裁剪线比较之后,可以输出0~2个点:
(1) S, P都在可见一侧,输出顶点P。
(2) S, P都在不可见一侧,输出0个顶点。
(3) S在可见一侧,P在不可见一侧,输出SP与裁剪线的交点I。
(4) S在不可见一侧,P在可见一侧,输出SP与裁剪线的交点I和顶点P。
例如:
代码实现:
#include
using namespace std;
const int MAX_POINTS = 20;
//交点横坐标
int x_intersect(int x1, int y1, int x2, int y2,
int x3, int y3, int x4, int y4)
{
int num = (x1*y2 - y1*x2) * (x3-x4) -
(x1-x2) * (x3*y4 - y3*x4);
int den = (x1-x2) * (y3-y4) - (y1-y2) * (x3-x4);
return num/den;
}
//返回交点纵坐标
int y_intersect(int x1, int y1, int x2, int y2,
int x3, int y3, int x4, int y4)
{
int num = (x1*y2 - y1*x2) * (y3-y4) -
(y1-y2) * (x3*y4 - y3*x4);
int den = (x1-x2) * (y3-y4) - (y1-y2) * (x3-x4);
return num/den;
}
// 裁剪
void clip(int poly_points[][2], int &poly_size,
int x1, int y1, int x2, int y2)
{
int new_points[MAX_POINTS][2], new_poly_size = 0;
for (int i = 0; i < poly_size; i++)
{
int k = (i+1) % poly_size;
int ix = poly_points[i][0], iy = poly_points[i][1];
int kx = poly_points[k][0], ky = poly_points[k][1];
int i_pos = (x2-x1) * (iy-y1) - (y2-y1) * (ix-x1); //标志
int k_pos = (x2-x1) * (ky-y1) - (y2-y1) * (kx-x1);
// Case 1
if (i_pos < 0 && k_pos < 0)
{
new_points[new_poly_size][0] = kx;
new_points[new_poly_size][1] = ky;
new_poly_size++;
}
// Case 2
else if (i_pos >= 0 && k_pos < 0)
{
new_points[new_poly_size][0] = x_intersect(x1, y1, x2, y2, ix, iy, kx, ky);
new_points[new_poly_size][1] = y_intersect(x1, y1, x2, y2, ix, iy, kx, ky);
new_poly_size++;
new_points[new_poly_size][0] = kx;
new_points[new_poly_size][1] = ky;
new_poly_size++;
}
// Case 3
else if (i_pos < 0 && k_pos >= 0)
{
new_points[new_poly_size][0] = x_intersect(x1,y1, x2, y2, ix, iy, kx, ky);
new_points[new_poly_size][1] = y_intersect(x1,y1, x2, y2, ix, iy, kx, ky);
new_poly_size++;
}
// Case 4 不添加点
else
{
}
}
poly_size = new_poly_size;
for (int i = 0; i < poly_size; i++)
{
poly_points[i][0] = new_points[i][0];
poly_points[i][1] = new_points[i][1];
}
}
void suthHodgClip(int poly_points[][2], int poly_size,
int clipper_points[][2], int clipper_size)
{
for (int i=0; i 输出:
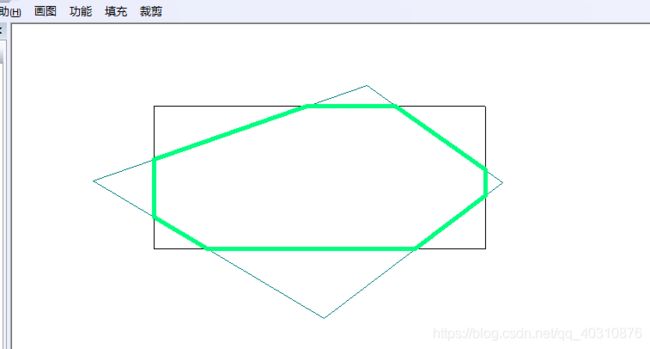
(150,162)(150,200)(200,200)(200,174)基于vs2010MFC实现
上图
其他图形学代码下载:https://download.csdn.net/download/qq_40310876/11222412
来源于中华女子学院山东分校赵晓峰的论文